РГЗ Теплотехника вариант 76. Теплотехника. Вар - 76. Решение Изотермический процесс (12)
 Скачать 266.01 Kb. Скачать 266.01 Kb.
|
|
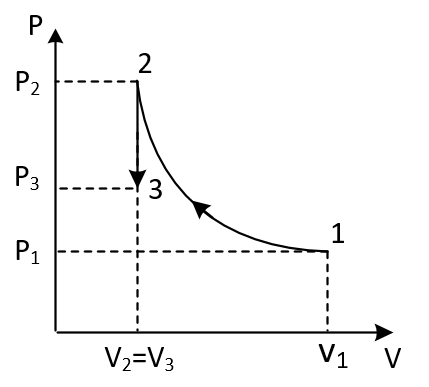
Министерство общего и профессионального образования Российской Федерации Красноярский Государственный Аграрный Университет Расчетная работа По дисциплине «Теплотехника» Вариант 76 Выполнил: студент Медведев Д. С. _________ Проверил: преподаватель Зыков С. А._____________ Красноярск 2022 Модуль 1. Техническая термодинамика Задание 1 Углекислый газ из начального состояния с параметрами р1 и t1 изотермически сжимается до давления р2, а затем изохорно охлаждается до температуры t3. Определить параметры состояния во всех остальных точках процессов и показать эти процессы в р,v и T,s–диаграммах. Вычислить также величины работы, теплоты, изменения внутренней энергии и энтропии в каждом процессе.
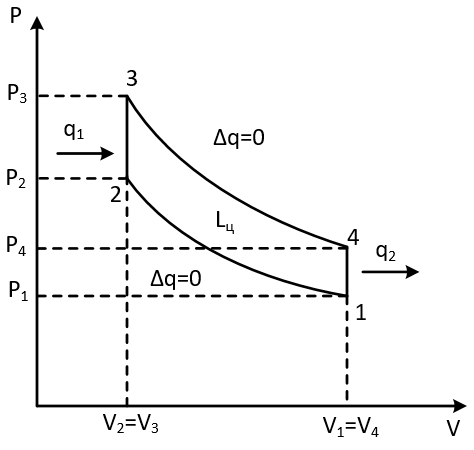
Решение: Изотермический процесс (1-2) Уравнение состояния идеального газа 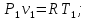 Значение газовой постоянной 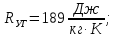 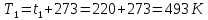 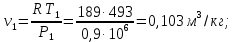 Зависимость между параметрами в изотермическом процессе  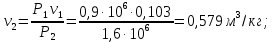 Определим работу в изотермическом процессе 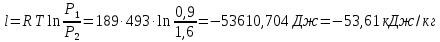 Первый закон термодинамики 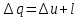 т.к. в изотермическом процессе 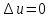 , то: , то:Изменение количества теплоты в изотермическом процессе 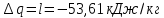 Изменение энтропии в изотермическом процессе 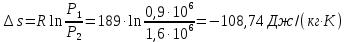 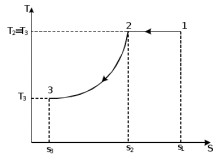 Изохорный процесс (2-3) Зависимость между параметрами в изохорном процессе 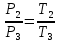  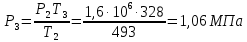 Изменение количества теплоты в изохорном процессе 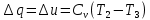 Значение удельная теплоемкость взято из таблицы [4] 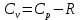 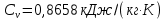 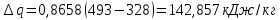 Изменение энтропии в изохорном процессе 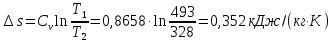 Задание 2 Рассчитать цикл теплового двигателя с максимальной температурой рабочего тела t3, в котором сжатие и расширение рабочего тела осуществляются по политропам с показателями n1 и n2 соответственно. Определить: параметры состояния рабочего тела в характерных точках цикла; подведенную и отведенную теплоту; работу цикла и его КПД; построить цикла в р,v–диаграмме. В качестве рабочего тела рассматривать воздух, зависимостью его теплоемкости от температуры – пренебречь.
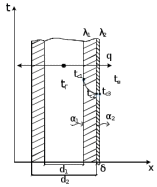
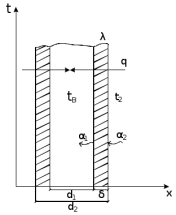
Решение: Расчет параметров состояния Точка 1: 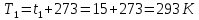 Значение газовой постоянной взято из табл ( 2) 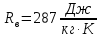 Уравнение состояния идеального газа 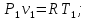 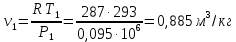 Точка 2: Степень сжатия 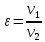 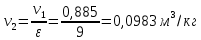 Давление из уравнения политропы pvn1 = const 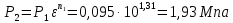 Температура в политропном процессе  Точка 3: Объем в изохорном процессе 1-2 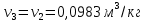 Абсолютная температура  Давление из уравнения состояния идеального газа  Точка 4: Объем в изохорном процессе 4-1  Давление из уравнения политропы pvn2 = const 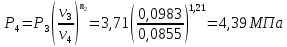 Температура из уравнения состояния идеального газа 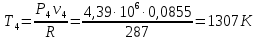 Расчет теплоты и работы Количество подведенного тепла  Уравнение Майера 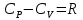 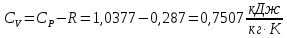 Количество отведённого тепла  Уравнение Майера 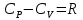 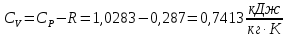 Показатель адиабаты воздуха 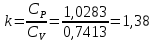 Термический КПД 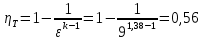 Работа цикла 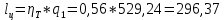 кДж кДжМодуль 2. Основы теории тепломассообменаЗадание 3 По стальной трубе, внутренний и внешний диаметры которой соответственно d1 и d2, и теплопроводность =40 Вт/(мК), течет газ со средней температурой tг; коэффициент теплоотдачи от газа к стенке 1. Снаружи труба охлаждается водой со средней температурой tв; коэффициент теплоотдачи от стенки к воде 2. Определить коэффициент теплопередачи k от газа к воде, тепловой поток q и температуры поверхностей трубы. Данные, необходимые для решения задачи, выбрать из табл. Определить также температуру внешней поверхности трубы и q, если она покрылась слоем накипи толщиной =2 мм, теплопроводность которой =0,8 Вт/(мК) (при 2=const).
Решение: Без накипи: Линейный коэффициент теплопередачи  Линейная плотность теплового потока 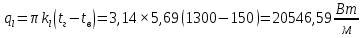 Закон Ньютона – Рихмана 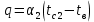 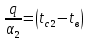 Определим температуру на наружной стенки 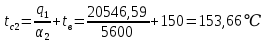 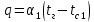 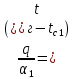 Определим температуру внутренней стенки 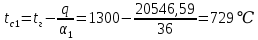 С накипью: Коэффициент теплопередачи  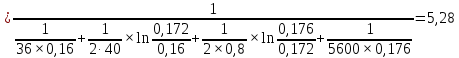 Плотность теплового потока 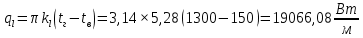 Закон Ньютона – Рихмана 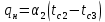 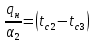 Определим температуру на наружной стенки с накипью 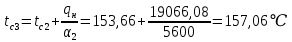 Задание 4Воздух течет внутри трубы, имея среднюю температуру tв, давление p=1МПа и скорость . Определить коэффициент теплоотдачи от трубы к воздуху 1, а так же удельный тепловой поток q, если внутренний диаметр трубы d1 , толщина её , и теплопроводность = 20 Вт/(м К). Температура и коэффициент теплоотдачи горячих газов, омывающих трубу, соответственно равны t2 и 2. Исходные данные представлены в табл. 4
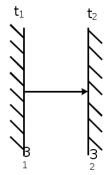
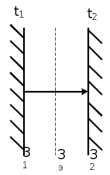
Решение: Определим d2:  Критерий Рейнольдса:  смотреть в таблице 7 смотреть в таблице 7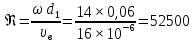 Так как 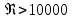 следовательно это турбулентный режим следовательно это турбулентный режим Коэффициент теплоотдачи от трубы к воздуху 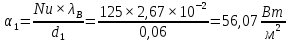 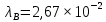 – теплопроводность воздуха – теплопроводность воздухаЛинейная плотность теплового потока: 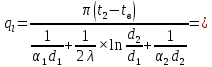 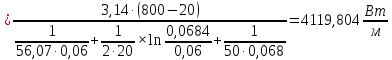 Задание 5 Определить удельный лучистый тепловой поток q между двумя параллельно расположенными плоскими стенками, имеющими температуру t1 и t2 и степени (коэффициенты) черноты 1 и 2, если между ними нет экрана. Определить q при наличии экрана со степенью (коэффициентом) черноты э (с обеих сторон). Исходные данные представлены в табл.5
Решение: Без экрана: Приведённая степень черноты 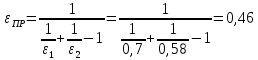 Поверхностная плотность теплового потока излечения 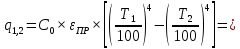 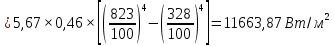  С экраном: Приведённая степень черноты 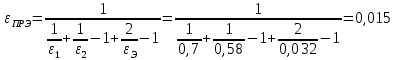 Поверхностная плотность теплового потока излечения 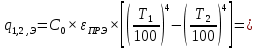 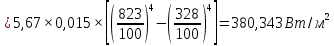 Задание 6Определить поверхность нагрева рекуперативного водовоздушного теплообменника при прямоточной и противоточной схемах движения теплоносителей, если объемный расход воздуха при нормальных условиях Vн, средний коэффициент теплопередачи от воздуха к воде k, начальные и конечные температуры воздуха и воды равны соответственно t1, t1, t2, t2. Определить также расход воды G через теплообменник. Исходные данные представлены в табл.6
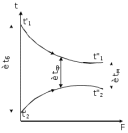
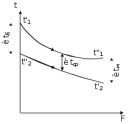
Решение: При прямоточной схеме Уравнение теплопередачи:  Уравнение теплового баланса 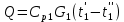 Cp1 = 1,059 кДж/(кгК) – изобарная теплоемкость воздуха 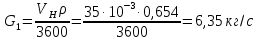 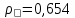 – плотность воздуха – плотность воздуха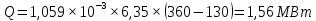 если, 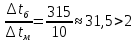 , то , то 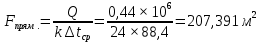 Определим расход воды G2  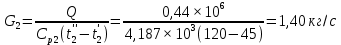 Cp2(70) = 4,187 кДж/(кгК) – изобарная теплоемкость воды При противоточной схеме Меняется только значение  если, 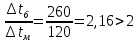 , то , то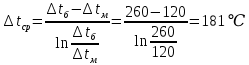 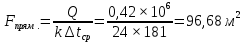 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||

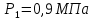

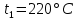
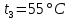
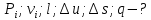
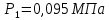
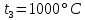
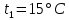
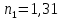
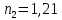
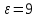
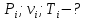
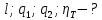
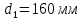
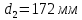
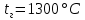
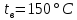
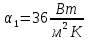
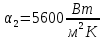
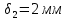
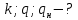
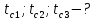
 10-3 м3/ч
10-3 м3/ч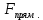 ;
;  ;
; 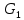 ;
; 