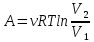Физика. ФИЗИКА. Решение кинетическая энергия Wk момент инерции j 400 кг м2 угловая скорость в момент времени t
 Скачать 58.55 Kb. Скачать 58.55 Kb.
|
|
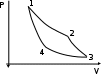
Покоившийся вначале маховик под действием постоянного вращающего момента за 10 с приобрел кинетическую энергию в 2 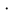 10–4 Дж. Определить, сколько оборотов совершил маховик за это время, если его момент инерции равен 10–4 Дж. Определить, сколько оборотов совершил маховик за это время, если его момент инерции равен  . .Дано: ω0 = 0; Wк = 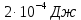 ; t = 10 с; J = 400 кг⋅м2. ; t = 10 с; J = 400 кг⋅м2.Найти: N-? Решение: кинетическая энергия Wk = 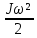 -----> ω = -----> ω = 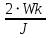 момент инерции J = 400 кг  м2 м2угловая скорость в момент времени t ω = ω0 + εt вначале маховик покоился ω0 = 0 -----> ω = εt угловое ускорение ε = 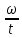 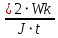 угол поворота в момент времени t φ = φ0  t + t + 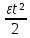 φ0 = 0 -----> φ = 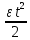 = = 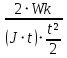 = = 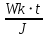 число оборотов совершил маховик за время t N = 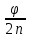 = = 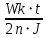 Подставим значения N = 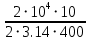 = 79,6 об = 79,6 обОтвет: 79,6 оборотов при условии Wк = 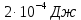 1.31. Тепловая машина Карно совершает работу с двумя молями одноатомного идеального газа между тепловым резервуаром с температурой 3270С и холодильником с температурой 270С. Отношение наибольшего объема газа к наименьшему объему в данном процессе равно восьми. Какую работу совершает машина за один цикл? Какое количество теплоты получает от нагревателя и отдает холодильнику? Чему равно изменение энтропии при изотермическом сжатии?
Запишем данную формулу для работ 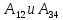 : :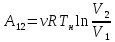 и и 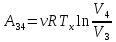 (2) (2)Работы 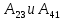 - это работы в адиабатном процессе. Формула работы для адиабатного процесса имеет вид: - это работы в адиабатном процессе. Формула работы для адиабатного процесса имеет вид: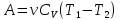 Запишем данную формулу для работ 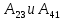 : :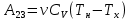 и и 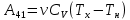 (3) (3)Подставим формулы (2) и (3) в формулу (1) 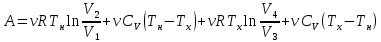 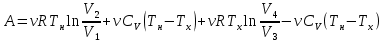 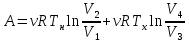 ………………………………….(4) ………………………………….(4)Уравнение адиабатного процесса имеет вид: 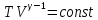 Запишем это уравнение для процессов 2-3 и 4-1 соответственно: 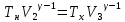 и и 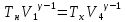 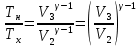 и и 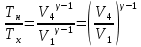 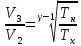 и и 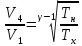 Выразим объемы V2 и V4: 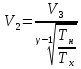 и и 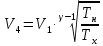 (5) (5)Подставим полученные выражения в формулу (4): 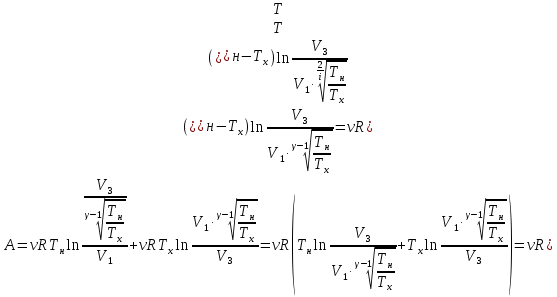 где γ – показатель адиабаты: 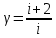 Размерность: 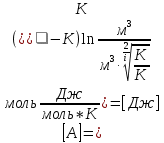 Расчет: 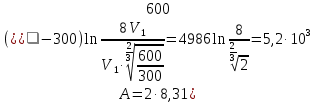 При адиабатном процессе теплообмена с окружающей средой не происходит (по определению адиабатного процесса). Значит передача теплоты осуществляется в данном случае только в изотермических процессах 1-2 и 3-4. От нагревателя тело получает тепло в процессе 1-2 – изотермическое расширение – теплота Qн, а отдает холодильнику в процессе 3-4 – изотермическое сжатие – теплота Qх. По первому началу термодинамики теплота определяется формулой: 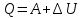 В изотермическом процессе ΔU=0, так как не происходит изменения температуры. Следовательно, для изотермического процесса: 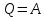 Тогда (как следует из рассуждений выше) получаем: 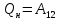 и и 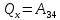 С учетом формул (2) и (5) получаем: 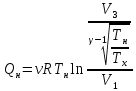 и и 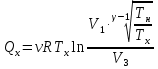 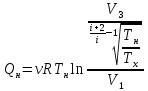 и и 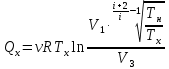 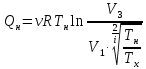 и и 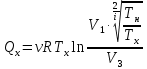 Размерность: 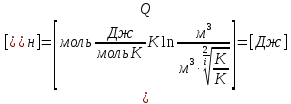 и и 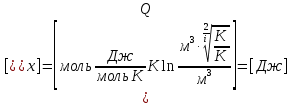 Расчет: 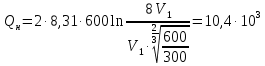 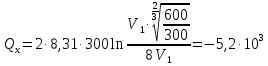 Знак «-» показывает, что тепло отдается системой. Изменение энтропии при изотермическом процессе определяется по формуле: 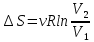 C учетом формулы (5) для процесса 3-4: 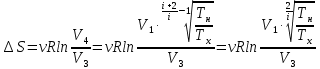 Размерность: 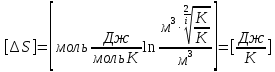 Расчет: 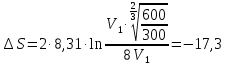 Ответ: А 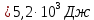 ; Qн ; Qн 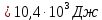 ; Qх ; Qх 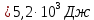 ; ΔS ; ΔS 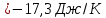 2.4. В элементарной теории атома водорода принимают, что электрон вращается вокруг протона по круговой орбите. Какова скорость вращения электрона, если радиус орбиты равен 0,53  10–10 м? 10–10 м?Дано: q=1,6 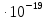 ; r= ; r=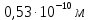 ; ; 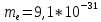 кг. кг.Найти: 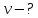 Решение: Сила электрического взаимодействия электрона с ядром (протоном) атома водорода определяется по закону Кулона 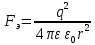 , ,Где q – заряд электрона и протона, r – радиус орбиты – расстояние между электроном и протоном, 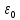 – электрическая постоянная. Центростремительная сила – электрическая постоянная. Центростремительная сила 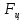 , определяющая вращение электрона по круговой орбите, имеет выражение , определяющая вращение электрона по круговой орбите, имеет выражение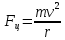 и численно равна силе электрического взаимодействия 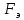 Приравнивая 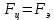 , получим , получим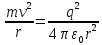 , ,откуда 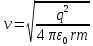 ; ;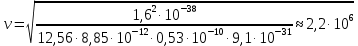 (м/с). (м/с).Ответ: 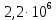 (м/с) скорость вращения электрона, при радиусе орбиты (м/с) скорость вращения электрона, при радиусе орбиты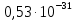 кг. кг.2.38. Какое напряжение можно дать на катушку, имеющую 1000 витков медного провода, со средним диаметром витков 6 см, если допустимая плотность тока – 2 А/мм2? Дано: N=1000 d=6 см= 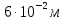 jдоп 2 А/мм2 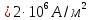 p=1,7 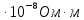 Найти: 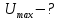 Решение: Плотность тока в проводнике равна: j 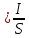 , ,где I – сила тока в проводнике; S – площадь поперечного сечения проводника. Сопротивление проводника равно: 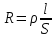 , ,где 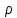 – удельное сопротивление материала проводника; – удельное сопротивление материала проводника;l – длина проводника. Разность потенциалов (напряжение), которое будет падать на катушке, по закону Ома равна: 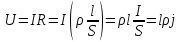 Длина одного витка 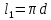 , ,где d – средний диаметр витка. Поскольку в катушке Nвитков, то длина медной проволоки, из которой сделана катушка, равна: 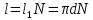 . .Таким образом, выражение для напряжения, падающего на катушке, примет вид:  Максимальное напряжение, которое можно дать на катушку, соответствует допустимой плотности тока: 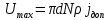 ; ;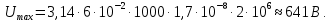 Ответ: 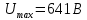 напряжения можно дать на катушку. напряжения можно дать на катушку.3.1. Рамка диаметром 6 см содержит 100 витков. Плоскость витков совпадает с направлением напряженности однородного магнитного поля, равной 15 А/м. Какой вращающий момент действует на рамку при силе тока в ней 10 А? Дано: d = 6 см = 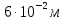 N = 100 H = 15 A/м I = 10 A Найти: M - ? Решение: На виток с током действует механический вращающий момент величиной: 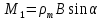 где 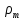 – магнитный момент витка; – магнитный момент витка;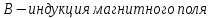 ; ;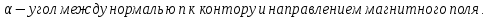 Сделаем рисунок согласно условию задачи. 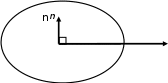 H, B Из рисунка следует: 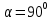 . .Магнитный момент плоского витка с током: 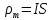 где I – сила тока в витке; S – площадь витка. Для круглого витка диаметром d: 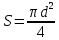 Следовательно: 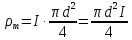 Напряженность Hи индукция Bодного и того же магнитного поля в немагнитной среде связаны соотношением: 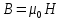 , ,Где 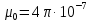 Гн/м – магнитная постоянная. Гн/м – магнитная постоянная.Итак, на один виток рамки в данном случае будет действовать вращающий момент: 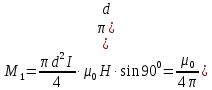 Тогда на рамку, содержащую N витков, будет действовать вращающий момент: 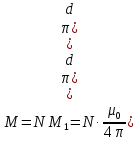 Выполним проверку размерности: 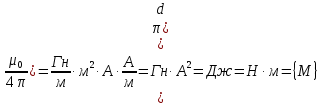 (верно) (верно)Проведем расчет: 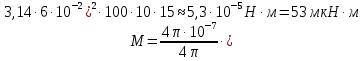 Ответ: М=53 мкН  м. м.3.36. В соленоиде без сердечника сила тока равномерно возрастает на 0,3 А/с. Число витков соленоида – 1100; площадь его поперечного сечения – 100 см2; длина – 60 см. На соленоид надето изолированное кольцо того же диаметра. Вычислить ЭДС индукции в кольце. |

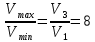
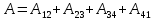 (1)
(1)