Решение контрольного задания. Решение контрольного задания По "правилу треугольника"
 Скачать 73.96 Kb. Скачать 73.96 Kb.
|
|
Решение контрольного задания 1. По "правилу треугольника" сложения векторов, учитывая, что  = =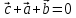 , получим : , получим :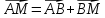 = =  = = 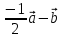 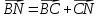 = =   = = 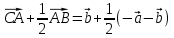 = =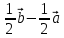  Рисунок 1 2. Проведем через вершину А прямую l параллельно BC (рис.2). Если D - середина BC , то 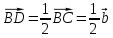 . Проведем AD и FB // AD , тогда AF=BD и . Проведем AD и FB // AD , тогда AF=BD и  . .Проведем CE // AB , тогда AE=BC и 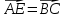 , следовательно , следовательно 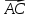 = =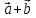 . Если P - середина АС, то . Если P - середина АС, то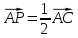 = = Далее, т.к. Далее, т.к. 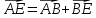 , то , то 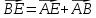 = =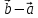 . Проведем FK до пересечения с продолжением стороны BC, тогда . Проведем FK до пересечения с продолжением стороны BC, тогда 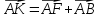 = = 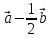 . . Вектор 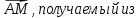 вектора вектора  его на 2, равен его на 2, равен  . И так : . И так : ; ; 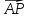 = = ; ; 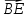 = =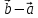 ; ;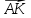 = = 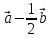 ; ; 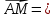  . .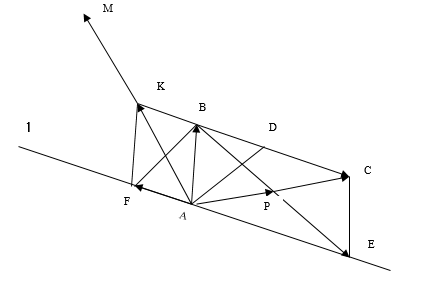 Рисунок 2 3. Рассмотрим два вектора 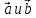 , приведенных к одному началу (рис.3): , приведенных к одному началу (рис.3):  ; ; 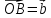 . . Рисунок 3 Построим на векторах 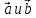 параллелограмм OACB. По определению сумы векторов имеем: параллелограмм OACB. По определению сумы векторов имеем: = =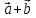 , ,  = =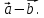 Если предположить, что векторы 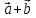 и и  ортогональны, то это означает перпендикулярность диагоналей параллелограмма, откуда следует, что параллелограмм OACB будет ромб. Итак, из условия ортогональности векторов ортогональны, то это означает перпендикулярность диагоналей параллелограмма, откуда следует, что параллелограмм OACB будет ромб. Итак, из условия ортогональности векторов 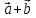 и и  следует, что векторы следует, что векторы 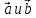 имеют равные длины. имеют равные длины.Предположим, что для векторов 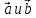 имеет место равенство: | имеет место равенство: |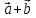 |=| |=|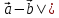 , т.е в параллелограмме, построенном на векторах , т.е в параллелограмме, построенном на векторах 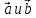 диагонали равны. Это означает, что OACB – прямоугольник. диагонали равны. Это означает, что OACB – прямоугольник.Итак, из условия  следует следует  , а из условия | , а из условия |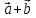 |=| |=|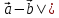 следует, что следует, что 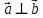 . Тогда одновременное выполнение обоих условий влечет иа собой | . Тогда одновременное выполнение обоих условий влечет иа собой | | = | | = | и и 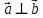 . .4. Рассмотрим параллелограмм ABCD (рис.4) и предположим, что точка О такова, что 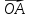 + +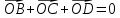 (1) (1) Рисунок 4 По правилу сложения векторов имеем:  = = = = ; ;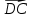 = =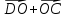 = =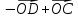 ; ;Так как противоположные стороны параллелограмма равны и параллельны, то 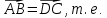  = =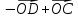 , или , или 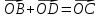 + +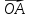 (2) (2)По предположению, точка О такова, что выполнено условие (1), тогда из (1), учитывая (2), получим 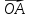 + + + +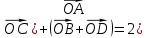 + +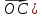 =0; =0;т.е. векторы 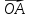 и и противоположные векторы. Это означает, что они лежат на одной прямой, равны по длине и противоположно направлены. Из сказанного следует, что точка О является серединой диагонали AC, т.е. является точкой пересечения диагоналей ACи BDпараллелограмма ABCD. Эта точка единственна. Проведенные рассуждения не требуют дополнительных рассмотрений, т.к. из предположения, что выполнено (1) с необходимостью вытекает, что точка О является точкой пересечения диагоналей, а эта точка единственна. противоположные векторы. Это означает, что они лежат на одной прямой, равны по длине и противоположно направлены. Из сказанного следует, что точка О является серединой диагонали AC, т.е. является точкой пересечения диагоналей ACи BDпараллелограмма ABCD. Эта точка единственна. Проведенные рассуждения не требуют дополнительных рассмотрений, т.к. из предположения, что выполнено (1) с необходимостью вытекает, что точка О является точкой пересечения диагоналей, а эта точка единственна.5. Угол между векторами  обозначим через φ, он находится по формуле обозначим через φ, он находится по формулеcos φ = 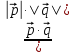 Если 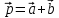 и и 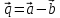 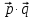 =( =(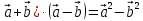 = 3 - 1 = 2 = 3 - 1 = 2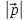 = =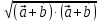 = =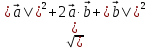 = =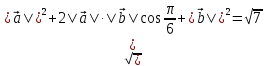 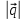 = =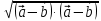 = =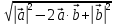 = = Таким образом cos φ = 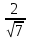 ; и φ = arсcos ; и φ = arсcos 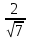 6. По определению, проекция вектора  на ось Ox определяется по формуле на ось Ox определяется по формуле = = 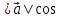 φ ; (1) φ ; (1)где φ – уголь между осью Ox и вектором  В рассматриваемом случае ось Ox параллельна вектору 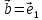 + + и противоположно ему направлена, т.е. направление оси Ox совпадет с направлением вектора и противоположно ему направлена, т.е. направление оси Ox совпадет с направлением вектора  . Уголь φ между векторами . Уголь φ между векторами 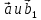 находится по формуле: находится по формуле:cos φ = 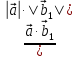 ; ;поставляя это в (1), получим:  = = 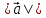 . . 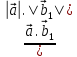 = = 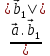 . .Находим скалярное произведение векторов  + + и и  ; ; и длину вектора 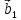 : | : |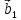 |= |=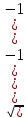 = =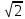 Таким образом:  = =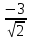 ; (Напомним, что через ; (Напомним, что через 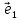 и и  мы обозначали единичные взаимно перпендикулярные векторы). мы обозначали единичные взаимно перпендикулярные векторы).7. По определению  = = =6 ; =6 ;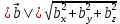 = = =7 ; =7 ;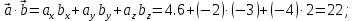 (2  )∙( )∙( ∙ ∙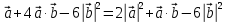 = ==2∙ 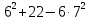 = - 200. = - 200.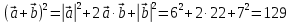 Если φ - уголь между векторами 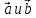 , то , тоcos φ = 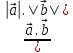 = =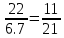 ; т.е. φ = arсcos ; т.е. φ = arсcos 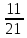 . .8. Если векторы 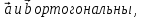 то их скалярное произведение равно нулю: то их скалярное произведение равно нулю: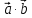 = (k = (k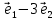 +2 +2 +2 +2 Откуда следует, что k= - 6. 9. Обозначим 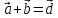 и найдем проекции вектора и найдем проекции вектора 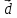 по оси кооринат: по оси кооринат: ; ;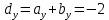 ; ;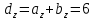 . .По определению 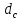 = = 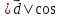 φ , где φ - уголь между векторами φ , где φ - уголь между векторами 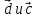 . Так как, cosφ = . Так как, cosφ = 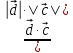 , то , то 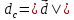 . . 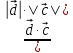 = =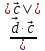 Находим   = =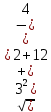 =13 ; =13 ;Откуда следует, что 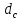 = =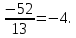 10. Предположим, что 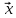 = = 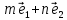 + + . .Если вектор 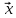 коллинеарен вектору коллинеарен вектору  = = 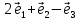 , то между векторами , то между векторами 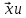  существует пропорциональность, т.е. существует пропорциональность, т.е.  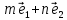 + + = = , ,или 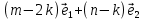 + + =0. =0.Вектор будет нулевым тогда и только тогда, когда все его проекции на оси координат равны нулю, т.е. 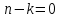 , , 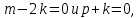 откуда следует, что откуда следует, что 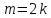 , , 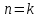 , , 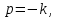 т.е. т.е. 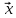 = =   . Найдем k на условии . Найдем k на условии 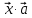 =3. =3.3= (  = = 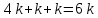 , ,Откуда  . . Таким образом, 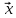 = =  . . |
