9 класс Текстовые задачи решение каждой задачи. 52 урок текстовые задачи. Решение которых требует составления уравнения, а также их систем на основании условия задачи

• Название: Решение которых требует составления уравнения, а также их систем на основании условия задачи
• Анкор: 9 класс Текстовые задачи решение каждой задачи
• Дата: 24.04.2022
• Размер: 0.99 Mb.
• Имя файла: 52 урок текстовые задачи.docx
• Тип: Задача; #492782

1. Задачи на движение.

В настоящее время на экзамене по математике в блоке “алгебра” предлагаются задачи, решение которых требует составления уравнения, а также их систем на основании условия задачи.

Указания к задачам:

1.Основными компонентами этого типа являются:

а) пройденный путь (S);

б) скорость (v);

в) время (t).

2. Зависимость между величинами выражается известными формулами:

S=v/t; v=S/t; t=S/v.(Указанные величины должны быть в одной системе единиц, например: путь в км, время в часах, то скорость в км/час.)

Задача 1.

Из А в В по течению реки отправился плот. А через час вслед за ним отправилась яхта, которая, прибыв в пункт В тотчас повернула обратно и возвратилась в А.  К этому времени  плот удалился от А на расстояние 24 км. Пристань А расположена в 120 км от пристани В. Найдите скорость яхты в неподвижной воде, если скорость течения реки равна 2 км/ч. Ответ дайте в км/ч.

1. Заполните таблицу.

	S (км)	v (км/ч)	t (ч)
Плот
Яхта (по течению)
Яхта (против течения)

Учитель математики. Анализируя текст с позиций русского языка, мы определили последовательность действий, а также сделали акценты в следующих аспектах:

• 
  время движения плота (“к этому времени”),
  
• 
  путь, который прошла яхта по течению и против течения (основа предложения “пристань расположена”),
  
• 
  характер движения по (против) течения (придаточное условия),
  
• 
  объект, который двигался в обе стороны (относительное местоимение “которая”),
  
• 
  направление, в котором двигалась яхта, достигнув пункта В (слово “обратно”).  
  

	S (км)	v (км/ч)	t (ч)
Плот	120	2	60
Яхта (по течению)	120	Х+2	120/х+2
Яхта (против течения)	120	Х-2	120/х-2

2. Составим и решим уравнение:

120/х+2+120/х-2=11 /*(х²-4)

11х²-240х-44=0

Д=240*240-4*11*(-44)=59536

Х₁= (240+244)/22=22; х₂ = (240-244)/22=-4/22 – не удовлетворяет условию задачи.

Ответ: 22 км/час.

Задача 2.

Пристани А и В расположены на реке, скорость течения которой на этом участке равна 4 км/ч. Лодка проходит от А до В и обратно без остановок со средней скоростью 6 км/ч. Найти собственную скорость лодки.

Решение:

Пусть х км/ч – собственная скорость лодки.

Лодка	V км/ч	tчас	Sкм
Из А в В	x-4	S/x-4	S
Из В в А	X+4	S/x+4	S

Составим уравнение:

(S/x-4 + S/x+4)*6=2 S.



Получим х=8 км/ч или х=-2(не удовлетворяет условию задачи)

Ответ: 8 км/час.

Теплоход проходит по течению реки до пункта назначения 80 км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода в неподвижной воде, если скорость течения равна 5 км/ч, стоянка длится 23 часа, а в пункт отправления теплоход возвращается через 35 часов после отплытия из него.

Решение.

Обозначим через x км/ч скорость теплохода в неподвижной воде. Тогда, его скорость по течению равна x+5 км/ч, а против течения x-5 км/ч. Сначала теплоход идет по течению реки 80 км, на которые он затратил   часов. З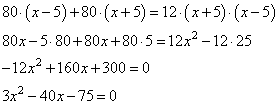атем, он стоит 23 часа, после чего движется в обратном направлении   часов. В сумме он затратил на весь путь 35 часов. Получаем уравнение:



откуда



Решаем квадратное уравнение, получаем два корня:

Так как скорость теплохода не может быть отрицательным числом, то получаем ответ 15 км/ч.

Ответ: 15.

2.Теплоход проходит по течению реки до пункта назначения 210 км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода в неподвижной воде, если скорость течения равна 24 км/ч, стоянка длится 9 часов, а в пункт отправления теплоход возвращается через 27 часов после отплытия из него.

Решение.

На путь теплоход тратит 27-9=18 часов
пусть х скорость теплохода , тогда скорость по течению (х+4) км /ч
против течения (х-4)км/ч

210/(х+4)  + 210/(х-4)=18

210*(х-4) +210*(х+4)=18*(х+4)(х-4)

210х-(210*4)+210х+(210*4)=18х²- 288

18х²-420х- 288 =0 сократим на 6

3х²-70х- 48=0

D=4900+576 =5476         √D=74

x=(70+74)/6= 24

x=(70-74)/6=-2/3 не подходит 

Ответ : 24 км/ч

3.Моторная лодка прошла против течения реки 208 км и вернулась в пункт отправления , затратив на обратный путь на 5 часов меньше , чем на путь против течения . Найдите скорость лодки в неподвижной воде , если скорость течения реки равна 5 км / ч

Решение.

Пусть х км/ч скорость лодки в неподвижной воде, тогда (х+5)км/ч - скорость лодки по течению реки, (х-5)км/ч - скорость лодки против течения реки. 208/(х+5)ч-время, затраченное на путь по течению реки, 208/(х-5)ч время, затраченное на путь против течения реки. По условию задачи, лодка на путь по течению затратила 5 меньше, чем на путь против течение реки, значит :

208/(х-5)-208/(х+5)=5
208*(х+5)-208*(х-5)=5*(х-5)*(х+5)
х≠-5, х≠5
208х+1040-208х+1040=5х²-125
5х²=1040+1040+125
5х²=2205
х²=441
х=21и х=-21-не удовл.
21км/ч - скорость лодки в неподвижной воде 
Ответ: 21км/ч

4.Моторная лодка прошла против течения реки 132км и вернулась в пункт отправления , затратив на обратный путь на 5 часов меньше,чем на путь против течения . Найдите скорость лодки в неподвижной воде ,если скорость течения реки равна 5км/ч.

Решение.

Пусть скорость лодки х км/ч. - против течения будет х-5. а по течению х+5
по условию 
132/(х-5)-132/(х+5)=5
решаем уравнение
(132*(х+5)-132*(х-5))/(х-5)(х+5)=5
(132х+660-132х+660)/( х²-25)=5
1320/( х²-25)=5
х²-25=1320:5
х²=264+25
х²=289

х=17и х=-17-не удовл.


х=17 км/ч - искомая скорость лодки
Ответ: 17 км/ч

6. Два велосипедиста одновременно отправляются в пробег протяжённостью 208 км. Первый едет со скоростью на 3 км/ч большей, чем второй, и прибывает к финишу на 3 часа раньше второго. Найдите скорость велосипедиста, пришедшего к финишу вторым.

Решение.

Обозначим через x км/ч скорость первого велосипедиста. Тогда скорость второго будет равна x-3 км/ч. Путь в 208 км первый проходит за   часов, а 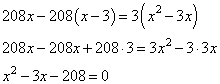второй за   часов. Известно, что разница во времени прибытия на финиш составляет 3 часа. Получаем уравнение:

,

откуда



Решаем квадратное уравнение, получаем: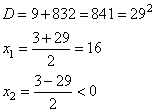



Имеем одно положительное значение x=16 км/ч. Это скорость первого велосипедиста. Скорость второго равна 16-3=13 км/ч.

Ответ: 13.

7.Расстояние между поселками А и Б 35 км два велосепидиста одновременно выезжают из А в Б первый едет со скоростью на 7 км в час больше чем второй найдите скорость второго велосипедиста если он приезжает в Б на 50 мин позже первого велосипедиста.

Решение.

второй велосипедист едет со скоростью х км/ч
Тогда первый со скоростью х+7 км/ч

50 минут =50/60 часа=5/6 часа

первый велосипедист ехал 35/(x+7) часов, а второй 35/x часов

составляем уравнение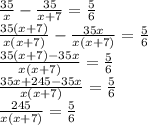




5x(x+7)=6*245

x(x+7)=294

x²+7x-294=0

D=7²+4*294=1225

√D=35

x₁=(-7-35)/2=-21 отбрасываем посторонний корень

x₂=(-7+35)/2=14 км/ч Ответ 14

Задача 1.

Из А в В по течению реки отправился плот. А через час вслед за ним отправилась яхта, которая, прибыв в пункт В тотчас повернула обратно и возвратилась в А.  К этому времени  плот удалился от А на расстояние 24 км. Пристань А расположена в 120 км от пристани В. Найдите скорость яхты в неподвижной воде, если скорость течения реки равна 2 км/ч. Ответ дайте в км/ч.

Задача 2.

Пристани А и В расположены на реке, скорость течения которой на этом участке равна 4 км/ч. Лодка проходит от А до В и обратно без остановок со средней скоростью 6 км/ч. Найти собственную скорость лодки.

Теплоход проходит по течению реки до пункта назначения 80 км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода в неподвижной воде, если скорость течения равна 5 км/ч, стоянка длится 23 часа, а в пункт отправления теплоход возвращается через 35 часов после отплытия из него.

2.Теплоход проходит по течению реки до пункта назначения 210 км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода в неподвижной воде, если скорость течения равна 24 км/ч, стоянка длится 9 часов, а в пункт отправления теплоход возвращается через 27 часов после отплытия из него.

3.Моторная лодка прошла против течения реки 208 км и вернулась в пункт отправления , затратив на обратный путь на 5 часов меньше , чем на путь против течения . Найдите скорость лодки в неподвижной воде , если скорость течения реки равна 5 км / ч

4.Моторная лодка прошла против течения реки 132км и вернулась в пункт отправления , затратив на обратный путь на 5 часов меньше,чем на путь против течения . Найдите скорость лодки в неподвижной воде ,если скорость течения реки равна 5км/ч.

6. Два велосипедиста одновременно отправляются в пробег протяжённостью 208 км. Первый едет со скоростью на 3 км/ч большей, чем второй, и прибывает к финишу на 3 часа раньше второго. Найдите скорость велосипедиста, пришедшего к финишу вторым.

7.Расстояние между поселками А и Б 35 км два велосепидиста одновременно выезжают из А в Б первый едет со скоростью на 7 км в час больше чем второй найдите скорость второго велосипедиста если он приезжает в Б на 50 мин позже первого велосипедиста.
Задача 1.

Из А в В по течению реки отправился плот. А через час вслед за ним отправилась яхта, которая, прибыв в пункт В тотчас повернула обратно и возвратилась в А.  К этому времени  плот удалился от А на расстояние 24 км. Пристань А расположена в 120 км от пристани В. Найдите скорость яхты в неподвижной воде, если скорость течения реки равна 2 км/ч. Ответ дайте в км/ч.

Задача 2.

Пристани А и В расположены на реке, скорость течения которой на этом участке равна 4 км/ч. Лодка проходит от А до В и обратно без остановок со средней скоростью 6 км/ч. Найти собственную скорость лодки.

Теплоход проходит по течению реки до пункта назначения 80 км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода в неподвижной воде, если скорость течения равна 5 км/ч, стоянка длится 23 часа, а в пункт отправления теплоход возвращается через 35 часов после отплытия из него.

2.Теплоход проходит по течению реки до пункта назначения 210 км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода в неподвижной воде, если скорость течения равна 24 км/ч, стоянка длится 9 часов, а в пункт отправления теплоход возвращается через 27 часов после отплытия из него.

3.Моторная лодка прошла против течения реки 208 км и вернулась в пункт отправления , затратив на обратный путь на 5 часов меньше , чем на путь против течения . Найдите скорость лодки в неподвижной воде , если скорость течения реки равна 5 км / ч

4.Моторная лодка прошла против течения реки 132км и вернулась в пункт отправления , затратив на обратный путь на 5 часов меньше,чем на путь против течения . Найдите скорость лодки в неподвижной воде ,если скорость течения реки равна 5км/ч.

6. Два велосипедиста одновременно отправляются в пробег протяжённостью 208 км. Первый едет со скоростью на 3 км/ч большей, чем второй, и прибывает к финишу на 3 часа раньше второго. Найдите скорость велосипедиста, пришедшего к финишу вторым.

7.Расстояние между поселками А и Б 35 км два велосепидиста одновременно выезжают из А в Б первый едет со скоростью на 7 км в час больше чем второй найдите скорость второго велосипедиста если он приезжает в Б на 50 мин позже первого велосипедиста.