Решение краевой задачи Требуется решить следующую задачу найти функцию u ( x ), x (0, l ), такую, что u (x) f (x), x (0, l), (1) u (0)
 Скачать 139.41 Kb. Скачать 139.41 Kb.
|
2. Решение краевой задачиТребуется решить следующую задачу: найти функцию u(x), x∈ (0, l), такую, что −u′(x) = f (x), x∈ (0, l), (1) u (0) = 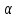 , u(l) = , u(l) = 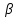 , ,где 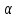 и и 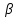 – заданные числа, а f (x) – заданная функция. – заданные числа, а f (x) – заданная функция. Интегрируя дифференциальное уравнение задачи (1) по отрезку [0, x], получим u′(x)= - 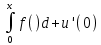 . .Интегрируя это соотношение по отрезку [0, x], выводим u(x)= - 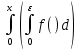 d d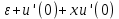 Преобразуем двойной интеграл из последнего соотношения: 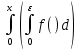 d d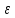 = = 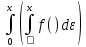 d d = = 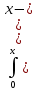 Таким образом, общее решение дифференциального уравнения задачи (1) имеет вид: x u(x) =- 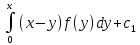 +xc2, (2) +xc2, (2)Определим постоянные c1 и c2 из граничных условий задачи (1): c1=a, c2= 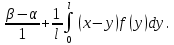 Подставляя постоянные c1 и c2 в соотношение (2), выводим u(x) =α+ 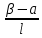 + +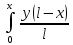 f (y) dy+ f (y) dy+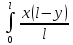 f (y) dy. f (y) dy.Итак, доказан следующий результат. Теорема 2. Решение задачи (1) определяется формулой: u(x)= =α+ 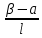 + +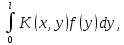 где 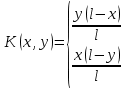 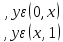 для x∈ (0, l). 3. Решение системы линейных уравнений Требуется решить систему линейных алгебраических уравнений n-го порядка следующего вида 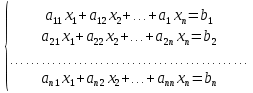 Здесь a11, a12, …, ann, b1, b2, …, bn – заданные коэффициенты и правые части, x1, x2, …, xn – неизвестные системы уравнений. Обозначим через x вектор неизвестных, через b – вектор правых частей, через A – матрицу коэффициентов: A = 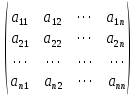 , x= , x= , b= , b=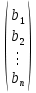 . .Тогда исходная система принимает вид Ax = b. (3) Положим ∆=det A и введем определитель ∆ j, получаемый из определителя ∆ заменой j-го столбца на столбец b правых частей системы уравнений, j =1, 2, ..., n. Теорема 3. (Правило Крамера) Если 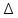 ≠ 0, то система (3) имеет единственное решение ≠ 0, то система (3) имеет единственное решение x1= 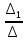 , x2= , x2= 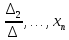 = =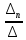 Если ∆= 0, а хотя бы один из определителей 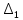 , , 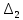 , …, , …, 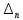 не равен нулю, то система (3) несовместна. не равен нулю, то система (3) несовместна. Если 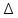 = = 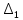 = = 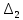 = ... = = ... = 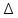 n = 0, то система (3) имеет бесконечно много решений. n = 0, то система (3) имеет бесконечно много решений. В качестве примера решим систему 3-го порядка 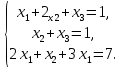 Непосредственные вычисления дают ∆ =  =4, ∆1 = =4, ∆1 =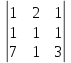 =4, ∆2 = =4, ∆2 =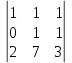 =-4, ∆3 = =-4, ∆3 =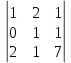 =8. =8.Применяя правило Крамера, находим x1 = 4/4 =1, x2 = (−4)/4 = −1, x3 = 8/4 = 2. 4. Вычисления 4.1. Нахождение частного 425/25=17 1/3 = 0,33333333333333333333333333333333 π/2 =1,5707963267948966192313216916398 4.2. Извлечение квадратного корня 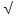 225 =15 225 =15 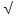 3 =1,7320508075688772935274463415059 3 =1,7320508075688772935274463415059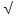 π=1,7724538509055160272981674833411 π=1,7724538509055160272981674833411 4.3. Вычисление процентов 50% от 90 = 45 25% от 3 = 0,75 30% от 150 = 45 4.4. Возведение в степень 33 =27 25 =32 210 =1024 4.5. Длина окружности радиуса R = 3: 2πR =18,849555921538759430775860299677 4.6. Площадь круга радиуса R = 3: πR2 = 28,274333882308139146163790449516 4.7. Выражения 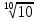 =1,2589254117941672104239541063958 =1,2589254117941672104239541063958 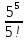 = 26,041666666666666666666666666667 = 26,041666666666666666666666666667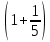 5 = 2,48832 5 = 2,48832С  труна, нагруженная массами труна, нагруженная массамиВнутренний элемент струны  Элемент струны с грузом  Вычисление суммы двух целых чисел  Решение линейного уравнения ax +b=c  Начало                     конец да Ввод a, b, с X=(c-b)/2 нет а=0 b=c нет реш. нет Любое число да  Вывод, x Вычисление конечной суммы  начало                 конец S=0; n=10; i=0 S=s+I/i i<=n Вывод s Нет Да I=i+1 Вычисление бесконечной суммы  начало   S=0; eps: =1E-3;i=0   i: =i+1     a: =1/i/i; s=s+a    нет (abs (a)   да  Вывод, s   конец К морю Прощай свободная стихия! В последний раз передо мной Ты катишь волны голубые И блещешь гордою красой. Как друга ропот заунывный, Как зов его в прощальный час, Твой грустный шум, твой шум призывный Услышал я в последний раз. А.С. Пушкин |
