открытый урок решение квадратных уравнений с применением теоремы виета. Решение квадратных уравнений с применением теоремы Виета. Решение квадратных уравнений с применением теоремы Виета

• Название: Решение квадратных уравнений с применением теоремы Виета
• Анкор: открытый урок решение квадратных уравнений с применением теоремы виета
• Дата: 10.04.2022
• Размер: 47.66 Kb.
• Имя файла: Решение квадратных уравнений с применением теоремы Виета.docx
• Тип: Решение; #460403

Решение квадратных уравнений с применением теоремы Виета

Цель: Применение теоремы Виета и ей обратной теоремы при нахождении коэффициентов в квадратных уравнениях, при решении заданий из вариантов ЕГЭ.

Воспитательные задачи: Способствовать формированию умений, применять приемы сравнений, обобщения, выделения главного, переноса знаний в новую ситуацию, развитию творческих способностей. Побуждать учащихся к самоконтролю и взаимоконтролю, самоанализу своей учебной деятельности.

Оборудование: плакаты, компьютер, экран, видеопроектор.

Ход урока

I. Вводная беседа. Устные упражнения (5 мин.)

Сегодня на уроке мы с вами вместе подведем итог, как важно применение теоремы Виета. В каких упражнениях применяется теорема и как важно ее знать и применять. (Учитель показывает презентацию, в которой сформулированы цели, задачи, структура урока). <Приложение 1>

Учащиеся формулируют теорему Виета и ей обратную теорему. У доски два ученика записывают формулы теоремы Виета для приведенного и полного квадратных уравнений:

 – формулы для полного квадратного уравнения;

 – формулы для приведенного квадратного уравнения;

Трое учащихся решают на дополнительных досках индивидуальные задания.

Решите уравнения и выполните проверку по теореме, обратной теореме Виета: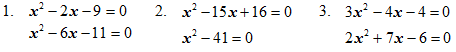



II. Устные упражнения (5 мин.)

Затем с учащимися решаем устные упражнения:

Найдите корни уравнения: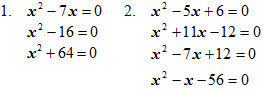



3. Если в квадратном уравнении сумма коэффициентов a + b + c = 0,

То   Используя это свойство, решите уравнения:



4. Теорема Виета применяется при нахождении суммы и произведения корней. Покажите, как это выглядит. Перед вами уравнения:



У какого из данных уравнений:

1. 
   Сумма корней равна 6, а произведение – 16?
   
2. 
   Корни равны?
   
3. 
   Один из корней уравнения равен 6?
   
4. 
   Каждый из корней на 2 больше, чем корни уравнения  ? Ответ обосновать.
   

III. Лабораторная работа (3 мин.)

Учащимся предлагается выполнить лабораторную работу.

Составьте квадратные уравнения, которые:

• 
  не имеют корней;
  
• 
  имеет один из корней, равный 0;
  
• 
  имеет два корня, равных по модулю, но противоположных по знаку;
  
• 
  имело бы один корень;
  
• 
  сумма коэффициентов уравнения равна 0.
  

Учащиеся выполняют это задание по группам (4–5 учащихся в группе).

Пример лабораторной работы: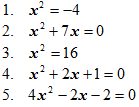



IV. Работа с таблицей (3 мин.)

Выполнив лабораторную работу, три группы озвучивают свою лабораторную работу, а остальные группы сдают лабораторные работы на плакатах на проверку (2 мин.).

Один из учащихся (Евсеев А.) заранее готовит презентацию об исследовании знаков в приведенных квадратных уравнениях. <Приложение 2>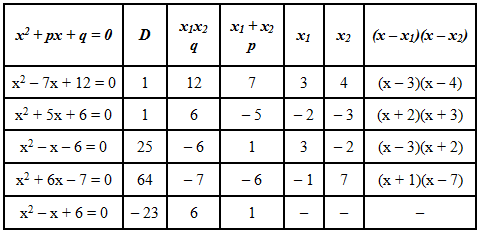



Все учащиеся работают с таблицей и отвечают на вопросы о знаках в квадратных уравнениях:

1. 
   Когда корни квадратного уравнения имеют одинаковые знаки?
   
2. 
   Когда оба корня положительные, отрицательные?
   
3. 
   Когда корни имеют разные знаки?
   
4. 
   Когда больший по модулю корень отрицателен?
   
5. 
   Когда больший по модулю корень положителен?
   

Сформулируйте выводы о знаках корней квадратных уравнений.

V. Тренировочные упражнения. Работа у доски (23 мин.)

Следующий этап урока: двое учащихся решают у доски задания о нахождении неизвестных коэффициентов в квадратных уравнениях.

1. В уравнении   один из корней равен 7. Найдите другой корень и коэффициент р. Ответ: 

2. Один из корней уравнения   равен 12,5. Найдите другой корень уравнения и коэффициент с. Ответ: 

Такого вида уравнения часто встречаются на экзаменах. Поэтому сейчас Слинько В. предлагает просмотреть презентацию о нахождении коэффициентов в квадратных уравнениях. <Приложение 3>

А после просмотра презентации учащимся предлагается решить 2 уравнения самостоятельно с последующей проверкой.

1. Разность корней квадратного уравнения   равна 2. Найдите с.

Ответ: c = 35.

2. Разность корней квадратного уравнения   равна 6. Найдите с.

Ответ: c = –8,75.

Использование теоремы Виета дает возможность решать более сложные задания.

Трое учащихся решают задания у доски, комментируя и объясняя ход решения:

1. Один из корней уравнения   равен 8. Найдите другой корень и коэффициент в.

Ответ:  .

2. Один из корней уравнения   равен 5,3. Найдите другой корень и коэффициент с.

Ответ:  .

3. В уравнении   квадратов корней равна  . Найдите с. Ответ: с = 9.

VI. Заключение (6 мин.)

В заключение урока подводим итоги. Учащиеся формулируют применение теоремы Виета.

Теорема Виета применяется:

• 
  при нахождении суммы и произведения корней квадратных уравнений;
  
• 
  при составлении квадратных уравнений;
  
• 
  при решении уравнений методом подбора;
  
• 
  при нахождении коэффициентов в уравнении, свободного члена;
  
• 
  при сравнении знаков коэффициентов в квадратном уравнении.
  

Один из учащихся рассказывает стихотворение.

По праву достойна в стихах быть воспета
О свойстве корней теорема Виета.
Что проще скажи постоянства такого?
Умножишь ты корни и дробь уж готова!
В числителе с, в знаменателе а,
А сумма корней тоже дроби равна.
Хоть с минусом дробь эта – что за беда?!
В числителе в, в знаменателе а.

Домашнее задание: № 645, № 667, № 671 из учебника «Алгебра 8», автор Макарычев Ю. Н.

Учитель выставляет оценки за урок, благодарит учащихся за работу на уроке.

Также предлагается посмотреть презентацию о решении квадратных уравнений с параметром, в которой рассматриваются задания повышенной сложности, применяемые на экзаменах и малом ЕГЭ. <Приложение 4>