Математика ,практ 2 осэк. Пр-1,математика. Решение Методом Крамера Воспользуемся формулой для вычисления определителя матрицы 33
 Скачать 17.47 Kb. Скачать 17.47 Kb.
|
|
Задание №1. Решить систему линейных уравнений методом Гаусса и методом Крамера: 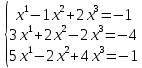 Решение: Методом Крамера: Воспользуемся формулой для вычисления определителя матрицы 3×3: ∆ = 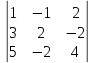 ∆ = 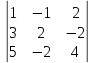 = 1·2·4 + (-1)·(-2)·5 + 2·3·(-2) - 2·2·5 - 1·(-2)·(-2) - (-1)·3·4 = 8 + 10 - 12 - 20 - 4 + 12 = -6 = 1·2·4 + (-1)·(-2)·5 + 2·3·(-2) - 2·2·5 - 1·(-2)·(-2) - (-1)·3·4 = 8 + 10 - 12 - 20 - 4 + 12 = -6∆1 = 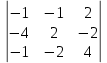 ∆1 = 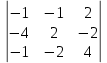 =(-1)·2·4 + (-1)·(-2)·(-1) + 2·(-4)·(-2) - 2·2·(-1) - (-1)·(-2)·(-2) - (-1)·(-4)·4 = -8 - 2 + 16 + 4 + 4 - 16 = -2 =(-1)·2·4 + (-1)·(-2)·(-1) + 2·(-4)·(-2) - 2·2·(-1) - (-1)·(-2)·(-2) - (-1)·(-4)·4 = -8 - 2 + 16 + 4 + 4 - 16 = -2∆2= 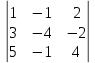 ∆2= 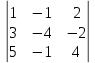 =1·(-4)·4 + (-1)·(-2)·5 + 2·3·(-1) - 2·(-4)·5 - 1·(-2)·(-1) - (-1)·3·4 = -16 + 10 - 6 + 40 - 2 + 12 = 38 =1·(-4)·4 + (-1)·(-2)·5 + 2·3·(-1) - 2·(-4)·5 - 1·(-2)·(-1) - (-1)·3·4 = -16 + 10 - 6 + 40 - 2 + 12 = 38∆3= 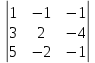 ∆3= 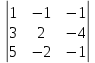 =1·2·(-1) + (-1)·(-4)·5 + (-1)·3·(-2) - (-1)·2·5 - 1·(-4)·(-2) - (-1)·3·(-1) = -2 + 20 + 6 + 10 - 8 - 3 = 23 =1·2·(-1) + (-1)·(-4)·5 + (-1)·3·(-2) - (-1)·2·5 - 1·(-4)·(-2) - (-1)·3·(-1) = -2 + 20 + 6 + 10 - 8 - 3 = 23Х1= 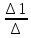 = =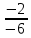 = =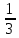 Х2= 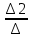 = =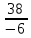 = =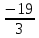 =-6 =-6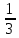 Х3= 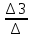 = =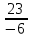 =- =- 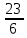 =-3 =-3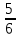 Методом Гаусса: 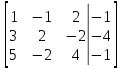 от 2 строки отнимаем 1 строку, умноженную на 3; от 3 строки отнимаем 1 строку, умноженную на 5: 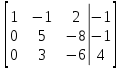 2-ую строку делим на 5: 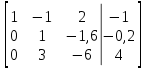 к 1 строке добавляем 2 строку, умноженную на 1; от 3 строки отнимаем 2 строку, умноженную на 3: 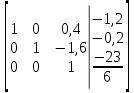 от 1 строки отнимаем 3 строку, умноженную на 0.4; к 2 строке добавляем 3 строку, умноженную на 1.6: 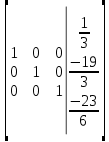 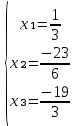 Сделаем проверку. Подставим полученное решение в уравнения из системы и выполним вычисления: 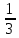 — — 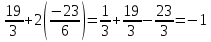 3 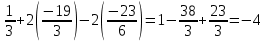 5 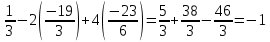 Проверка выполнена успешно. Ответ: 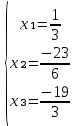 Задание №2. Решить систему линейных уравнений. 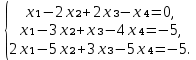 Решение: Из 1-ого уравнения выразим x₁ через остальные переменные: 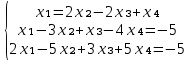 Во 2, 3 уравнение подставляем х₁ : 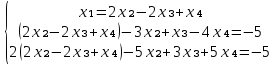 После упрощения получим: 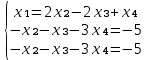 Поделим 2-ое уравнение на -1 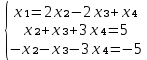 Из 2-ого уравнения выразим x2 через остальные переменные 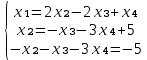 В 3 уравнение подставляем x₂ 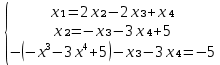 после упрощения получим: 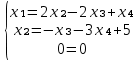 Ответ: 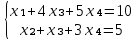 |
