Решение момент инерции стержня равен с учетом имеем Момент инерции диска относительно точки С
 Скачать 220.25 Kb. Скачать 220.25 Kb.
|
|
38.1. Н 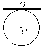 а одну плоскость положили тонкий однородный стержень массы mи длины l = 2R и диск радиуса Rи такой же массы m. Центр стержня О приварили к диску. Через точку О перпендикулярно плоскости получившейся детали проходит ось. Найти момент инерции детали относительно этой оси. m= 3 кг, R = 4 м. а одну плоскость положили тонкий однородный стержень массы mи длины l = 2R и диск радиуса Rи такой же массы m. Центр стержня О приварили к диску. Через точку О перпендикулярно плоскости получившейся детали проходит ось. Найти момент инерции детали относительно этой оси. m= 3 кг, R = 4 м.а) 48 кгм2; б) 68 кгм2; в) 88 кгм2; г) 108 кгм2; д) 128 кгм2. Решение: момент инерции стержня равен 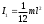 с учетом с учетом 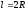 имеем имеем 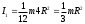 Момент инерции диска относительно точки С 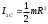 За теоремой Штейнера момент инерции относительно точки О равен 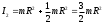 Суммарный момент инерции равен 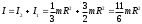 вычислим 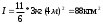 Верный ответ в) 88 кгм2. 38.2. Частица движется так, что ее радиус-вектор зависит от времени по закону 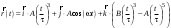 , где , где 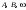 – постоянные величины, – постоянные величины, 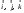 – единичные орты в декартовой системе координат. Через сколько секунд ускорение частицы окажется перпендикулярной оси z, если – единичные орты в декартовой системе координат. Через сколько секунд ускорение частицы окажется перпендикулярной оси z, если 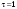 с. А = 4 м, с. А = 4 м, В = 5 м, 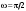 рад/с. а) 0,212 с; б) 0,312 с; в) 0,412 с; г) 0,512 с; д) 0,612 с; рад/с. а) 0,212 с; б) 0,312 с; в) 0,412 с; г) 0,512 с; д) 0,612 с;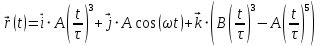 Скорость – производная от закона радиус-вектора Скорость – производная от закона радиус-вектора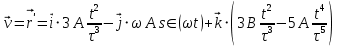 Ускорение – производная от скорости 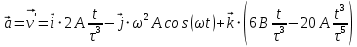 Ускорение частицы будет перпендикулярно оси Ускорение частицы будет перпендикулярно оси 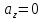 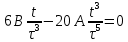 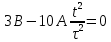 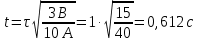 38.3. Частица начала свое движение из точки с радиусом-вектором 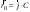 со скоростью, которая зависит от времени по закону со скоростью, которая зависит от времени по закону 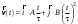 , где , где 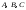 – постоянные величины, – постоянные величины, 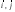 – единичные орты в декартовой системе координат. На какое расстояние от начала координат удалится частица в момент времени – единичные орты в декартовой системе координат. На какое расстояние от начала координат удалится частица в момент времени 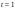 с, если с, если 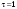 с, А = 2 м/c, В = 3 м/c, С = 4 м. с, А = 2 м/c, В = 3 м/c, С = 4 м.а) 4,10 м; б) 5,10 м; в) 6,10 м; г) 7,10 м; д) 8,10 м; 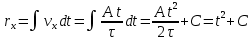 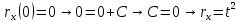 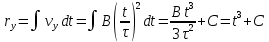 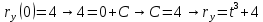 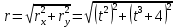 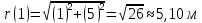 38.4. Частица из состояния покоя начала двигаться по дуге окружности радиуса 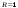 м с угловым ускорением, которое зависит от времени по закону м с угловым ускорением, которое зависит от времени по закону 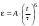 . Найти линейную скорость частицы через время . Найти линейную скорость частицы через время 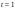 с, если с, если 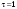 с. А = 4 с–2. с. А = 4 с–2.а) 0,171 м/с; б) 0,371 м/с; в) 0,571 м/с; г) 0,771 м/с; д) 0,971 м/с; Изменение угловой скорости за малый промежуток времени 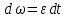 Подставим сюда зависимость углового ускорения от времени Подставим сюда зависимость углового ускорения от времени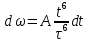 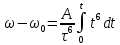 Т.к. частица начала двигаться из состояния покоя, то Т.к. частица начала двигаться из состояния покоя, то 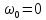 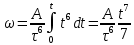 Тогда искомая линейная скорость частицы равна 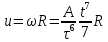 Подставим: 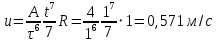 38.5. Д 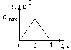 иск вращается с угловым ускорением, зависимость от времени которого задается графиком. Найти максимальную угловую скорость диска в интервале времени иск вращается с угловым ускорением, зависимость от времени которого задается графиком. Найти максимальную угловую скорость диска в интервале времени 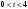 с, если с, если 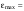 3 с–2. 3 с–2.а) 4 с–1; б) 5 с–1; в) 6 с–1; г) 7 с–1; д) 8 с–1;
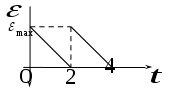 Учитывая, что математически уравнение прямой 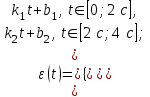 Рассмотрим моменты времени: начало движения, 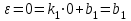 ; ;С другой стороны 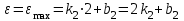 ; ;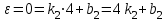 ; ;Имеем систему: 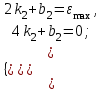 Вычтем из первого уравнения системы второе: 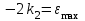 ; ;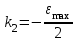 ; ;Значит: 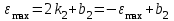 ; ;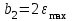 ; ;Таким образом: 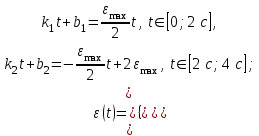 По определению углового ускорения: Имеем: Следовательно, в промежутке времени  , где , где Максимальное значение угловой скорости на первом промежутке времени: В промежутке времени 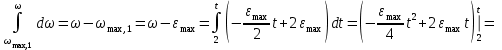 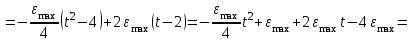 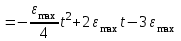 ; ;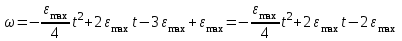 ; ;Чтобы найти максимальное значение функции 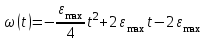 на промежутке времени на промежутке времени 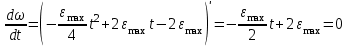 ; ;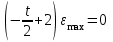 ; ;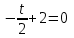 ; ;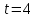 с; с;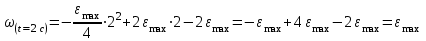 ; ;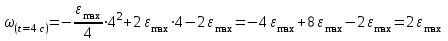 ; ;Таким образом, максимальное значение угловой скорости в промежутке времени Результат расчета: 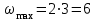 (с-1); (с-1);Ответ: в) 6 с-1 38.6. Н 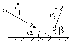 ебольшой шарик массы m летит со скоростью ебольшой шарик массы m летит со скоростью 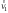 под углом = 30 к горизонтальной плоскости. После неупругого удара он отскакивает со скоростью под углом = 30 к горизонтальной плоскости. После неупругого удара он отскакивает со скоростью 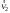 под углом =60 к плоскости. Время соударения . Найти модуль средней силы нормальной реакции опоры, действовавшей на шарик во время удара. под углом =60 к плоскости. Время соударения . Найти модуль средней силы нормальной реакции опоры, действовавшей на шарик во время удара.  8 м/с, 8 м/с,  5 м/с, = 0,01 с, m= 3 кг. 5 м/с, = 0,01 с, m= 3 кг.а) 2499 Н; б) 1499 Н; в) 499 Н; г) 299 Н; д) 199 Н; Дано:   Решение: изменение импульса в проекции на вертикальную ось  изменение импульса тела равно импульсу силы  отсюда искомая сила трения  Вычислим  38.7. Маленький шарик поместили в точку с радиусом-вектором 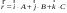 . В некоторый момент на шарик подействовали силой . В некоторый момент на шарик подействовали силой 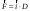 . Найти модуль момента силы относительно начала отсчета. А, В, С и D – некоторые постоянные; . Найти модуль момента силы относительно начала отсчета. А, В, С и D – некоторые постоянные; 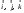 – единичные орты в декартовой системе координат. A= 4 м, В = 5 м, С = 6 м, D = 7 Н. – единичные орты в декартовой системе координат. A= 4 м, В = 5 м, С = 6 м, D = 7 Н.а) 4,7 Нм; б) 14,7 Нм; в) 34,7 Нм; г) 54,7 Нм; д) 74,7 Нм; дано A= 4 м, В = 5 м С = 6 м D = 7 Н. М-? Решение: Момент силы в данном случае равен 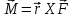 Векторное произведение двух векторов 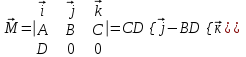 Модуль этого вектора 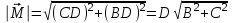 вычислим 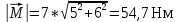 38.8. К  атушка без ниток имеющая массу m, внешний радиус R и момент инерции I,катится по горизонтальной поверхности со скоростью атушка без ниток имеющая массу m, внешний радиус R и момент инерции I,катится по горизонтальной поверхности со скоростью  без проскальзывания. Найдите кинетическую энергию этой катушки. без проскальзывания. Найдите кинетическую энергию этой катушки.m = 2 кг, R= 3 м, I= 4 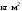 , ,  5 м/с. 5 м/с.а) 28,6 Дж; б) 30,6 Дж; в) 32,6 Дж; г) 34,6 Дж; д) 36,6 Дж; Дано: 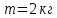 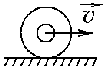 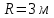 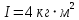 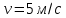 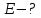 Кинетическая энергия 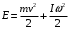 Угловая скорость 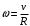 Тогда 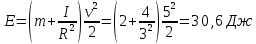 38.9. М 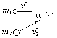 аленький пластилиновый шарик массы m1 движется горизонтально со скоростью аленький пластилиновый шарик массы m1 движется горизонтально со скоростью 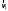 . Под углом к направлению его движения летит второй шарик массы m2 со скоростью . Под углом к направлению его движения летит второй шарик массы m2 со скоростью 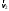 и сталкивается с первым. Шарики слипаются и движутся со скоростью и сталкивается с первым. Шарики слипаются и движутся со скоростью 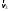 . Найдите величину скорости . Найдите величину скорости 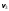 . .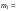 2 кг, 2 кг, 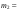 3 кг, 3 кг, 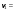 4 м/с, 4 м/с, 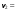 5 м/с, = 60, 5 м/с, = 60,а) 2,04 м/с; б) 3,04 м/с; в) 4,04 м/с; г) 5,04 м/с; д) 6,04 м/с; 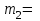 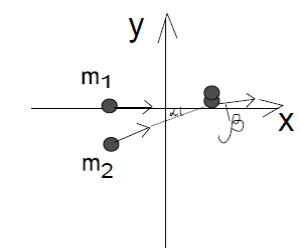 3кг, 3кг, 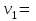 4 м/с, 4 м/с, = 60. 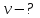 решение обозначим модуль импульса шаров после удара 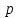 . Изобразим на рисунке ситуацию, описанную в условии . Изобразим на рисунке ситуацию, описанную в условииза законом сохранения импульса в проекции на ось ОХ 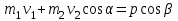 Запишем закон сохранения импульса в проекции на ось ОУ 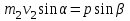 Вознесем оба последних равенства в квадрат и сложим их 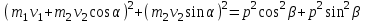 Отсюда 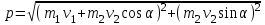 Учтем что 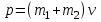 Прировняем оба последних равенства 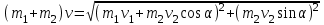 Отсюда 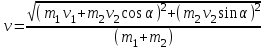 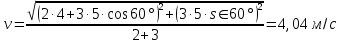 38.10. О 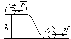 днородный шар массы m и радиуса R скатывается без проскальзывания с горки высоты h. Начальная скорость центра масс шара равна днородный шар массы m и радиуса R скатывается без проскальзывания с горки высоты h. Начальная скорость центра масс шара равна  . Найдите скорость центра масс шара после того, как он скатится с горки. Сопротивлением воздуха пренебречь. m = 3 кг, R= 4 м, . Найдите скорость центра масс шара после того, как он скатится с горки. Сопротивлением воздуха пренебречь. m = 3 кг, R= 4 м, 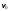 = 5 м/с, h= 6 м, g = 10 м/с2. = 5 м/с, h= 6 м, g = 10 м/с2.а) 10,5 м/с; б) 15,5 м/с; в) 20,5 м/с; г) 25,5 м/с; д) 30,5 м/с; дано m = 3 кг R= 4 м h= 6 м 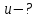 2. 2.Решение: Кинетическая энергия увеличится настолько, насколько уменьшится потенциальная энергия Начальная потенциальная энергия 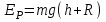 Здесь 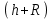 - начальная высота центра масс шара над нижней горизонталью. - начальная высота центра масс шара над нижней горизонталью. Конечная потенциальная энергии 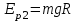 Изменение потенциальной энергии 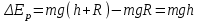 Это изменение и есть увеличение кинетической энергии 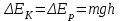 Кинетическая энергия шара состоит из энергии поступательного движения 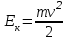 и энергии вращательного движения и энергии вращательного движения 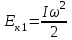 (1) (1)Подставим в (1) выражение для момента инерции шара 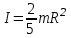 и связь его угловой скорости с линейной скоростью точек обода (это и есть скорость шара) и связь его угловой скорости с линейной скоростью точек обода (это и есть скорость шара) 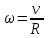 Получим 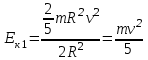 суммарная кинетическая энергия 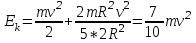 теперь запишем закон сохранения энергии 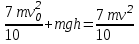 отсюда скорость шара в конце спуска 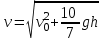 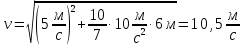 |
