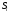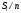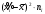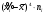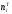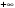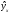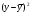Высшая математика. ТВиМС_1 вар.. Решение Найдем количество возможных исходов а Событие а студент знает все три вопроса
 Скачать 363.94 Kb. Скачать 363.94 Kb.
|
|
Вариант 1. Задание 1. 1. Студент знает 45 из 60 вопросов программы. Каждый экзаменационный билет содержит три вопроса. Найти вероятность того, что студент знает: а) все три вопроса; б) только два вопроса; в) только один вопрос экзаменационного билета. Решение: Найдем количество возможных исходов: 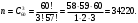 а) СобытиеА– студент знает все три вопроса. Найдем количество благоприятных исходов.  Искомая вероятность по классическому определению вероятностей равна: 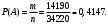 б) Событие B– студент знает только два вопроса. Найдем количество благоприятных исходов. 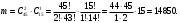 Искомая вероятность по классическому определению вероятностей равна:  в) Событие C– студент знает только один вопрос. Найдем количество благоприятных исходов.  Искомая вероятность по классическому определению вероятностей равна:  Ответ: а) 0,4147; б) 0,4340; в) 0,1381. Задание 2. 1. В городе три шоколадные фабрики. Первая выпускает 45% конфет, причем 15% из них в обертке. Вторая выпускает 35% конфет, из которых 23% в обертке. Третья выпускает 20% конфет, из них 48% в обертке. Какова вероятность, что купленная наугад конфета окажется без обертки? Решение: Событие B = {купленная наугад конфета окажется без обертки}. Гипотезы: 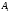 = {конфета выпущена на первой фабрике}; = {конфета выпущена на первой фабрике}; = {конфета выпущена на второй фабрике}; = {конфета выпущена на второй фабрике}; = {конфета выпущена на третьей фабрике}. = {конфета выпущена на третьей фабрике}.Из условия имеем:  Условныевероятности: 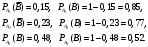 По формуле полной вероятности:  Вероятность того, что купленная наугад конфета окажется без обертки равна:  Ответ: 0,756. Задание 3. 1. Вероятность попадания в цель равна 0,25. Производится 8 выстрелов. Найти вероятность того, что будет: а) не менее семи попаданий; б) не менее одного попадания. Решение: По условию имеем  Воспользуемся формулой Бернулли: 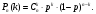 а) Событие A – при  выстрелах будет не менее 7 попаданий, можно рассматривать как сумму несовместных событий: 7 попаданий из 8 и все 8 попаданий. выстрелах будет не менее 7 попаданий, можно рассматривать как сумму несовместных событий: 7 попаданий из 8 и все 8 попаданий. б) Событие B – при  выстрелах будет не менее 1 попадания. Вычислим с использованием противоположного события. выстрелах будет не менее 1 попадания. Вычислим с использованием противоположного события. Ответ: а) 0,00038; б) 0,89989. Задание 4. Случайная величина Х задана функцией распределения F(х). Найдите плотность распределения вероятностей f(x), математическое ожидание и дисперсию случайной величины. Постройте графики функций F(х) и f(x). 1.  Решение: Найдем функцию плотности распределения:  Вычислим математическое ожидание: 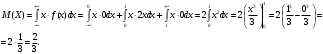 Дисперсию вычислим по формуле:  В данном случае:  Таким образом:  Построим графики функций F(х) и f(x).   Ответ:  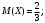  Задание 5. Известны математическое ожидание а и среднее квадратическое отклонение  нормально распределенной случайной величины. Найдите вероятность попадания этой величины в заданный интервал нормально распределенной случайной величины. Найдите вероятность попадания этой величины в заданный интервал 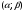 . .1.  Решение: Вероятность попадания случайной величины в интервал (2; 13) вычислим по формуле:  где  – функция Лапласа, которая находится по таблице значения функции Лапласа. – функция Лапласа, которая находится по таблице значения функции Лапласа. Искомая вероятность равна:  Ответ: 0,7506. Задание 6. Математические ожидания и дисперсии статистически независимых величин X и Y равны  и и  . Вычислите математическое ожидание и дисперсию функции Z = 2XY – 9. . Вычислите математическое ожидание и дисперсию функции Z = 2XY – 9.1.  Решение: Используя свойства математического ожидания и дисперсии вычислим: – математическое ожидание функции Z = 2XY – 9:  – дисперсию функции Z = 2XY – 9: 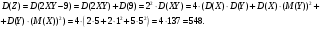 Ответ: 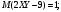  Задание 7. Дисперсия случайной величины X равна σ2. Оцените вероятность того, что случайная величина отклонится от своего математического ожидания не более чем на величину ε. 1. 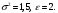 Решение: Воспользуемся неравенством Чебышева:  Вероятность того, что случайная величина отклонится от своего математического ожидания не более чем на 2 равна:  Ответ:  Задание 8. По данной выборке случайной величины: а) постройте гистограмму и график эмпирической функции распределения; б) вычислите все основные эмпирические характеристики: выборочное среднее, выборочную дисперсию и выборочное среднее квадратичное отклонение, коэффициент вариации, размах выборки, асимметрию и эксцесс. в) проверьте по критерию 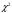 -Пирсона гипотезу о нормальности распределения выборки с доверительной вероятностью 0,95. -Пирсона гипотезу о нормальности распределения выборки с доверительной вероятностью 0,95.1.
Решение: Проранжируем данную выборку, расположив варианты в порядке возрастания:
Построим интервальный ряд. Количество интервалов определим по формуле Стерджесса  Количество интервалов  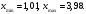 Длина интервала:  За начало 1го интервала возьмем 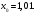 Подсчитаем, сколько значений попало в каждый из полученных интервалов. Подсчитаем, сколько значений попало в каждый из полученных интервалов.Вычислим накопленные частоты и относительные накопленные частоты по формуле  Получим интервальный ряд Получим интервальный рядТаблица 1
а) Строим гистограмму, используя исходные данные.  Построим эмпирическую функцию распределения  по рассчитанным данным, указанным в таблице. по рассчитанным данным, указанным в таблице.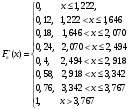 График этой функции изобразим на рисунке.  б) Для удобства вычислений характеристик расчеты сумм, входящих в формулы проведем с помощью табл. следующего вида: Таблица 2
Выборочное среднее равно:  Выборочная дисперсия: 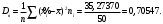 Выборочное среднее квадратичное отклонение:  Коэффициент вариации:  Размах выборки: 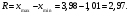 Асимметрия:  Эксцесс: 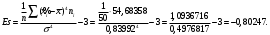 в) Примем в качестве нулевой гипотезу  : выборка, имеет нормальное распределение с параметрами : выборка, имеет нормальное распределение с параметрами  Проверим ее, пользуясь критерием Пирсона при уровне значимости Проверим ее, пользуясь критерием Пирсона при уровне значимости  Для каждого интервала, используя данные таблицы 1, находим теоретические частоты по формуле: 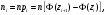 где Φ(z) – табличные значения функции Лапласа, где Φ(z) – табличные значения функции Лапласа,  Данные расчеты представим в таблице 3. При использовании приведенной формулы теоретических частот наименьшее значение аргумента функции Лапласа 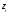 для первого интервала выборки принято равным для первого интервала выборки принято равным  а наибольшее значение аргумента а наибольшее значение аргумента  для последнего интервала для последнего интервала  Таблица 3
Проверка:  Проверяем согласие гипотезы о нормальном законе распределения изучаемой выборки по критерию Пирсона.  Число степеней свободы k = s – 1 – r = 7 – 1 – 2 = 4, где s − число интервалов, а k – число параметров нормального распределения. По таблице критических точек распределения χ2 для уровня значимости α = 0,05 находим:  . .Так как 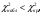 следовательно, гипотеза о нормальном законе распределения выборки принимается. следовательно, гипотеза о нормальном законе распределения выборки принимается.Задание 9. Считая, что две первые строки таблицы задания 8 и следующие три строки являются двумя независимыми выборками из нормального распределения, проверьте при уровне значимости 0,05 гипотезы о равенстве математических ожиданий (критерий Стьюдента) и о равенстве дисперсий (критерий Фишера). Решение:
Проверим гипотезу 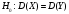 при конкурирующей гипотезе при конкурирующей гипотезе  при уровне значимости при уровне значимости  Сначала вычислим средние значения и исправленные дисперсии выборок X и Y. Средние значения: 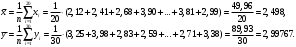 Исправленные дисперсии:  Вычислим наблюдаемое значение критерия, как отношение большей исправленной дисперсии к меньшей: 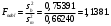 По условию, конкурирующая гипотеза имеет вид 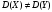 , поэтому критическая область – двусторонняя. , поэтому критическая область – двусторонняя. По таблице критических точек распределения F Фишера при уровне значимости  и числам степеней свободы и числам степеней свободы  и и  (так как 0,75391 > 0,66240) находим критическую точку: (так как 0,75391 > 0,66240) находим критическую точку: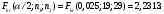 Так как 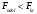 – нулевую гипотезу принимаем. Таким образом дисперсии выборок X и Y равны при уровне значимости – нулевую гипотезу принимаем. Таким образом дисперсии выборок X и Y равны при уровне значимости  Проверим гипотезу  при конкурирующей гипотезе при конкурирующей гипотезе 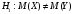 при уровне значимости при уровне значимости  Вычислим наблюдаемое значение критерия, как отношение большей исправленной дисперсии к меньшей: 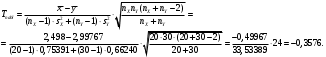 По условию, конкурирующая гипотеза имеет вид  , поэтому критическая область – двусторонняя. , поэтому критическая область – двусторонняя. По таблице критических точек распределения Стьюдента при уровне значимости  и числу степеней свободы и числу степеней свободы 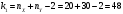 находим критическую точку: находим критическую точку: Так как  – нулевую гипотезу принимаем. Таким образом математические ожидания выборок X и Y равны при уровне значимости – нулевую гипотезу принимаем. Таким образом математические ожидания выборок X и Y равны при уровне значимости  Задание 10. При изучении зависимости между величиной Y и величиной X было получено 15 пар соответствующих значений этих величин. Аппроксимируйте статистическую зависимость величины Y от X линейной функцией y = ax + b. Вычислите остаточную дисперсию и коэффициент детерминации. 1.
Решение: Для расчета параметров  и и 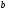 линейной регрессии линейной регрессии 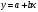 решаем систему нормальных уравнений относительно решаем систему нормальных уравнений относительно  и и 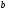 : : По исходным данным рассчитываем 
Подставим вычисленные суммы в систему для определения параметров линейной регрессии:  Уравнение регрессии имеет вид:  . .Вычислим остатки. Для этого вычислим 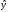 , подставив значения x в уравнение регрессии , подставив значения x в уравнение регрессии  . Затем вычислим квадрат разности . Затем вычислим квадрат разности  . .Остаточную дисперсию вычислим по формуле:  Коэффициент детерминации равен:  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||