Практические задания. Решение Найдем уравнение изоклин. По определению уравнение имеет вид f(x,y)k, где kconst. Следовательно 2(1)
 Скачать 100.35 Kb.
|
|
1. Методом изоклин построить интегральные кривые уравнения 𝑑𝑦  =2𝑥(1−𝑦) 𝑑𝑥 Решение Найдем уравнение изоклин. По определению уравнение имеет вид f(x,y)=k, где k=const. Следовательно 𝑘=2𝑥(1−𝑦) 𝑘 1−𝑦=  2𝑥 𝑘 𝑦=1− 2𝑥 Изоклины представляют собой семейство гипербол. При k=0 имеем y=1 и tgα=k⇔tgα=0⇔α=0° 1 При k=1 имеем 𝑦=1−  и tgα=1⇔α=45° 2𝑥 При k=-1 имеем 𝑦=1+ 1 и tgα=-1⇔α=135° 2𝑥 1 При k=2 имеем 𝑦=1− и tgα=1⇔α≈63° 𝑥 При k=-2 имеем 𝑦=1+ 1 и tgα=-1⇔α≈117° 𝑥 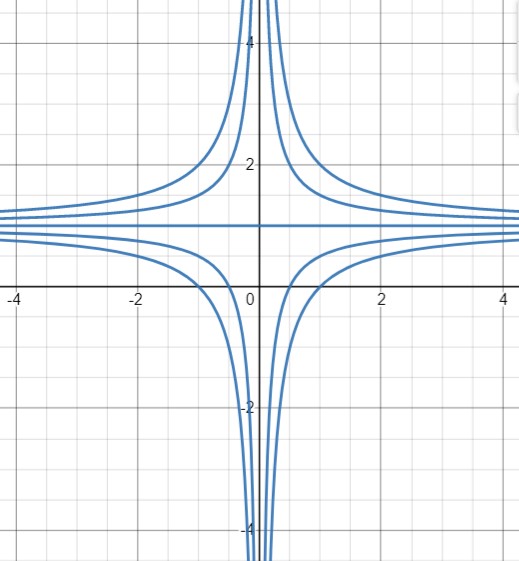 2. Решить уравнение, допускающее понижения порядка 𝑥2𝑦′′ =𝑦′2 Решение: Пусть 𝑦′ =𝑧(𝑥), получим дифференциальное уравнение первого порядка 𝑥2𝑧′ =𝑧2 Разделяя переменные и интегрируя, имеем 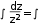 𝑑𝑥 𝑥      𝑧 𝑧 𝑥 𝑥 𝑧  𝑦′ 𝑥 𝑦   𝑑𝑥+𝐶2 =  𝑥, если С   𝐶 𝐶  𝑥2  +𝐶2, если С 2 { С2, если С  3. Решить систему уравнений 𝑑𝑥 𝑡 = 𝑑𝑡 𝑦  {𝑑𝑦 𝑡 =− 𝑑𝑡 𝑥 Решение: 𝑡𝑑𝑡=𝑦𝑑𝑥 { 𝑡𝑑𝑡=−𝑥𝑑𝑦 Так как левые части одинаковые в двух уравнениях системы, то приравняем их правые части 𝑦𝑑𝑥=−𝑥𝑑𝑦 Решим уравнение с разделяющимися переменными 𝑑𝑦 𝑑𝑥 =− 𝑦 𝑥 𝑑𝑦 𝑑𝑥 ∫ =−∫ 𝑦 𝑥ln|𝑦|=−ln|𝑥|+𝐶 𝐶 𝑦=  𝑥 4. Вероятность появления события в каждом испытании равна 0,7. Сколько нужно провести испытаний, чтобы наивероятнейшее число появлений события равнялось 10? Решение: По условию 𝑘0 =10,𝑝=0,7,𝑞=1−𝑝=0,3. Воспользуемся двойным неравенством, из которого определяется наивероятнейшее число 𝑘0: 𝑛𝑝−𝑞≤𝑘0 ≤𝑛𝑝+𝑝 Подставляя данные задачи, получим неравенство 0,7n−0,3≤10≤0,7n+0,7 Решаем отдельно каждое неравенство, входящее в данное двойное неравенство:
Окончательно имеем: 13,29 ≤ n ≤ 14,71, т.е. n может быть равно 14. |