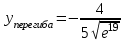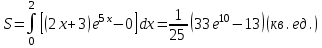Итоговое задание математика. Итоговое задание. Решение. Найти область определения, точки разрыва или Точек разрыва нет
 Скачать 125.25 Kb. Скачать 125.25 Kb.
|
|
Задание. Для функции 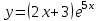 : : 1. Найти область определения, точки разрыва. 2. Исследовать функцию на четность, периодичность. 3. Исследовать поведение функции на концах области определения. Указать асимптоты. 4. Найти промежутки монотонности. Точки экстремума. 5. Найти промежутки выпуклости. Точки перегиба. 6. Найти площадь фигуры, ограниченной графиком функции 𝑦 = (2𝑥 + 3)𝑒 5𝑥 и прямыми 𝑥 = 0, 𝑥 = 2, 𝑦 = 0. Результаты исследования оформить в виде таблицы. Решение. 1. Найти область определения, точки разрыва. 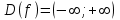 или или 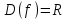 Точек разрыва нет. 2. Исследовать функцию на четность, периодичность. 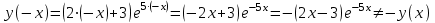 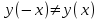 Отсюда следует, что функция не является нечетной и не является четной. Функция не периодическая. 3. Исследовать поведение функции на концах области определения. Указать асимптоты. 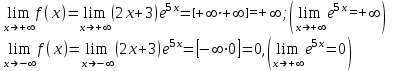 При х→-∞ функция стремится к нулю, При х→+∞ функция стремится +∞. Находим наклонную асимптоту 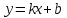 : :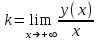 = =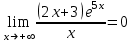 . .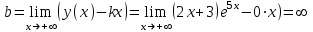 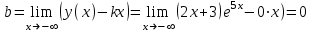 Наклонных асимптот нет. Следовательно, у = 0 горизонтальная асимптота при Так как функция не имеет точек разрыва, то это означает, что вертикальных асимптот нет. 4. Найти промежутки монотонности. Точки экстремума. 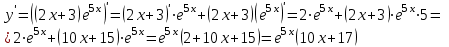 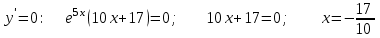
В окрестности точки 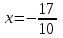 производная функции меняет знак с (-) на (+). Следовательно, точка производная функции меняет знак с (-) на (+). Следовательно, точка 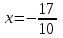 - точка минимума. - точка минимума.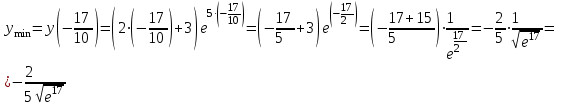 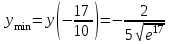 5. Найти промежутки выпуклости. Точки перегиба. 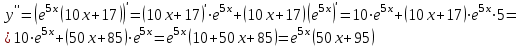 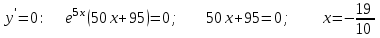
В окрестности точки 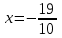 производная функции меняет знак с (-) на (+). Следовательно, точка производная функции меняет знак с (-) на (+). Следовательно, точка 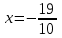 - точка перегиба. - точка перегиба.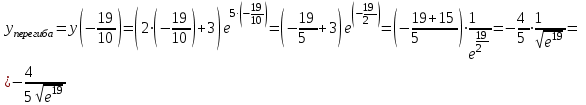 6. Найти площадь фигуры, ограниченной графиком функции 𝑦 = (2𝑥 + 3)𝑒 5𝑥 и прямыми 𝑥 = 0, 𝑥 = 2, 𝑦 = 0. 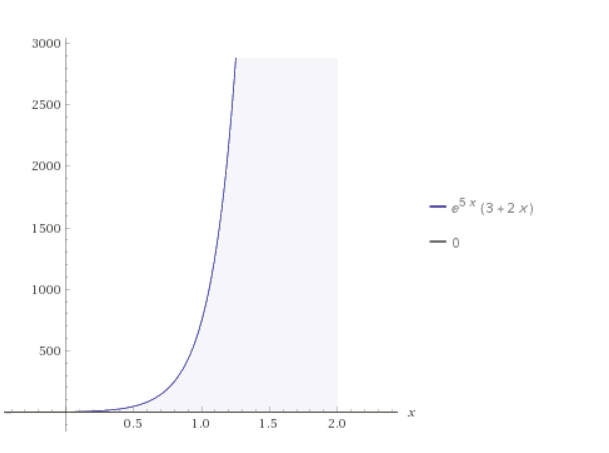 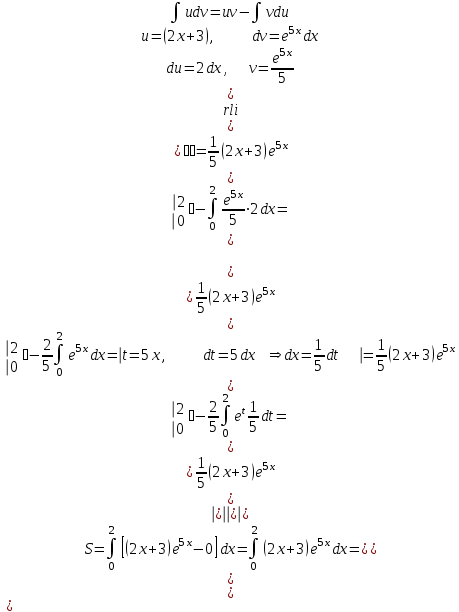 По результатам исследований построим график. 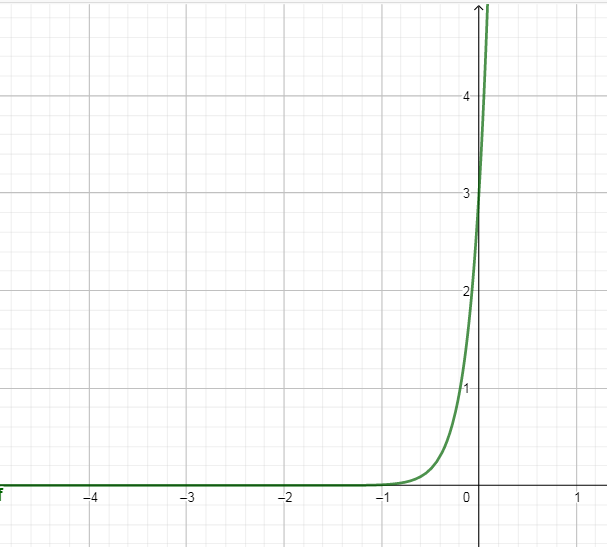 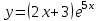
|

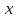
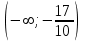
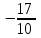
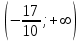
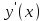
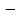
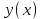
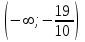
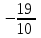
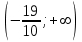
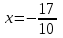 ,
,