Функция издержек имеет вид ????(????) = ???? 0,1 ∙ ????2. Решение Определим функцию валовой выручки от продажи х ед продукции R(x) p 0 x 50x Найдем функцию прибыли
 Скачать 42.22 Kb. Скачать 42.22 Kb.
|
|
Контрольная работа Вариант __45_________________________________________________ Функция издержек имеет вид 𝐶(𝑥) = 𝑥 + 0,1 ∙ 𝑥2. Доход от реализации единицы продукции равен 50. Найти максимальное значение прибыли, которое может получить производитель. Решение: Определим функцию валовой выручки от продажи х ед. продукции: R(x) = P0 ∙ x = 50x Найдем функцию прибыли: 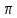 (x) = R(x) – C(x) = 50x – (x + 0,1x2) = 49x – 0,1x2 (x) = R(x) – C(x) = 50x – (x + 0,1x2) = 49x – 0,1x2Исследуем её на экстремум, найдем первую и вторую производные: 𝜕 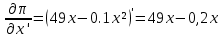 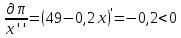 (вогнутость) (вогнутость)Точка глобального экстремума х = 245, вогнутость показывает на то что эта точка – глобальный максимум. Следовательно, максимизирующий прибыль объем производства равен 21 ед. Максимальная прибыль составит: 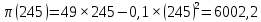 Ответ: 6002,2 Имеются данные (таблица) о работе системы нескольких отраслей в прошлом периоде и план выпуска конечной продукции 𝑌1 в будущем периоде, усл. ден. ед.
Найти матрицы прямых и полных затрат, а также выпуск валовой продукции в плановом периоде, обеспечивающей выпуск конечной продукции 𝑌1. Решение: Найдем валовый выпуск отраслей: 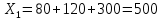 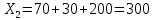 Найдем матрицу прямых затрат. Ее элементы можно найти по формуле: 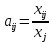 Подставляя числовые значения, получаем матрицу прямых затрат: А = 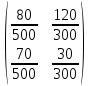 = = 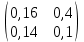 Преобразуем формулу (модель Леонтьева) X = AX + Y X - AX = Y (E - A)X = Y (E - A)(E - A)-X X = (E - A)-Y Матрица полных затрат B = (E-A)- E-A = 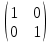 - - 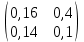 = = 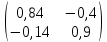 Вычислим определитель матрицы (E-A): 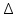 = 0,84×0,9-(-0,4 × (-0,14)) = 0,7 = 0,84×0,9-(-0,4 × (-0,14)) = 0,7Алгебраические дополнения: A11 = 0,9 A12 = 0,14 A21 = 0,4 A22 = 0,84 Определим матрицу полных затрат, находя обратную матрицу E-A: B = 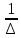 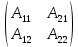 = = 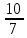 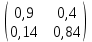 = = 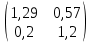 Найдем выпуск валовой продукции в плановом периоде по формуле: Xn = B × 𝑌1 Xn = 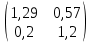 ×( ×( 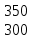 ) = ( ) = (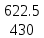 ) )Ответ: а) матрица прямых затрат: 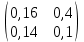 ; ; б) матрица полных затрат: 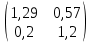 ; ; в) выпуск валовой продукции: ( 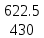 ). ).Потребитель имеет возможность потратить сумму 1000 (ден. ед.) на приобретение x единиц первого товара и y единиц второго товара. Задана функция полезности 𝑈(𝑥, 𝑦) и цены 𝑝1, 𝑝2 единицы соответственно первого и второго товаров. Найти значения (𝑥, 𝑦) , при которых полезность для потребителя будет наибольшей: 𝑈(𝑥, 𝑦) = 0,5 ∙ ln(𝑥 − 2) + 2 ∙ ln(𝑦 − 1); 𝑝1 = 0,2, 𝑝2 = 4 Линии уравнения функции полезности (С - константа): Пусть 𝑈(𝑥, 𝑦) = С, тогда и 0,5 ∙ ln(𝑥 − 2) + 2 ∙ ln(𝑦 − 1) = С Воспользуемся свойствами логарифмов: ln (𝑥 − 2)0,5 ∙ (y − 1)2 = C отсюда: (y – 1)2 = 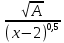 где А = ес где А = есТаким образом линии уравнения представляют собой график функции кривой безразличия: y = 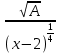 + 1 + 1Максимальное значение А, а, следовательно, С достигается в том случае, если соответствующая кривая безразличия касается прямой (линии уровня затрат) 0,2х + 4y = 1000. Т.к. градиент в каждой точке перпендикулярен линии уровня, то из этого следует, что условие максимальности прибыли может быть сформировано так: Grad U(x,y) ⊥ (0,2x + 4y = 1000) Так как y = 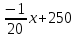 , то k1 = , то k1 = 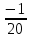 , ,условный коэффициент прямой, проходящий через Grad U равен: k2 = 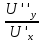 = = 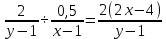 из условия перпендикулярности прямых имеем: k1 = - 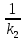 , т. е. , т. е. 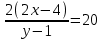 , отсюда: , отсюда: 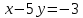 k2 = 20 k1 = 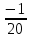 Найдем оптимальное распределение потребления товаров: 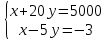 , отсюда , отсюда 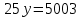 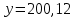 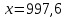 Ответ: 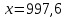 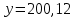 Известно, что рост числа 𝑦 = 𝑦(𝑡) жителей некоторого района описывается уравнением 𝑑𝑦 𝑑𝑡 = 0,2 ∙ 𝑦 𝑚 ∙ (𝑚 − 𝑦), где m – максимально возможное число жителей для данного района. В начальный момент времени число жителей составляло 1 % от максимального. Через какой промежуток времени оно составит 80 % от максимального? Решение: Разделяя переменные в уравнении, приходим к следующему равенству: 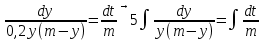 Выполняя почленное интегрирование этого равенства, получаем: 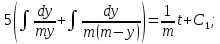 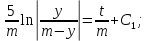 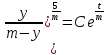 , где , где 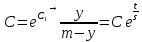 Из начальных условий находим значение постоянной С. Так как 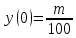 , то , то 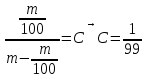 . А значит, . А значит, 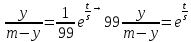 Выразим функцию t из данного равенства: 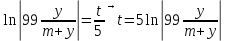 Принимая во внимание, что 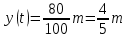 , получим: , получим: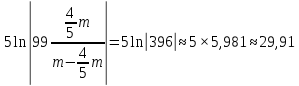 Ответ:29,91 Распределение вероятностей случайной величины Х задается интегральной функцией распределения: F(x) = 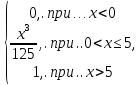 Построить график функции плотности распределения вероятностей случайной величины Х. Вычислить вероятность попадания случайной величины в интервал (2;3). Найти для случайной величины Х математическое ожидание и среднее квадратическое отклонение. Решение: График функции имеет вид: 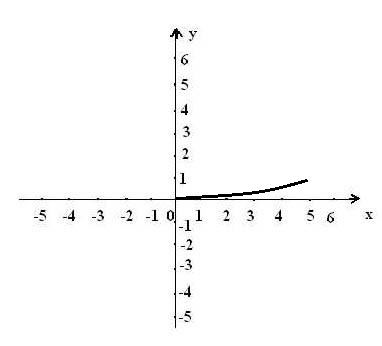 Вероятность попадания случайной величины в интервал (2;3) равна: P(2 < x < 3) = F(3) - F(2) 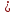 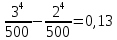 Математическое ожидание равно: 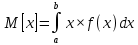 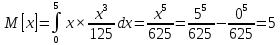 Для нахождения среднего квадратичного отклонения определим дисперсию: 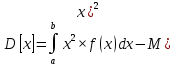 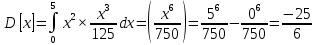 Среднее квадратическое отклонение равно: 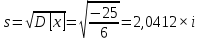 Ответ: Вероятность попадания случайной величины в интервал (2;3) = 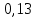 ; ;математическое ожидание = 5; квадратическое отклонение = 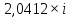 |
