Задачи по теплоемкости. Задачи по теплоемкости 2. Решение Определим истинную молярную теплоемкость газов при постоянном давлении по формуле
 Скачать 40.4 Kb. Скачать 40.4 Kb.
|
|
Задание 1. По зависимости истинной молярной изобарной теплоемкости газа в идеально-газовом состоянии от абсолютной температуры построить в масштабе график 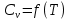 в интервале температур в интервале температур 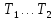 и определить с его помощью количество подведенной к газу удельной теплоты. Ту же удельную теплоту рассчитать через среднюю массовую изохорную теплоемкость газа, а также через постоянное значение изохорной массовой теплоемкости газа, полученной на основании молекулярно-кинетической теории. Для заданных абсолютных температур определить истинные молярную, массовую и объемную изобарные и изохорные теплоемкости газа. и определить с его помощью количество подведенной к газу удельной теплоты. Ту же удельную теплоту рассчитать через среднюю массовую изохорную теплоемкость газа, а также через постоянное значение изохорной массовой теплоемкости газа, полученной на основании молекулярно-кинетической теории. Для заданных абсолютных температур определить истинные молярную, массовую и объемную изобарные и изохорные теплоемкости газа. Дано: Пентан 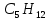 ; ;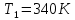 ; ;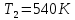 . .Решение: Определим истинную молярную теплоемкость газов при постоянном давлении по формуле 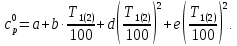 Коэффициенты для пентана по приложению П.1.3: 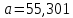 , , 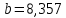 , , 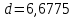 , , 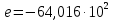 1) при температуре 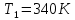 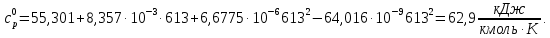 2) при температуре 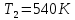 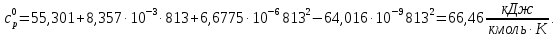 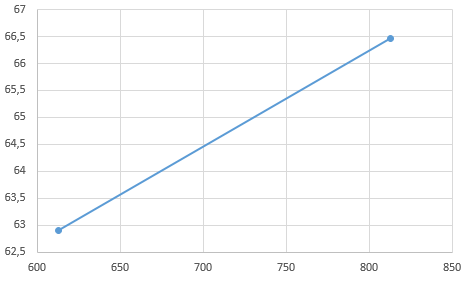 Средняя температура равна 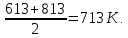 Средняя теплоемкость равна 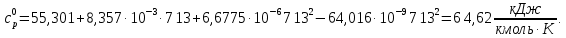 Среднюю массовую теплоемкость находим по формуле: 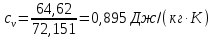 Количество подведенной теплоты 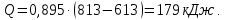 Объемную теплоемкость находим по формуле:  Задание 2. Газовая смесь массой 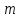 , заданная молярными долями (в процентах), нагревается при постоянном абсолютном давлении , заданная молярными долями (в процентах), нагревается при постоянном абсолютном давлении 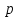 в рекуперативном теплообменном аппарате от температуры в рекуперативном теплообменном аппарате от температуры 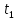 до температуры до температуры 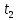 . Определить: . Определить:1) массовый состав смеси; 2) среднюю молекулярную массу; 3) газовую постоянную смеси; 4) парциальные давления компонентов через объемные и массовые доли; 5) парциальные объемы и плотность смеси при нормальных и рабочих условиях 6) средние массовые изобарные теплоемкости компонентов и смеси в интервале температур 7) количество отведенной теплоты. Дано: 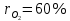 ; ;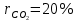 ; ;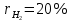 ; ;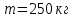 ; ;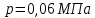 ; ;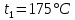 ; ;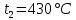 . .Решение: Т.к. смесь задана объемными долями, то определяем молярные массы компонентов 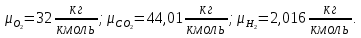 определяем молярную массу смеси по формуле 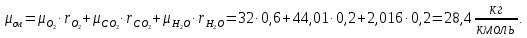 Определим парциальные давления компонентов: 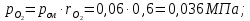 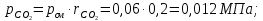 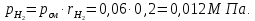 Перевод объёмных долей в массовые 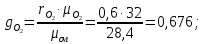 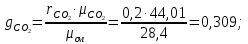 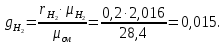 Газовые постоянные компонентов смеси: 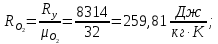 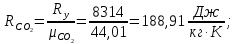 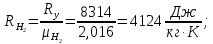 Газовая постоянная смеси, через массовые доли компонентов: R = Σ(giRi) = 0,676·259,81 + 0,309·188,91 + 0,015·4124 = 295,86 Дж/(кг·К). Парциальные давления компонентов смеси через массовые доли: 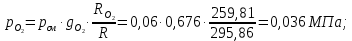 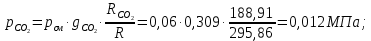 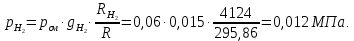 Определение средних теплоемкостей смеси: а) мольные для температур t2 = 430ºC и t1 = 175ºC из П.4: (сpm)0430 = Σ(сpm)i0430ri = 30,5478 0,6 + 42,209 0,2 + 29,389 0,2 = 32,648 кДж/(кмольК); (сpm)0175 = Σ(сpm)i0175ri = 29,8373 0,6 + 39,578 0,2 + 29,043 0,2 = 31,626 кДж/(кмольК); (сpm) 175430 = [(сpm)0430 t2 – (сpm)0175 t1]/(t2 – t1) = = (32,648·430 – 31,626·175)/(430 –175) = 33,349 кДж/(кмоль·К); (сvm) 175430 = (сpm) 175430 – 8,314 = 33,349 – 8,314 = 25,035 кДж/(кмольК); б) массовые: сpm175430 = (сpm) 175430 / μ = 33,349/28,4 = 1,174 кДж/(кгК); сvm175430 = (сvm) 175430 / μ = 25,035/28,4 = 0,8815 кДж/(кгК). 8. Определение теплоты на нагревание от t1 до t2: 250 кг смеси при p = сonst и 𝜐 = сonst: Q1 = mcpm 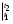 (t2 – t1) = 250 1,174 (430 – 175) = 74842,5 кДж; (t2 – t1) = 250 1,174 (430 – 175) = 74842,5 кДж;Q2 = mcvm 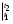 (t2 – t1) = 250 0,8815 (430 – 175) = 56195,6 кДж. (t2 – t1) = 250 0,8815 (430 – 175) = 56195,6 кДж.Задание 3. Природный газ в количестве 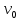 охлаждается при постоянном давлении охлаждается при постоянном давлении 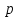 в аппарате воздушного охлаждения (АВО) от температуры в аппарате воздушного охлаждения (АВО) от температуры 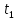 до температуры до температуры 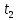 . Определить массовый состав и характеристики природного газа, изменение истинной молярной изобарной теплоемкости природного газа при охлаждении, количество отводимой от газа теплоты и расход атмосферного воздуха на охлаждение, если температура воздуха в АВО увеличивается от . Определить массовый состав и характеристики природного газа, изменение истинной молярной изобарной теплоемкости природного газа при охлаждении, количество отводимой от газа теплоты и расход атмосферного воздуха на охлаждение, если температура воздуха в АВО увеличивается от 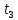 до до 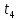 . .Дано: Месторождение – Оренбургское; 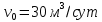 ; ;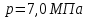 ; ;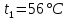 ; ;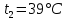 ; ;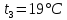 ; ;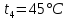 . .Решение: Химический состав газа Оренбургского месторождения: 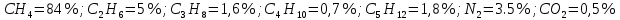 Молекулярные массы составляющих смесь газов равны (по данным физических характеристик компонентов газа из справочных таблиц): 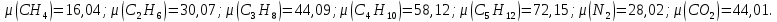 Молекулярная масса природного газа определяется по уравнению 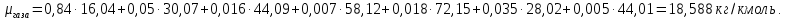 Массовые концентрации отдельных компонентов смеси равны: 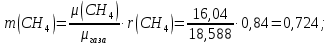 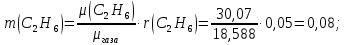 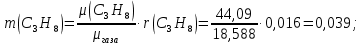 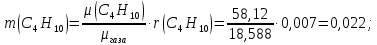 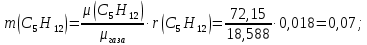 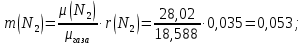 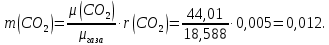 Так что массовый состав газа в процентах равен: 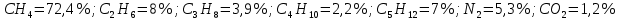 Определяем объемную теплоемкость смеси по формуле 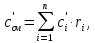 Введем следующие обозначения: 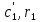 – объемная теплоемкость и объемная доля метана (СН4); – объемная теплоемкость и объемная доля метана (СН4);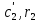 - объемная теплоемкость и объемная доля этана (С2Н6); - объемная теплоемкость и объемная доля этана (С2Н6);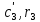 - объемная теплоемкость и объемная доля пропана (С3Н8); - объемная теплоемкость и объемная доля пропана (С3Н8);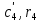 - объемная теплоемкость и объемная доля бутана (С4Н10); - объемная теплоемкость и объемная доля бутана (С4Н10);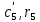 - объемная теплоемкость и объемная доля пентана (С5Н12); - объемная теплоемкость и объемная доля пентана (С5Н12);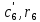 - объемная теплоемкость и объемная доля углекислого газа (СО2); - объемная теплоемкость и объемная доля углекислого газа (СО2);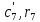 - объемная теплоемкость и объемная доля азота (N2). - объемная теплоемкость и объемная доля азота (N2).Объемные теплоемкости компонентов определим в зависимости от атомности газов. Значения 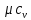 для этого берем из табл.П1-2. для этого берем из табл.П1-2.Метан, этан, пропан, бутан, пентан и углекислый газ – трех- и многоатомные газы, поэтому 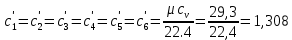 кДж/(м3·К). кДж/(м3·К).Азот – двухатомный газ, для него объемная теплоемкость 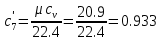 кДж/(м3·К). кДж/(м3·К).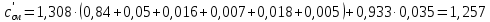 кДж/(м3·К). кДж/(м3·К).Рассчитываем количество подведенного тепла по формуле 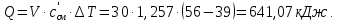 Расход воздуха на охлаждение 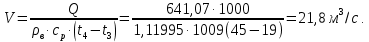 |
