Основы теории цепей. Решение Определяем токи в ветвях

• Название: Решение Определяем токи в ветвях
• Анкор: Основы теории цепей
• Дата: 24.02.2022
• Размер: 393 Kb.
• Имя файла: 5.doc
• Тип: Решение; #371978

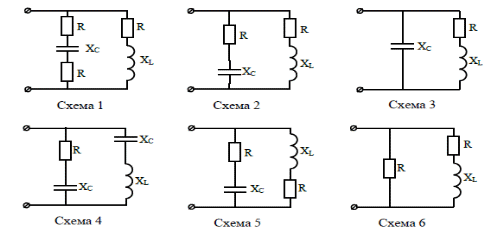
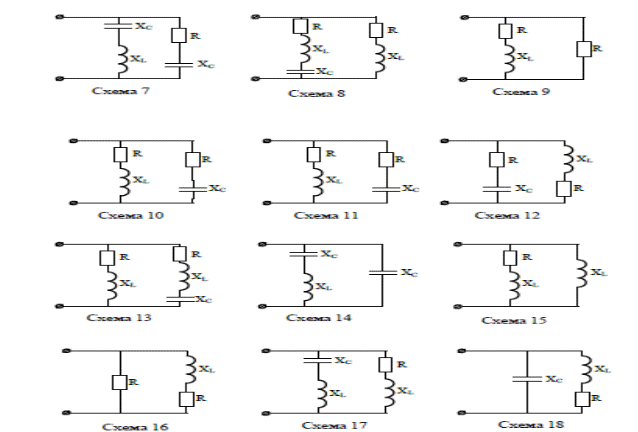
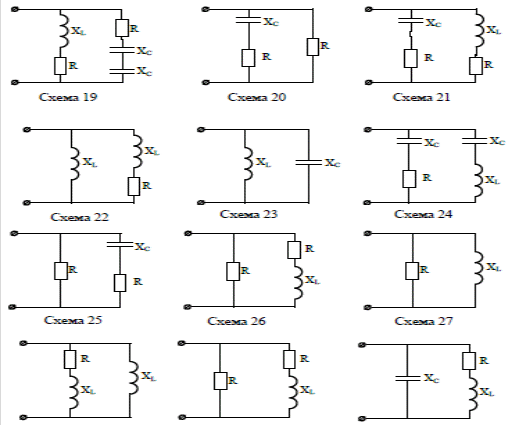
Пример 1 Катушка с активным сопротивлением R = 20 Ом и индуктивным X_L = 15 Ом соединена параллельно с конденсатором, емкостное сопротивление которого X_C = 50 Ом.

Определить токи в ветвях и в неразветвленной части цепи; активные и реактивные мощности ветвей и всей цепи; полную мощность цепи; углы сдвига фаз между током и напряжением в каждой ветви и во всей цепи; начертить в масштабе векторную диаграмму.

К 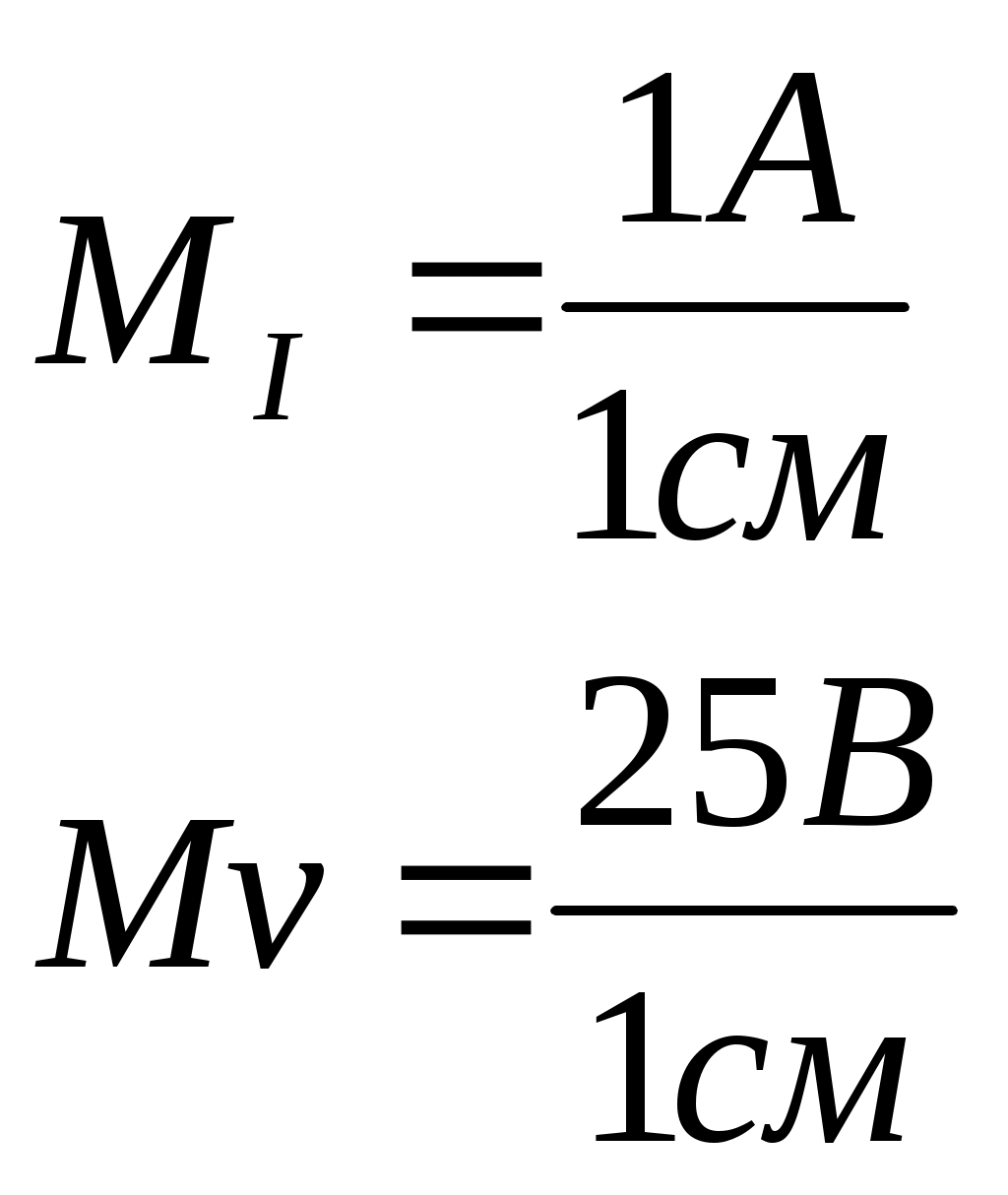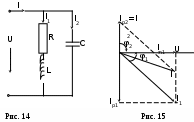цепи приложено напряжение U = 100 В.

Решение:

1. 
   Определяем токи в ветвях: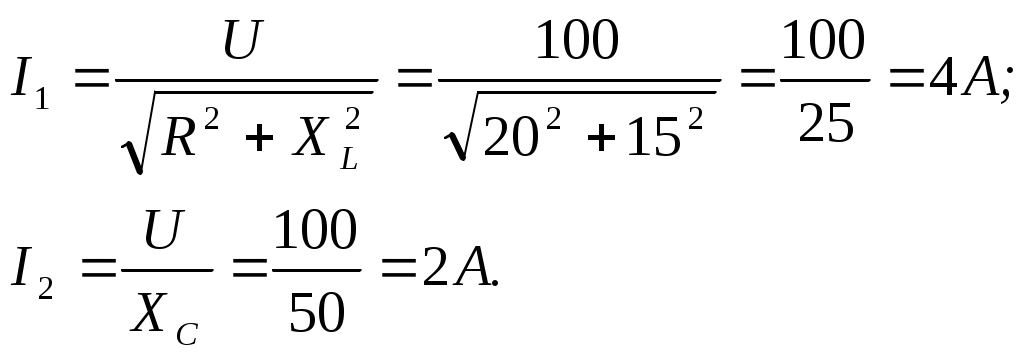
   

2. 
   Углы сдвига фаз в ветвях будем находить по синусам во избежание потери знаков углов: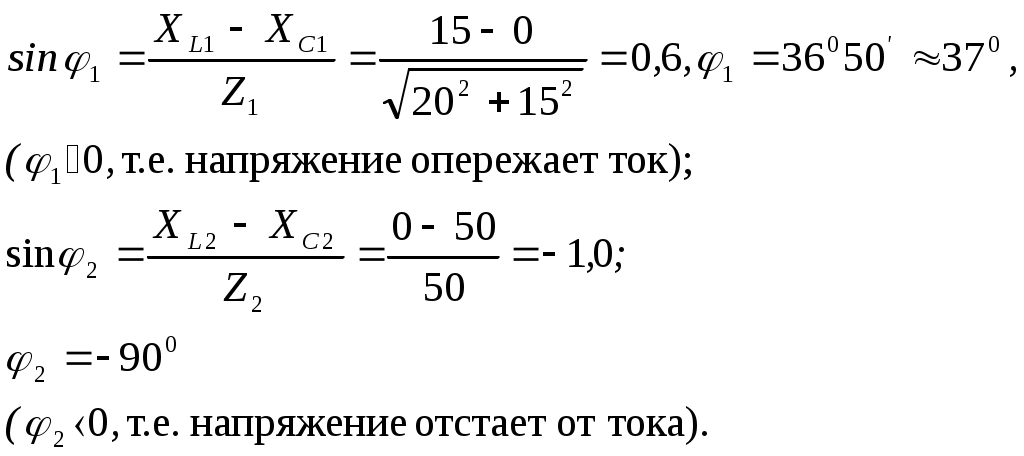
   

По таблице Брадиса находим: cos ₁ = cos 36⁰50’=0,8.

3. 
   Активные и реактивные составляющие токов ветвей: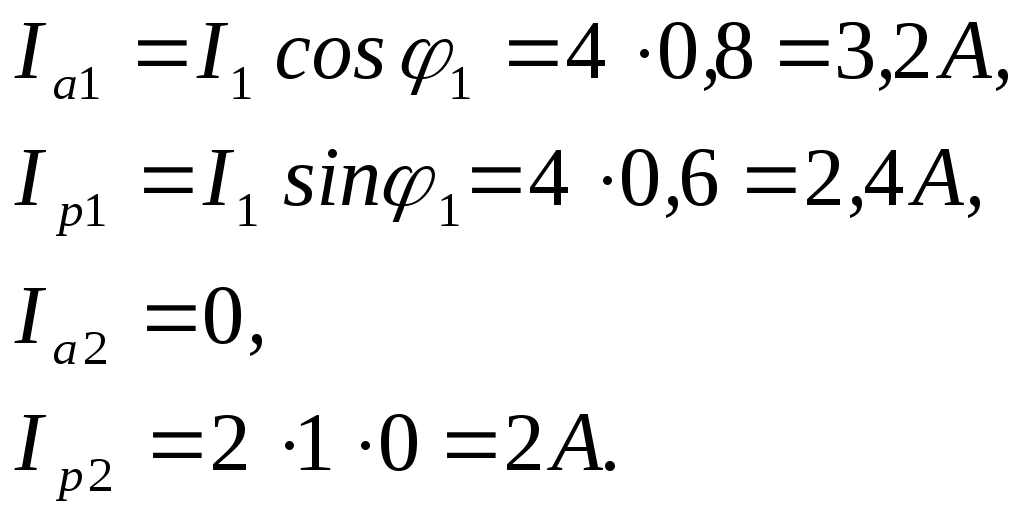
   
4. 
   Ток в неразветвленной части цепи:
   

5. 
   Активные мощности ветвей и всей цепи: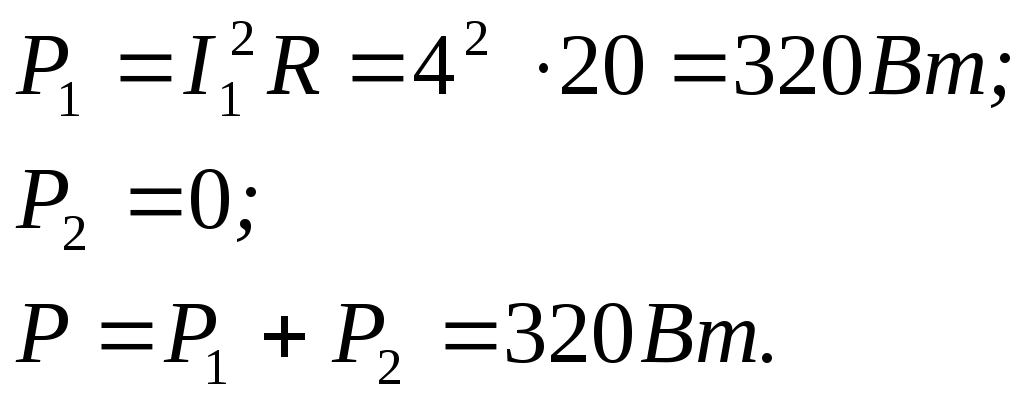
   
6. 
   Реактивные мощности ветвей и всей цепи: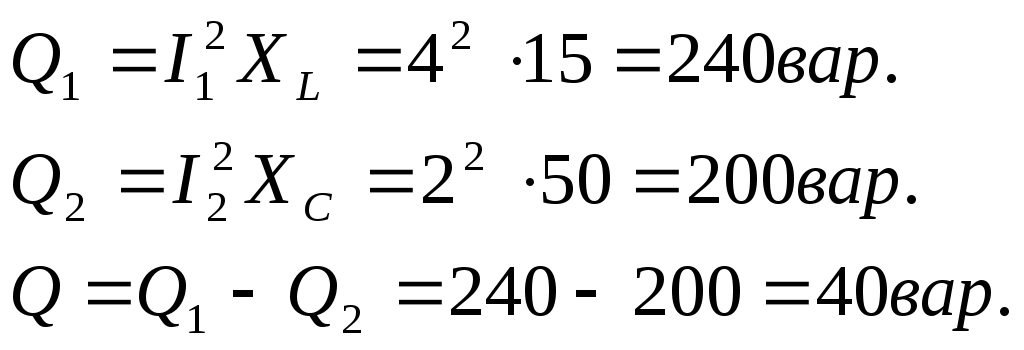
   

Обращаем внимание на то, что реактивная мощность конденсатора имеет обратный знак по сравнению с реактивной мощностью катушки.

7. 
   Полная мощность цепи:
   

Для построения векторной диаграммы задаемся масштабами по току в 1 см – 1А; по напряжению в 1 см – 25В. Построение диаграммы начинаем с вектора напряжения . Под углом ₁ к нему (в сторону отставания) откладываем в принятом масштабе вектор тока ; под углом ₂ (в сторону опережения) – вектор тока . Геометрическая сумма этих векторов представляет ток в неразветвленной части цепи. Проекции токов ветвей на вектор напряжения являются активными составляющими I_a1 и I_a2; проекции этих токов на вектор, перпендикулярный вектору напряжения, - реактивными составляющими I_p1 и I_p2
5

1 Начертите схему, согласно своему варианту (таблица 1)

2 Используя значения таблицы 1, запишите исходные данные согласно своему варианту.

3 Определите следующие величины, если они не заданы:

-ток по всех ветвях цепи;

-углы сдвига фаз (величину и знак);

-активную Р, реактивную Q, и полную S мощности, потребляемые цепью;

4 Начертите в масштабе векторную диаграмму токов

Таблица 1 – Исходные данные

№ варианта	U	R	XL	XC	№ схемы
	В	Ом	Ом	Ом
1	220	10	50	70	1
2	220	40	45	8	2
3	100	1	15	10	3
4	110	2	15	20	4
5	120	3	18	4	5
6	130	1	15	10	6
7	150	5	20	17	7
8	200	2	15	9	8
9	110	6	12	10	9
10	115	6	15	9	10
11	110	3	15	20	11
12	220	40	8	45	12
13	100	1	15	10	13
14	110	2	20	15	14
15	120	3	18	14	15
16	130	1	15	10	16
17	150	5	20	17	17
18	220	2	15	9	18
19	110	6	12	10	19
20	115	6	15	9	20
21	110	3	20	15	21
22	220	40	8	48	22
23	100	1	15	10	23
24	110	2	15	20	24
25	120	3	18	14	25
26	130	1	15	10	26
27	150	5	20	17	27
28	200	2	15	9	28
29	110	6	12	10	29
30	115	6	15	9	30

Пример 2. В схеме рис.А закон изменения ЭДС e = 141sin*ωt. Сопротивления R1 = 3 Ом, R2 = 2 Ом, L = 38,22 мГн, С = 1061,6 мкФ. Частота f = 50 Гц. Решить символическим методом. Найти ток и напряжения на элементах. Проверить 2-ой закон Кирхгофа для цепи.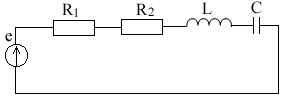



Рис.А. Схема с последовательным соединением элементов

Составляем комплексную схему, обозначив комплексные токи и напряжения (рис.Б):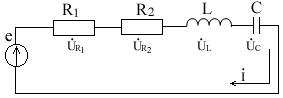



Рис.Б. Схема с комплексными обозначениями

По закону Ома ток в цепи равен



где U — комплексное входное напряжение, Z — полное сопротивление всей цепи. Комплекс входного напряжения находим как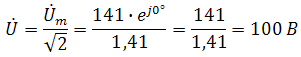



Пояснение: здесь начальная фаза φ = 0°, так как  общее выражение для мгновенного значения напряжение вида  приφ = 0° равно



Соответственно, комплекс входного напряжения в показательной форме запишется как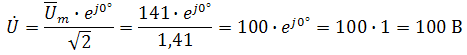



Полное комплексное сопротивление цепи в общем виде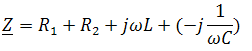



Находим комплексное сопротивление индуктивности



Находим комплексное сопротивление емкости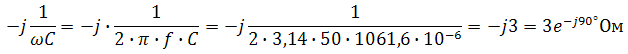



Соответственно, общее комплексное сопротивление цепи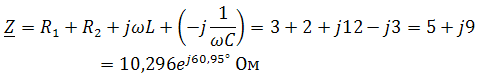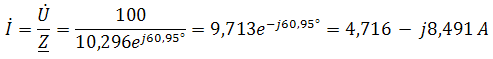



Ток в цепи



Комплексные напряжения на элементах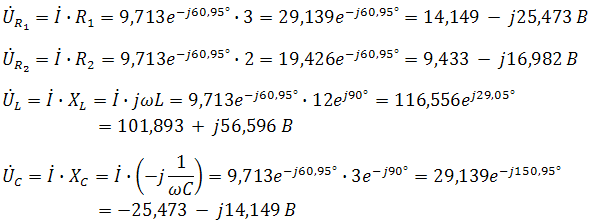



Проверяем второй закон Кирхгофа для замкнутого контура, т.е. должно выполняться равенство 

Проверяем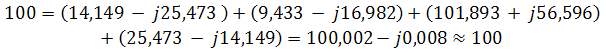



С небольшим расхождением из-за округлений промежуточных вычислений всё верно.

Пример 3.В электрической цепи (рис.С) однофазного синусоидального тока, схема и параметры элементов которой заданы для каждого варианта в таблице, определить:
1)  полное сопротивление электрической цепи и его характер;
2)  действующие значения токов в ветвях;
3) показания вольтметра и ваттметра;

1. 
   
   

Исходные данные: Е = 220 В, f = 50 Гц, L1 = 38,2 мГн, R2 = 6 Ом, С2 = 318 мкФ, L2 = 47,7 мГн, R3 = 10 Ом, С3 = 300 мкФ.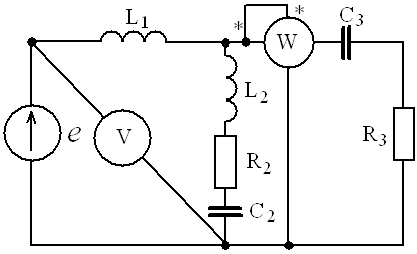



Рис.С.Цепь однофвзного синусоидального тока

Решение:
1.  Находим комплексные сопротивления ветвей и всей цепи:
Учитываем, что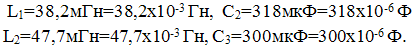



Комплексное сопротивление первой ветви:



Комплексное сопротивление второй ветви: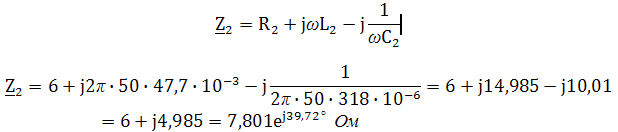



Комплексное сопротивление третьей ветви: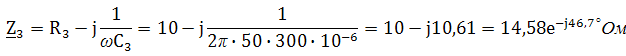



Общее сопротивление цепи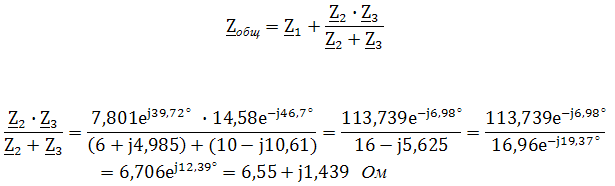



Откуда



— нагрузка носит активно-индуктивный характер

2. Находим действующие значения токов в ветвях: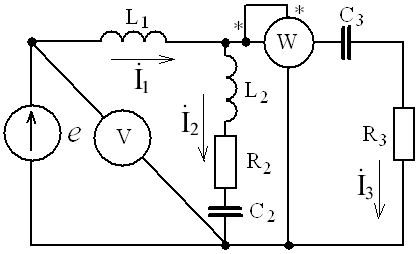

 



Рис.D. Схема с обозначенными комплексными токами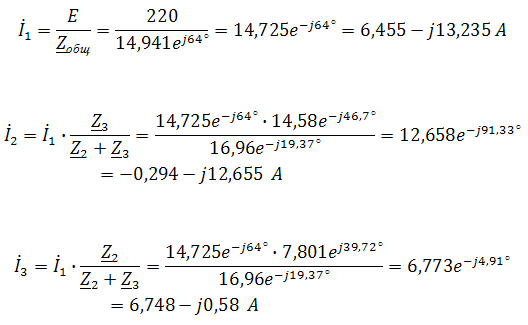



Действующие значения, соответственно,



3. Определим показания приборов:
Вольтметр подключен по схеме параллельно источнику питания. Соответственно его показание равно:
U=220 В
Ваттметр включен токовой обмоткой в разрыв третьей ветви, а обмоткой напряжения также к выводам третьей ветви, измеряя, таким образом,  активную мощность третьей ветви. Эта мощность равна мощности на сопротивлении R3. Его показания: