контрольная работа. Контрольная работа 1, вариант 6. Решение. По рисунку определяем координаты векторов и . Найдём разность векторов и

• Название: Решение. По рисунку определяем координаты векторов и . Найдём разность векторов и
• Анкор: контрольная работа
• Дата: 27.01.2023
• Размер: 460.84 Kb.
• Имя файла: Контрольная работа 1, вариант 6.docx
• Тип: Решение; #908024

6.1. Найти модуль разности векторов |a – b| и косинус угла  между векторами a и b.

Ответ округлить до двух значащих цифр.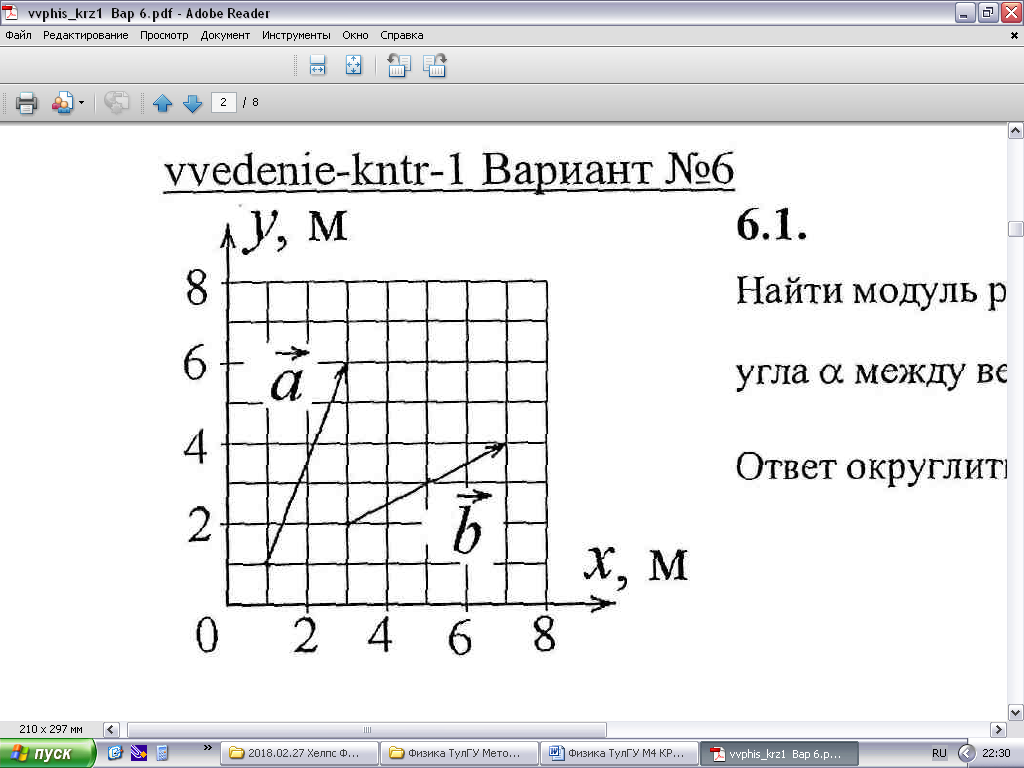



Решение.

По рисунку определяем координаты векторов и :

, .

Найдём разность векторов и :

.

Вычислим модуль разности векторов и :

.

Найдём скалярное произведение векторов и :

.

Найдём модули векторов и :

;

.

Вычислим косинус угла между векторами и :

.

Ответ: , .

6.2. Найти модуль суммы векторов |a + b| и модуль векторного произведения |[axb]|.

Ответ округлить до двух значащих цифр.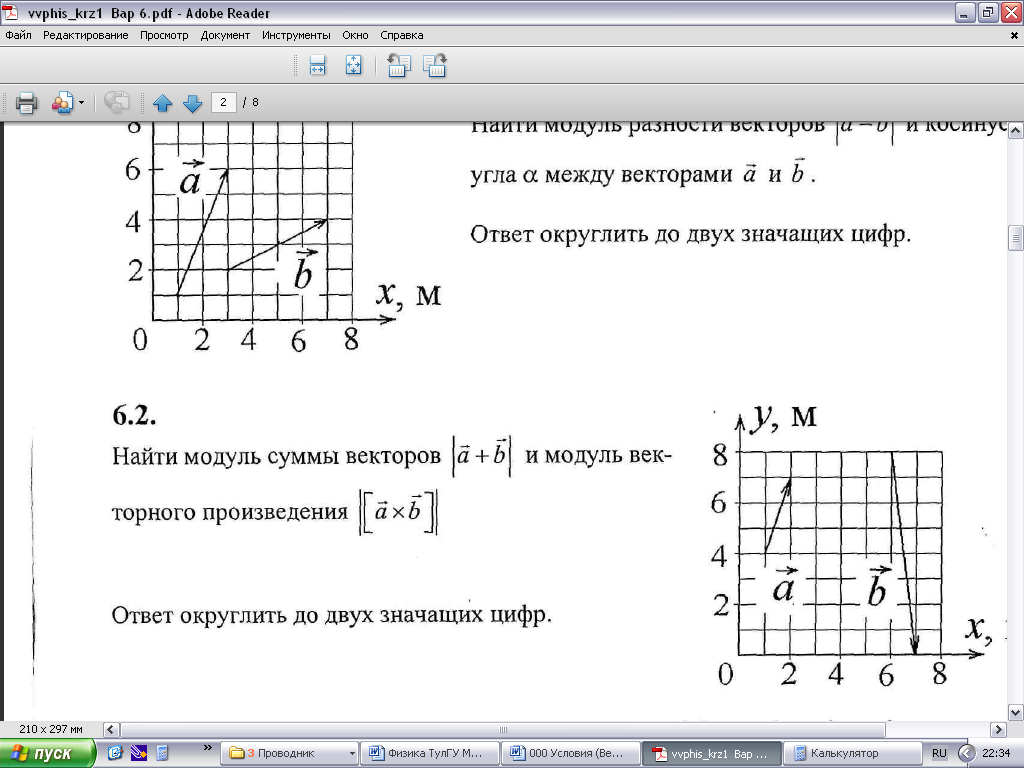


Решение.

По рисунку определяем координаты векторов и :

, .

Найдём сумму векторов и :

.

Вычислим модуль суммы векторов и :

.

Найдём модуль векторного произведения векторов и :

.

Ответ: , .

6.3. Найти значение производной от функции

f(x) = sin(cosx) + 4x⁵

в точке с координатой x = 1.

Решение.

Найдём производную заданной функции, используя правила дифференцирования и таблицу производных:

;

;

;

.

Вычислим значение производной в точке :

.

Ответ: .

6.4. Найти частные производные z`<sub>x</sub> и z`_y функции

z = ln(x² + y).

Решение.

Частную производную по найдём, считая переменную постоянной:



Частную производную по найдём, считая переменную постоянной:



Ответ: , .

6.5. Найти градиент функции u = f(x,y,z) в точке M.

u = ln(3 – x²) + xy²z, M(1; 3; 2).

Решение.

Вектор-градиент скалярного поля u = f(x,y,z) равен:

.

Найдём значения частных производных функции в точке M:

,

;

,

;

,

.

Запишем градиент скалярного поля u в точке М:

.

Ответ: .