Статистика 02.08.22. Решение Показатели центра распределения средняя арифметическая, мода и медиана

• Название: Решение Показатели центра распределения средняя арифметическая, мода и медиана
• Дата: 29.09.2022
• Размер: 26.62 Kb.
• Имя файла: Статистика 02.08.22.docx
• Тип: Решение; #705669

Задача 1
Условие:

В целях расширения ассортимента туристических услуг были получены следующие данные, таблица 1.
Таблица 1 – Исходные данные

Дополнительные расходы туристов, у.е	10-20	20-30	30-40	40-50	50-60
Число туристов, чел.	8	30	60	32	10

Определить показатели центра распределения и сделать выводы.
Решение:

Показатели центра распределения – средняя арифметическая, мода и медиана.

Средняя величина по интервальному ряду распределения определяется по формуле средней арифметической взвешенной.

,

где x_i – индивидуальные значения осредняемого признака:

f_i – частота повторения признака в совокупности.

Чтобы применить эту формулу, необходимо варианты признака выразить одним числом (дискретным). За такое дискретное число принимается средняя арифметическая простая из верхнего и нижнего значения интервала.

Для первой группы дискретная величина х будет равна:

х=

Аналогично рассчитывается для других групп.

Составим расчетную таблицу 2.

Таблица 2 – Расчетная таблица

Группы	Середина интервала (х)	Количество fi	xifi	Накопленная частота
10-20	15	8	120	8
20-30	25	30	750	38
30-40	35	60	2100	98
40-50	45	32	1440	130
50-60	55	10	550	140
Итого		140	4960

Средняя взвешенная:

у.е.

Мода - наиболее часто встречающееся значение признака у единиц данной совокупности.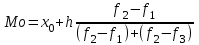



где x₀ – начало модального интервала; h – величина интервала; f₂ –частота, соответствующая модальному интервалу; f₁ – предмодальная частота; f₃ – послемодальная частота.

Выбираем в качестве начала интервала 30, так как именно на этот интервал приходится наибольшее количество.

у.е

Наиболее часто встречающееся значение ряда – 35,172 у.е

Медиана делит выборку на две части: половина вариант меньше медианы, половина — больше.

Медиана соответствует варианту, стоящему в середине ранжированного ряда. Медианным является интервал 30 - 40, т.к. в этом интервале накопленная частота S, больше медианного номера (медианным называется первый интервал, накопленная частота S которого превышает половину общей суммы частот).

Ме=

у.е.

Таким образом, 50% единиц совокупности будут меньше по величине 35,33 у.е.

Среднее значение примерно равно моде и медиане, что свидетельствует о нормальном распределении выборки.