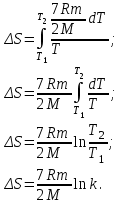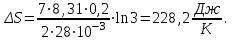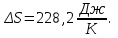|
|
Решение Поскольку процесс 12 изохорный, то Запишем уравнение Менделеева Клапейрона для первого состояния азота
Вариант 3.
Задание 5.
Задача 1.
Один моль идеального газа переходит из начального состояния 1 в конечное состояние 3 в результате двух изохорного 1-2 и адиабатного 2-3 процессов. Значения давления и объема газа в состояниях 1 и 3 равны соответственно 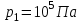 , , 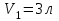 и и 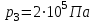 , , 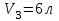 . Найти работу A, совершенную газом, количество теплоты Q, полученное газом и приращение внутренней энергии газа . Найти работу A, совершенную газом, количество теплоты Q, полученное газом и приращение внутренней энергии газа 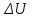 в процессе перехода из начального состояния 1 в конечное состояние 3. в процессе перехода из начального состояния 1 в конечное состояние 3.
Дано:
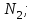
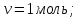
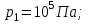
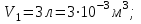
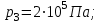
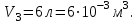
|
Решение:
Поскольку процесс 1-2 изохорный, то 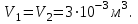
Запишем уравнение Менделеева – Клапейрона для первого состояния азота:
 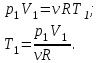
Где 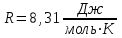 - универсальная газовая постоянная. - универсальная газовая постоянная.
Подставим численные значения и произведём вычисления температуры азота в первом состоянии:
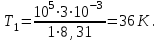
Запишем уравнение Менделеева – Клапейрона для третьего состояния азота:
 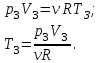
Подставим численные значения и произведём вычисления температуры азота в третьем состоянии:
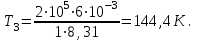
Поскольку процесс 2-3 адиабатный, то по формуле Пуассона, получаем:
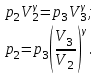
|
Найти:
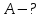
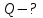
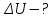
|
Где 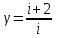 - показатель адиабаты, - показатель адиабаты, 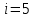 - степень свободы молекул двухатомного газа. - степень свободы молекул двухатомного газа.
Следовательно:
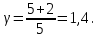
Подставим численные значения и произведём вычисления:
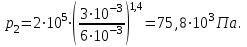
Применяя закон Гей - Люссака для изобарного процесса 1 – 2 можно записать:
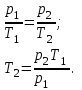
Подставим численные значения и произведём вычисления температуры азота во втором состоянии:
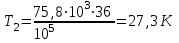
Для проведения дальнейших расчётов, запишем параметры газа в каждой точке.
В 1-й точке - 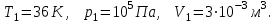
Во 2-й точке - 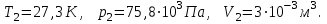
В 3- й точке - 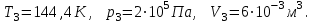
Вычисляем приращение внутренней энергии газа в процессе 1-2:
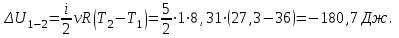
Вычисляем приращение внутренней энергии газа в процессе 2-3:
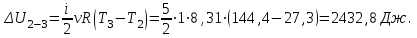
Вычисляем приращение внутренней энергии газа 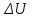 в процессе перехода из начального состояния 1 в конечное состояние 3. в процессе перехода из начального состояния 1 в конечное состояние 3.
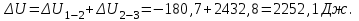
Работа газа в изохорном процессе равна нулю 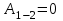 . .
Вычисляем работу газа в процессе 2-3, применяя первый закон термодинамики, учитывая, что в адиабатном процессе 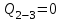 : :
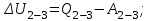
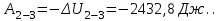
Вычисляем работу A, совершенную газом в процессе перехода из начального состояния 1 в конечное состояние 3.
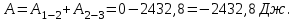
Вычисляем количество теплоты 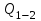 , полученное газом в процессе 1-2, применяя первый закон термодинамики: , полученное газом в процессе 1-2, применяя первый закон термодинамики:
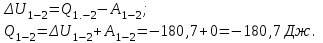
Вычисляем количество теплоты Q, полученное газом в процессе перехода из начального состояния 1 в конечное состояние 3.
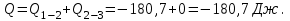
Ответ: 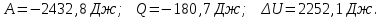
|
Задача 2.
Идеальный газ -  совершает замкнутый цикл, состоящий из трех процессов: изобарного 1 - 2, адиабатного 2 - 3 и изотермического 3 - 1, идущий по часовой стрелке. Значения давления и объёма газа в состояниях 1, 2 и 3 равны соответственно совершает замкнутый цикл, состоящий из трех процессов: изобарного 1 - 2, адиабатного 2 - 3 и изотермического 3 - 1, идущий по часовой стрелке. Значения давления и объёма газа в состояниях 1, 2 и 3 равны соответственно 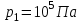 , , 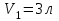 , и , и 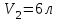 . Найти термический к.п.д. цикла. . Найти термический к.п.д. цикла.
Дано:
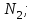
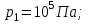
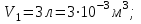
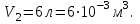
|
Решение:
КПД цикла вычисляется по формуле:
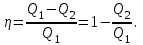
Где 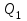 - количество теплоты, переданное газу за цикл от нагревателя; - количество теплоты, переданное газу за цикл от нагревателя; 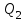 - количество теплоты, отданое газом за цикл холодильнику. - количество теплоты, отданое газом за цикл холодильнику.
Работа газа при изобарном процессе вычисляется по формуле:
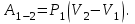
Подставим численные значения и произведём вычисления:
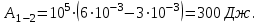
Изменение внутренней энергии в процессе 1 – 2 вычмсляется по формуле:
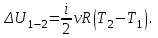
Применим уравнение Менделеева - Клапейрона для первого и второго состояний газа:
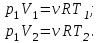
Где 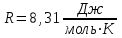 - универсальная газовая постоянная, - универсальная газовая постоянная, 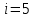 - степень свободы молекул двухатомного газа. - степень свободы молекул двухатомного газа.
Находим разность второго и первого уравнений:
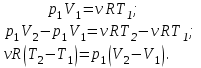
После подстановки в формулу изменения внутренней энергии, получаем:
|
Найти:
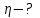
|
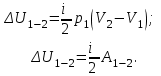
Вычисляем количество теплоты 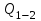 , полученное газом в процессе 1-2, применяя первый закон термодинамики: , полученное газом в процессе 1-2, применяя первый закон термодинамики:
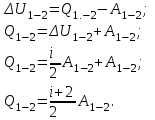
Подставим численные значения и произведём вычисления:
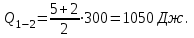
В адиабатном процессе 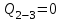 : :
Учитывая, что для изотермического процесса 3 – 1 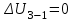 , по первому закону термодинамики, получаем: , по первому закону термодинамики, получаем:
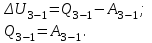
Работа газа при изотермическом процессе вычисляется по формуле:
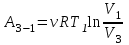 . .
Согласно уравнению Менделеева – Клапейрона для первого состояния газа, получаем:
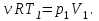
После подстановки, получаем:
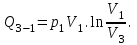
Найдём объём азота 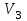 для третьего состояния. для третьего состояния.
Для изобарного процесса 1 – 2 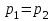 . .
Для изотермического процесса 3 – 1, имеем:
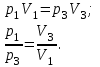
Для адиабатного процесса 2 – 3, получаем:
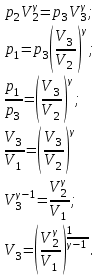
Где 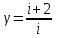 - показатель адиабаты. - показатель адиабаты.
Следовательно:
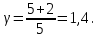
Подставим численные значения и произведём вычисления объём азота 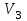 для третьего состояния: для третьего состояния:
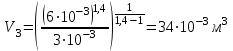
Подставим численные значения и произведём вычисления  : :
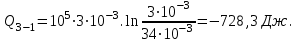
Количество теплоты, полученное газом за цикл от нагревателя:
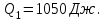
Количество теплоты, отданое газом за цикл холодильнику:
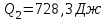
Теперь вычисляем КПД цикла:
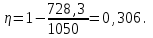
Ответ: 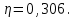
|
Задача 3.
Идеальный газ - 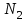 массой массой 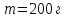 совершает политропный процесс. Молярная теплоемкость газа в этом процессе совершает политропный процесс. Молярная теплоемкость газа в этом процессе 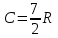 , где R – универсальная газовая постоянная. Абсолютная температура газа в результате данного процесса возрастает в , где R – универсальная газовая постоянная. Абсолютная температура газа в результате данного процесса возрастает в 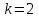 раз. Найти приращение энтропии газа раз. Найти приращение энтропии газа 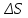 в результате данного процесса. в результате данного процесса.
Дано:
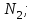
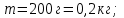
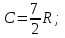
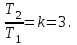
|
Решение:
Приращение энтропии идеального газа вычисляется по формуле:
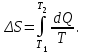
При политропном процессе (с постоянной теплоёмкостью):
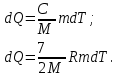
Где 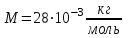 - молярная масса азота, - молярная масса азота, 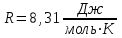 - универсальная газовая постоянная. - универсальная газовая постоянная.
Подставляя последнее уравнение в уравнение для приращения энтропии, получаем:
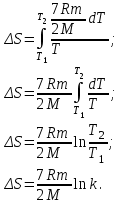
Подставим численные значения и произведём вычисления:
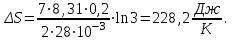
Ответ: 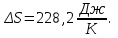
| |
|
|
 Скачать 178.9 Kb.
Скачать 178.9 Kb.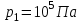 ,
, 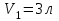 и
и 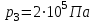 ,
, 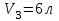 . Найти работу A, совершенную газом, количество теплоты Q, полученное газом и приращение внутренней энергии газа
. Найти работу A, совершенную газом, количество теплоты Q, полученное газом и приращение внутренней энергии газа 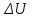 в процессе перехода из начального состояния 1 в конечное состояние 3.
в процессе перехода из начального состояния 1 в конечное состояние 3.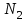 совершает замкнутый цикл, состоящий из трех процессов: изобарного 1 - 2, адиабатного 2 - 3 и изотермического 3 - 1, идущий по часовой стрелке. Значения давления и объёма газа в состояниях 1, 2 и 3 равны соответственно
совершает замкнутый цикл, состоящий из трех процессов: изобарного 1 - 2, адиабатного 2 - 3 и изотермического 3 - 1, идущий по часовой стрелке. Значения давления и объёма газа в состояниях 1, 2 и 3 равны соответственно 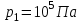 ,
, 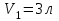 , и
, и 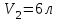 . Найти термический к.п.д. цикла.
. Найти термический к.п.д. цикла.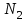 массой
массой 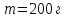 совершает политропный процесс. Молярная теплоемкость газа в этом процессе
совершает политропный процесс. Молярная теплоемкость газа в этом процессе 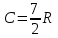 , где R – универсальная газовая постоянная. Абсолютная температура газа в результате данного процесса возрастает в
, где R – универсальная газовая постоянная. Абсолютная температура газа в результате данного процесса возрастает в 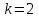 раз. Найти приращение энтропии газа
раз. Найти приращение энтропии газа 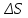 в результате данного процесса.
в результате данного процесса.
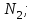
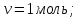
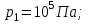
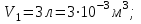
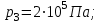
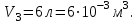
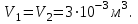

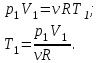
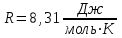 - универсальная газовая постоянная.
- универсальная газовая постоянная.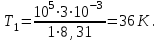
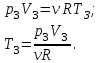
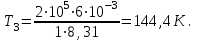
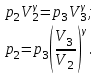
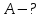
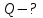
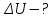
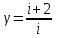 - показатель адиабаты,
- показатель адиабаты, 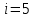 - степень свободы молекул двухатомного газа.
- степень свободы молекул двухатомного газа.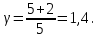
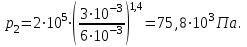
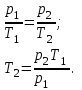
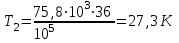
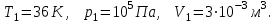
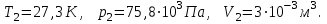
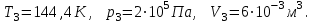
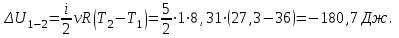
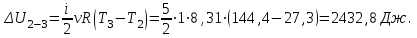
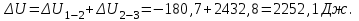
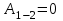 .
.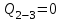 :
: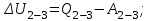
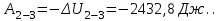
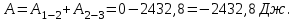
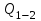 , полученное газом в процессе 1-2, применяя первый закон термодинамики:
, полученное газом в процессе 1-2, применяя первый закон термодинамики: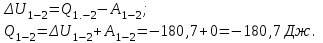
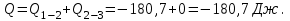
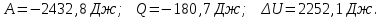
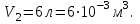
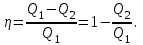
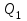 - количество теплоты,
- количество теплоты, 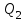 - количество теплоты, отданое газом за цикл холодильнику.
- количество теплоты, отданое газом за цикл холодильнику.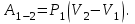
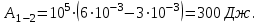
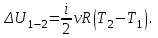
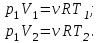
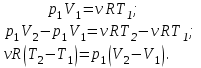
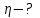
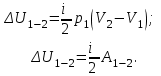
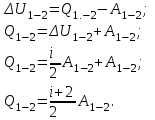
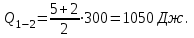
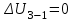 , по
, по 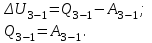
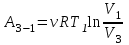 .
.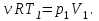
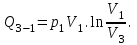
 для третьего состояния.
для третьего состояния.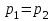 .
.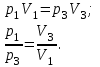
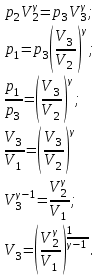
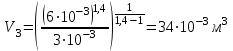
 :
: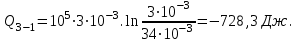
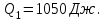
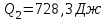
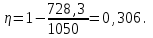
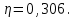
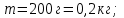
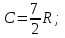
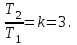
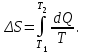
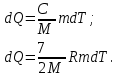
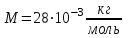 - молярная масса азота,
- молярная масса азота,