Решение Построим область интегрирования
 Скачать 130.5 Kb.
|
|
Вариант № 1: 1.Изменить порядок интегрирования и вычислить интеграл  , если область D ограничена линиями  ,  ,  ,  Решение: Построим область интегрирования: 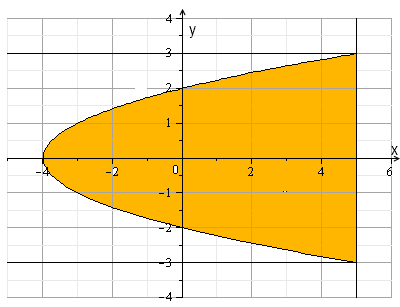 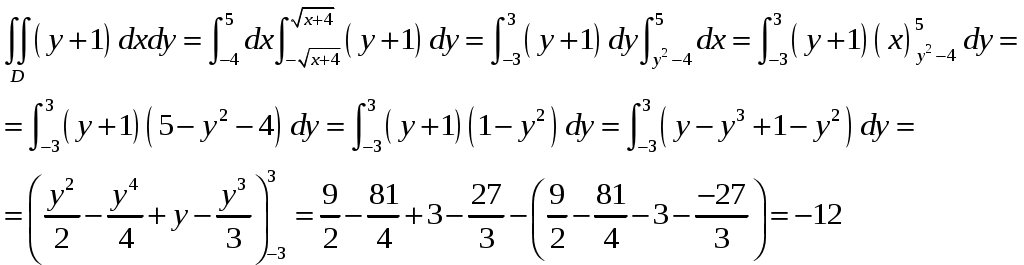 2.Проверить формулу Грина для интеграла  , где L-контур  А(0;0), В(3;0), С(0;6).Решение: Формула Грина:  .Построим треугольник АВС: 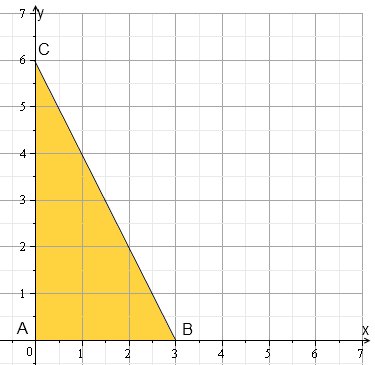 Составим уравнения сторон треугольника: 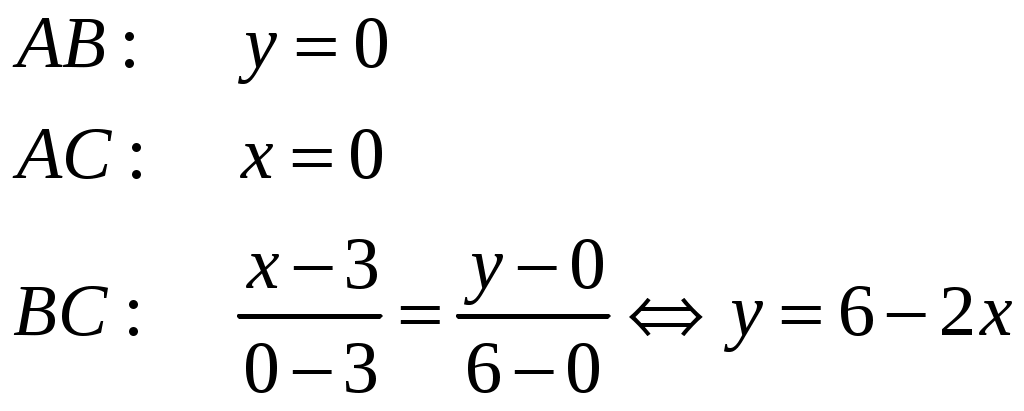 Нужно вычислить интеграл .Тогда 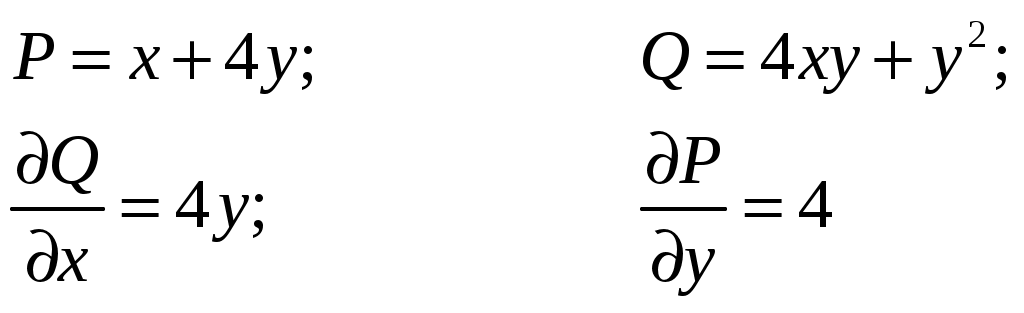 С одной стороны: 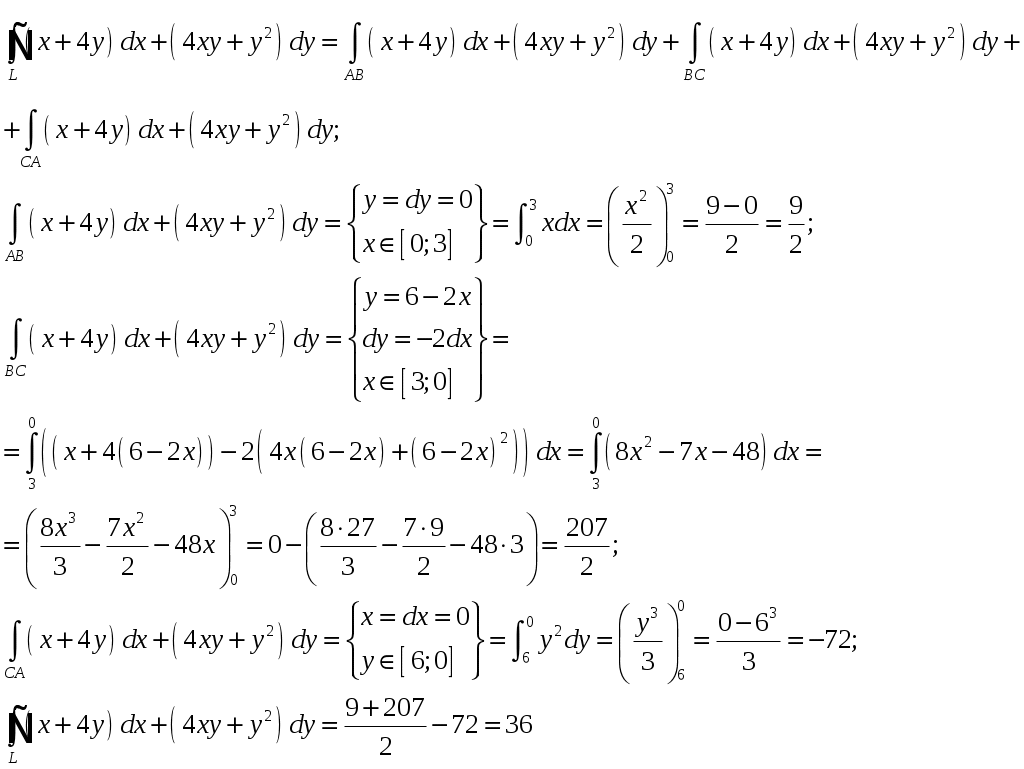 С другой стороны: 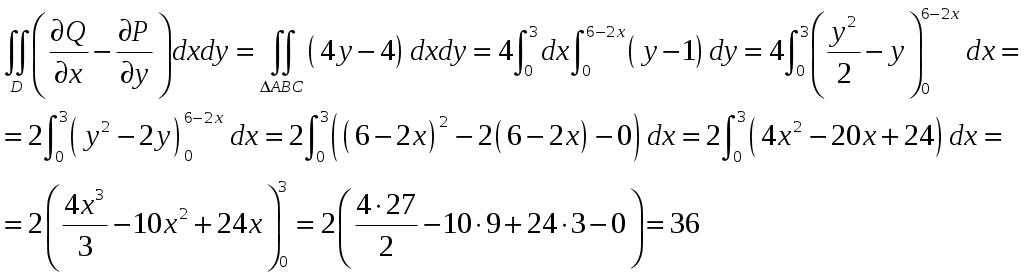 Обе формулы привели к одному и тому же результату. Формула проверена. 3.Исследовать на сходимость ряды:      Решение: По необходимому признаку сходимости ряд расходится: 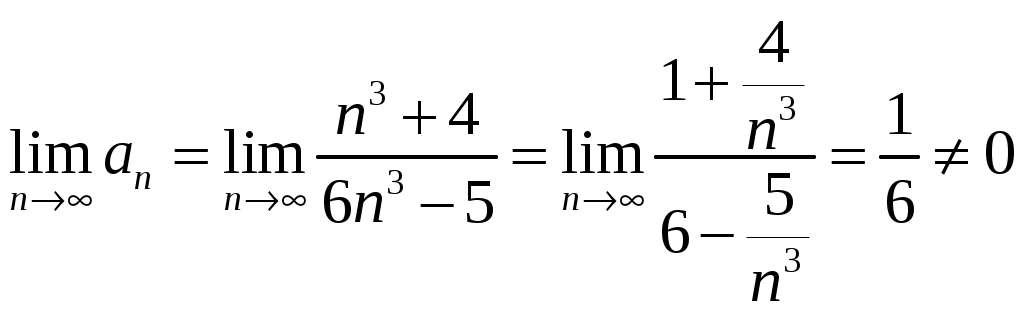 . По интегральному признаку: 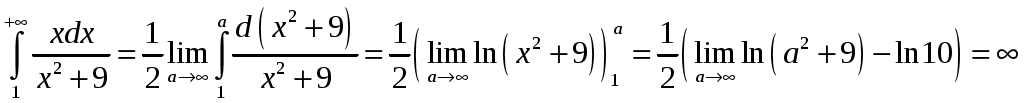 .Ряд расходится. По интегральному признаку: 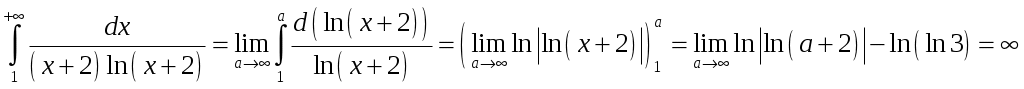 Ряд расходится. Данный ряд сходится условно по признаку Лейбница: последовательность 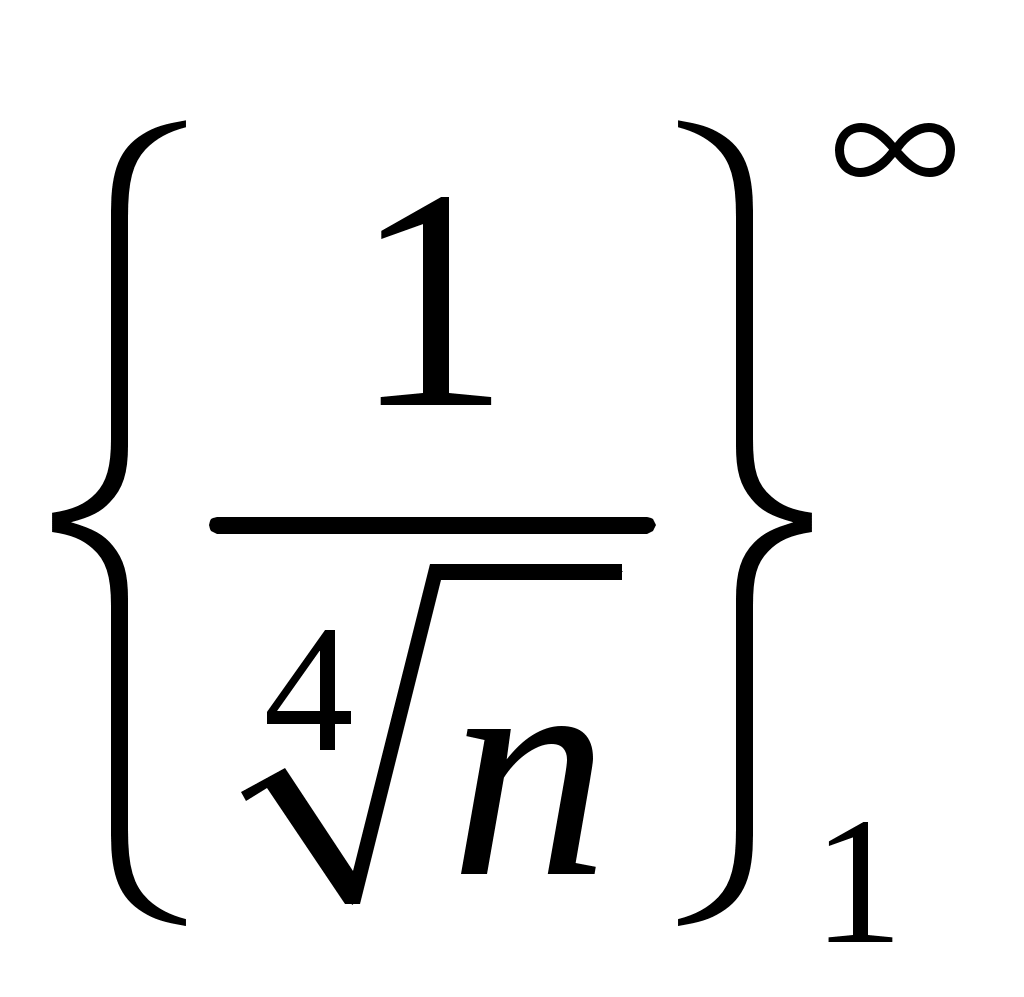 монотонно убывает к 0.Абсолютной сходимости нет, так как ряд  расходится. Ряд сходится абсолютно по признаку сравнения в предельной форме: 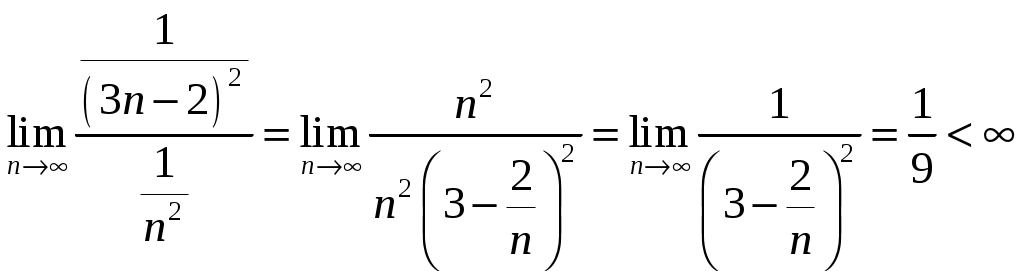 : .При этом ряд  сходится.4. Найти область сходимости степенного ряда  Решение: По признаку Даламбера: 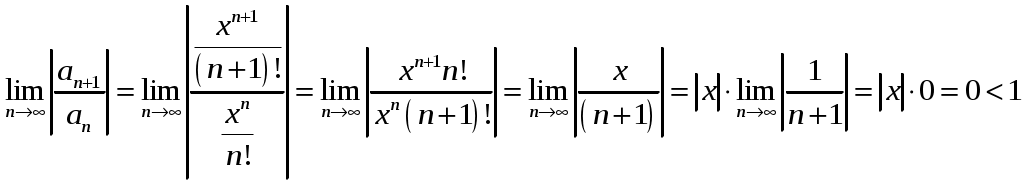 .Тогда данный ряд сходится на всей числовой прямой. 5.Вычислить с заданной степенью точности   ( =0,001)Решение: Известно разложение:  .Тогда 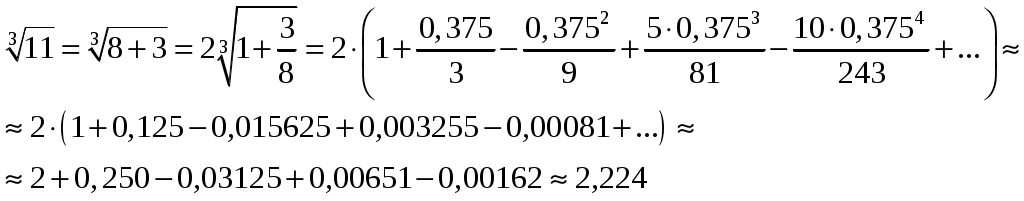 |