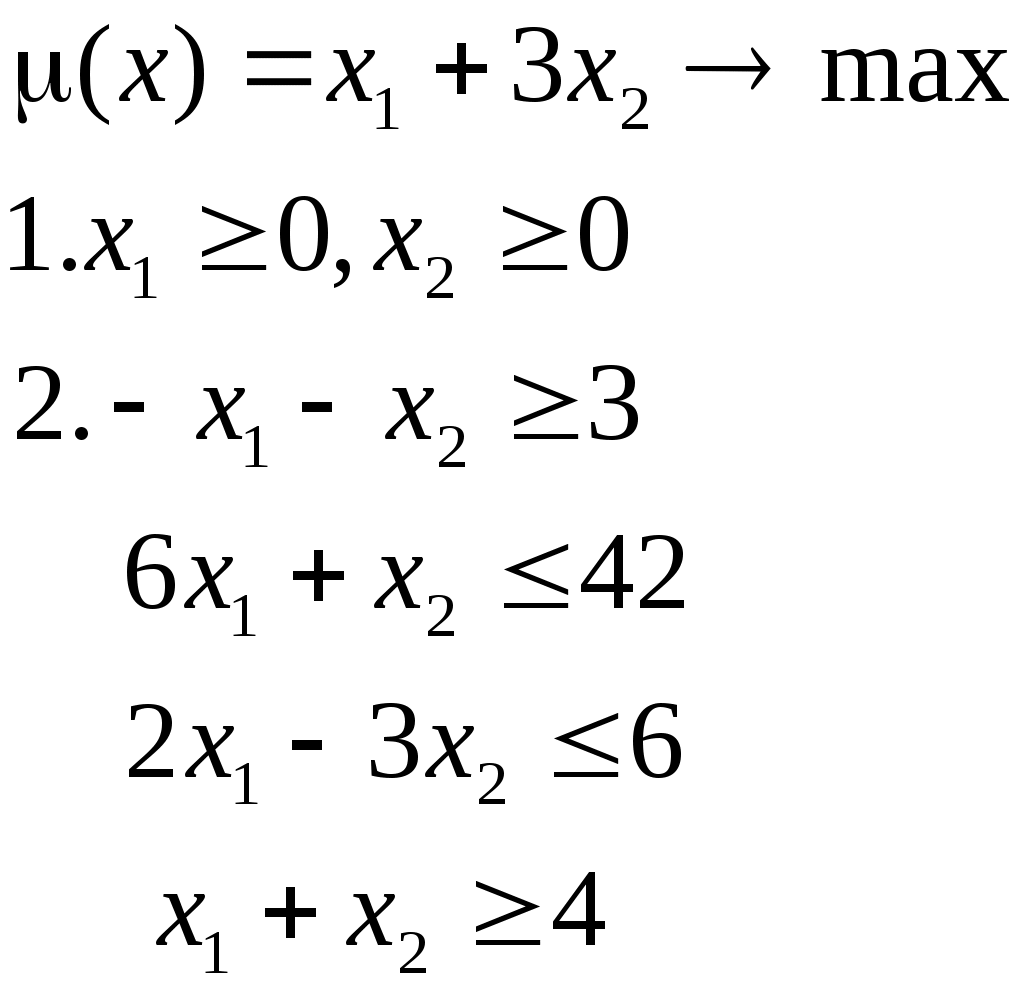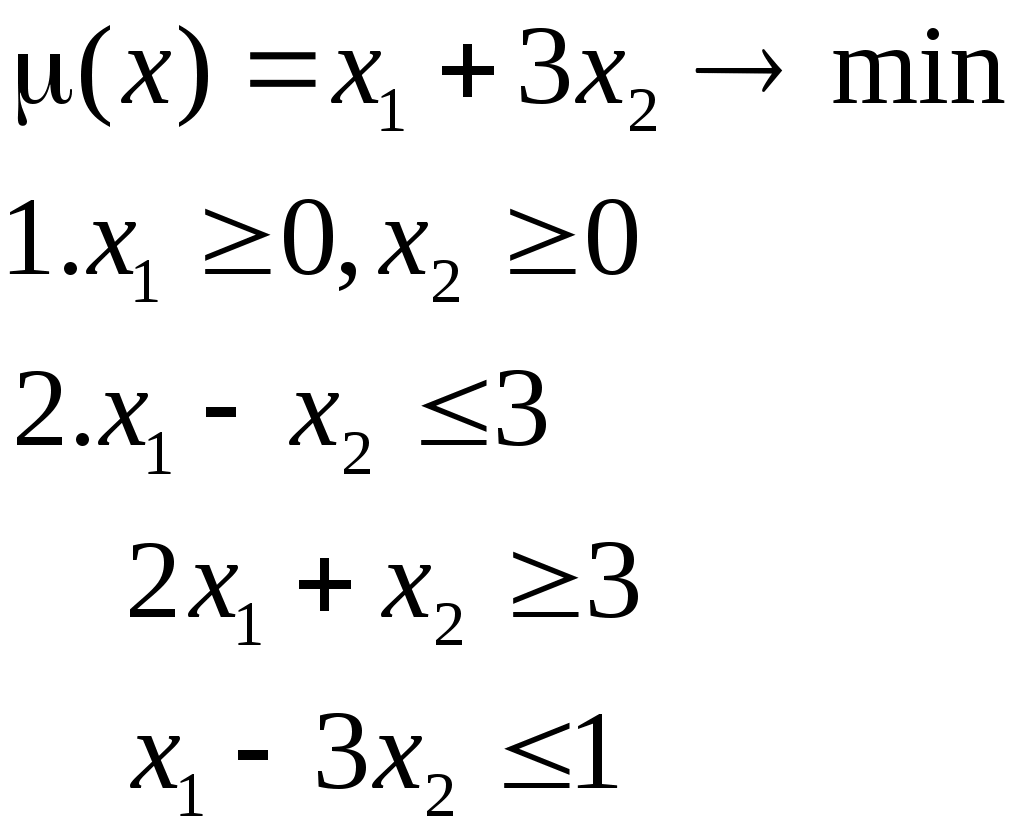Практика. Практика_1_МО3 (1). Решение. Построим одр Строим прямые, уравнения которых получаются в результате

• Название: Решение. Построим одр Строим прямые, уравнения которых получаются в результате
• Анкор: Практика
• Дата: 27.10.2021
• Размер: 261 Kb.
• Имя файла: Практика_1_МО3 (1).doc
• Тип: Решение; #257328

Практика №1. Графический метод решения задач линейного программирования

Примеры решения задач линейного программирования графическим методом

Пример 1.

Решение.

1. 
   Построим ОДР:
   

1.1. Строим прямые, уравнения которых получаются в результате

замены знаков неравенств в ограничении 2 на знаки

равенств (рис. 5):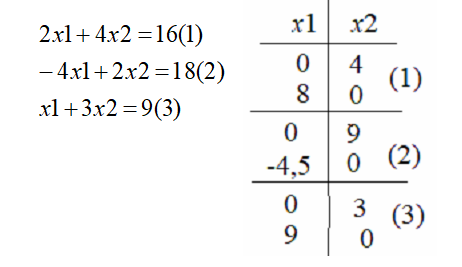





Рис. 5. Построение прямых – границ ОДР
1.2. Находим полуплоскости, определяемые каждым

неравенством ограничения 2 и ОДР (рис. 6, 7).



Рис. 6. Построение полуплоскостей по ограничениям (2)
ОДР – это треугольник АВС, выпуклое множество (рис. 7), вершины А, В, С – угловые точки, в одной из которых достигается оптимальное решение.



Рис. 7. Построение ОДР – треугольник АВС

2. 
   Строится вектор , линии уровня , где – любое число. Линии уровня передвигаются по ОДР в направлении вектора и перпендикулярно ему до тех пор, пока линии уровня и ОДР не пересекутся хотя бы в одной точке.
   

Рис. 8. Построение линий уровня с разными значениями в направлении вектора

3. 
   Точка пересечения ОДР и линии уровня – угловая точка С – оптимальное решение вектор :
   

Решим систему из уравнений (1) и (3) для нахождения угловой точки С:

4. 
   Подставив найденное решение в целевую функцию
   

, получим ее максимальное значение.

Минимальное значение целевой функции (линии уровня

проводятся в направлении, противоположном вектору

) достигается в угловой точке А(0,3), минимальное значение целевой функции .

Пример 2.

Решение.

5. 
   Построим ОДР:
   

1.1. Строим прямые, уравнения которых получаются в результате

замены знаков неравенств в ограничении 2 на знаки

равенств (рис. 9):




Рис. 9. Построение прямых – границ ОДР
1.2. Находим полуплоскости, определяемые каждым

неравенством ограничения 2 и ОДР (рис. 10, 11):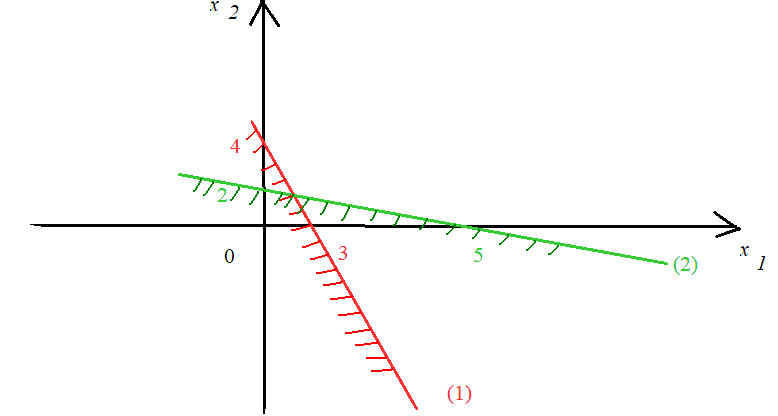



Рис. 10. Построение полуплоскостей по ограничениям (2)
ОДР – это четырехугольник ОАВС, выпуклое множество (рис. 11), вершины О, А, В, С – угловые точки, в одной из которых достигается оптимальное решение.



Рис. 11. Построение ОДР – четырехугольник ОАВС

6. 
   Строится вектор , линии уровня , где – любое число. Линии уровня передвигаются по ОДР в направлении вектора до тех пор, пока линии уровня и ОДР не пересекутся хотя бы в одной точке (рис. 12).
   

Рис. 12. Построение линий уровня с

разными значениями в направлении вектора

7. 
   Пересечение линий уровня и ОДР – отрезок . Оптимальное решение – любая точка этого отрезка (задача имеет множество оптимальных решений):
   

1.3. Задания для самостоятельной работы: решить графически задачи линейного программирования

Задача 1. Задача 3. Задача 5.

Задача 2. Задача 4. Задача 6.