Электрическое поле образовано заряженной нитью, длиной L=0,2 м и линейной плотностью τ=〖10〗^(-9) Клм. Вычислить разность потенци. Задача 61. Решение Потенциал поля от равномерно заряженной нити
 Скачать 33.9 Kb. Скачать 33.9 Kb.
|
|
Задача 61. 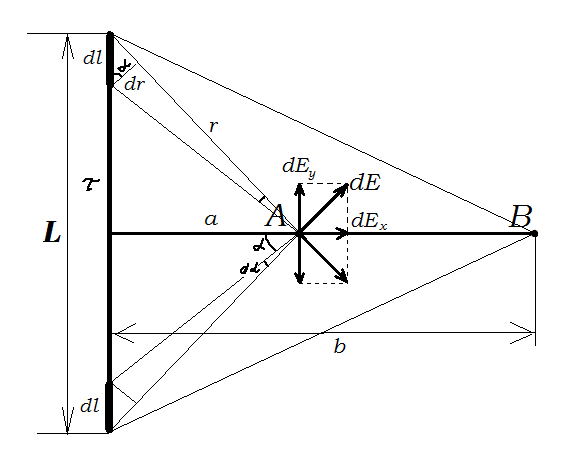 Электрическое поле образовано заряженной нитью, длиной L=0,2 м и линейной плотностью Электрическое поле образовано заряженной нитью, длиной L=0,2 м и линейной плотностью 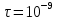 Кл/м. Вычислить разность потенциалов в двух точках, лежащих на перпендикуляре, проведённом через середину нити, на расстояниях А=0,1 м и В=0,25 м от нити. Кл/м. Вычислить разность потенциалов в двух точках, лежащих на перпендикуляре, проведённом через середину нити, на расстояниях А=0,1 м и В=0,25 м от нити. Дано: Дано:l=0,2 м. 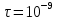 Кл/м. Кл/м.а=0,1 м.  b=0,25 м. b=0,25 м.U -? Решение: Потенциал поля от равномерно заряженной нити: 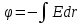 Разобьём бесконечно длинную нить на элементарные участки dℓ. Напряженность поля 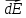 , создаваемого участком dℓ на расстоянии а от нити, можно разложить на две составляющие: , создаваемого участком dℓ на расстоянии а от нити, можно разложить на две составляющие: 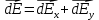 Так как точки лежат на серединном перпендикуляре, из принципа симметрии следует, что алгебраическая сумма проекций напряженностей поля на ось 0у равна нулю. Результирующее поле направлено вдоль оси 0х. Определим составляющую 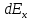 от элемента нити dl: от элемента нити dl: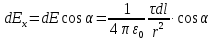 Как видно из рисунка: 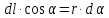 и и 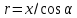 , где x- расстояние от нити до точки расположенной симметрично относительно её концов. Поэтому , где x- расстояние от нити до точки расположенной симметрично относительно её концов. Поэтому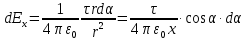 Проинтегрировав это выражение найдем E 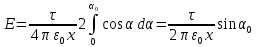 где 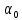 - максимальное значение угла - максимальное значение угла 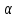 . .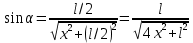 Отсюда 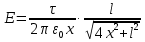 Разница потенциалов равна: 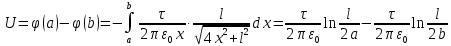 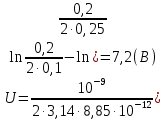 Ответ: U=7,2 B. |
