Задание 1 Теория спроса и предложения. Решение Представим функции спроса и предложения в виде прямых функций Для функции спроса уравнение принимает следующий вид
 Скачать 54.86 Kb. Скачать 54.86 Kb.
|
|
Вариант № 3 Pa = -0,02Qd + 100 Qa = 150 - 2Pd Ps = 0,030s + 20 Qs = 3Ps - 100 a) ставку акциза, дающего максимальную величину налоговых сборов; б) определить величину этих сборов; в) построить зависимость между налоговыми поступлениями и налоговой ставкой. Решение Представим функции спроса и предложения в виде прямых функций Для функции спроса уравнение принимает следующий вид: Pd = -0,02Qd + 100; 0,020Qd = 100 - P; Qd = 5000 - 50P Для функции предложения оно выражается как: Ps = 0,03Qs + 20; 0,03Qs = P - 20; Qs = 33P - 667. Найдём первоначальное равновесие на рынке. Приравняем функции спроса и предложения: Qd = Qs 5000 - 50P = 33P - 667 83P=5667 P=68 Рe = 68 - равновесная цена, Qe = 5000-50*68 = 1600 - равновесный объём. Изобразим ситуацию графически. Найдём координаты точек пересечения графиков функций с осью ординат. При Q = 0 функция спроса пересекает ось ординат в точке А. 5000 - 50P = 0 Р = 100 При Q = 0 функция предложения пересекает ось ординат в точке С: 33P – 667 = 0 Р = 20 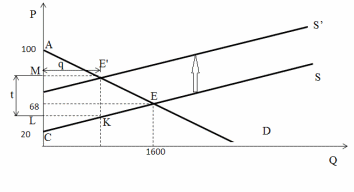 Если государство будет взимать акциз с каждой проданной единицы товара А, то кривая предложения сдвинется вверх на величину акциза в положение S’. Графически сумма налоговых сборов будет представлена площадью прямоугольника ME’KL, вписанного в треугольник АЕС. Чтобы найти максимальную сумму налога, необходимо найти функцию площади прямоугольника и решить задачу на максимум функции. Высота треугольника АЕС равна 1600, а основание (100 – 20) = 80 Пусть t, q – длины сторон прямоугольника. Боковая сторона прямоугольника КЕ’ отсекает ΔКЕ’E, подобный данному ΔAEC. Высоты в этих треугольниках пропорциональны основаниям, поэтому можно записать: (1600-q)/1600=t/80 t = (128000-80q)/1600 Площадь искомого прямоугольника ME’KL: S = t * q = (128000-80q)/1600*q=80q-0,05q2 Найдём максимум этой функции. Для этого определим её производную и приравняем её к нулю. S’ = 0 80 – 2 × 0,05q = 0 80 = 2 × 0,05q q = 800 Тогда наибольшее значение функции S при q = 800, равно: S = 80*800 – 0,05*8002 = 64000 – 32000 = 32000 Акциз при этом будет равен: t = S/q = 32000/800 = 40 Итак, максимальная сумма налоговых сборов равна 32000, при акцизе 40 с каждой проданной единицы товара. в) построить зависимость между налоговыми поступлениями и налоговой ставкой. Функция, определяющая зависимость между величиной налога и налоговыми поступлениями называется функцией Лаффера.  |
