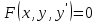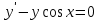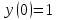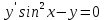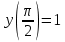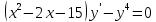Решение Представим уравнение в виде Интегрируем обе части уравнения

• Название: Решение Представим уравнение в виде Интегрируем обе части уравнения
• Дата: 23.04.2023
• Размер: 20.7 Kb.
• Имя файла: prakt_zadanie_1_v5.docx
• Тип: Решение; #1083314

Вариант 5
Задача 1:

Даны дифференциальные уравнения первого порядка с разделяющимися переменными и их начальные условия. Найти общие решения этих уравнений и определить частные решения.

Номер варианта		Начальное условие		Начальное условие
5	а)		б)

Решение:

1. 
   Представим уравнение в виде: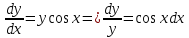
   

Интегрируем обе части уравнения: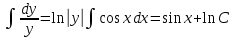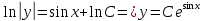





Найдем частное решение, удовлетворяющее начальным условиям: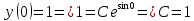



Решение задачи Коши: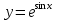

2. 
   Представим уравнение в виде: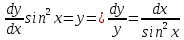
   

Интегрируем обе части уравнения: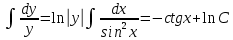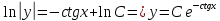





Найдем частное решение, удовлетворяющее начальным условиям: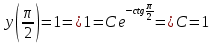



Решение задачи Коши: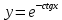



Ответ:

а)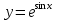

б)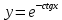

Задача 2:

Решить дифференциальное уравнение первого порядка.

№
5

Решение:

Запишем уравнение в виде: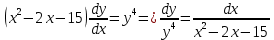



Интегрируем обе части уравнения: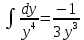





Разложим дробь на сумму простейших дробей, предварительно разложив знаменатель на множители: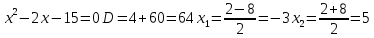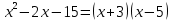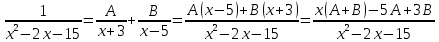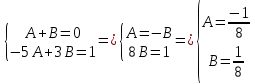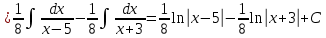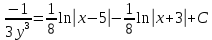













Общий интеграл уравнения: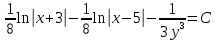


Ответ: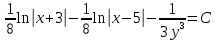