Решение. При решении воспользуемся методом, основанным на построении зон Френеля
 Скачать 0.64 Mb. Скачать 0.64 Mb.
|
|
Дифракция Френеля Примеры решения задач Пример 1. Между точечным источником света и экраном поместили диафрагму с круглым отвер-стием, радиус которого r можно менять. Расстояния от диафрагмы до источника и эк-рана равны a = 100 см и b = 125 см. Определите длину волны света, если максимум освещенности в центре дифракционной картины на экране наблюдается при r1 = 1 мм, и следующий максимум – при r2 = 1,29 мм. Решение. При решении воспользуемся методом, основанным на построении зон Френеля. Волновую поверхность сферической волны от точечного источника S разобьем на так называемые зоны Френеля - кольцевые зоны, построенные так, что расстояние от точ-ки наблюдения P до внешних границ этих зон увеличивается с шагом λ / 2 , начиная от минимального значения b + (λ / 2) (рис. 1). Можно показать, что при не очень больших номерах зон Френеля их площади практически одинаковы, а радиус m -ой зоны определя-ется выражением
где a и b - расстояния от волновой поверхности до источника S и точки наблюдения P . 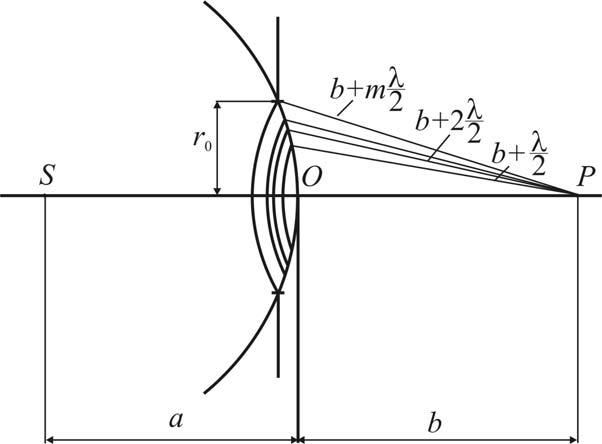 Рис.1 Далее каждую зону Френеля разобьем на очень узкие кольцевые подзоны так, что расстоя-ние от каждой следующей подзоны до точки P увеличивается с постоянным шагом r . Согласно принципу Гюйгенса-Френеля точки волновой поверхности являются ис-точниками вторичных когерентных волн, которые возбуждают колебания в точке наблю-дения P. Колебания в точке P от отдельных кольцевых подзон имеют примерно одинако- вые амплитуды и для соседних подзон сдвинуты по фазе на величину ϕ = 2π r / λ . 1 Просуммируем колебания методом векторных диаграмм, отображая амплитуду ко-лебаний, возбуждаемых в P каждой подзоной, в виде вектора. Фазовый сдвиг учтем, по-ворачивая на угол ϕ каждый следующий вектор относительно предыдущего. Модули векторов слабо уменьшаются с увеличением номера подзоны, что связано со слабым уменьшением площади подзон и с увеличением угла между нормалью к волновой поверх-ности в данной подзоне и направлением на точку P. В результате получим векторную диа-грамму в виде спирали (рис.2), которая называется спиралью Френеля. 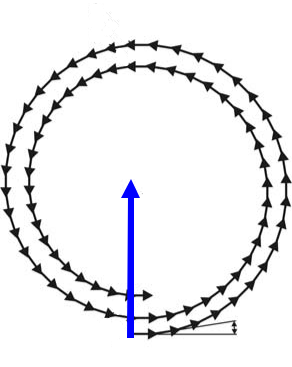 A∞ ϕ Рис.2. Амплитуда результирующих колебаний определяется модулем суммы векторов. По мере увеличения числа подзон результирующий вектор описывает своим концом спираль, которая в случае полностью открытой волновой поверхности сходится к точке F ; при этом амплитуда колебания в точке P равна A∞ . 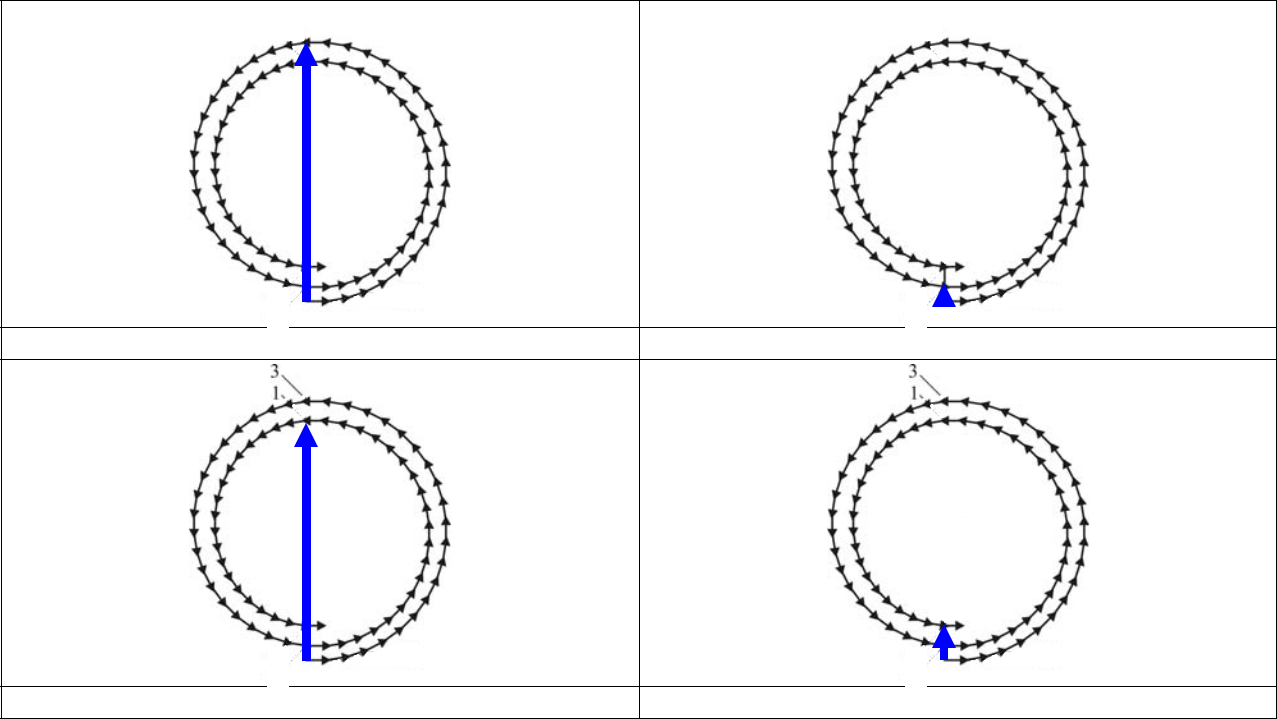
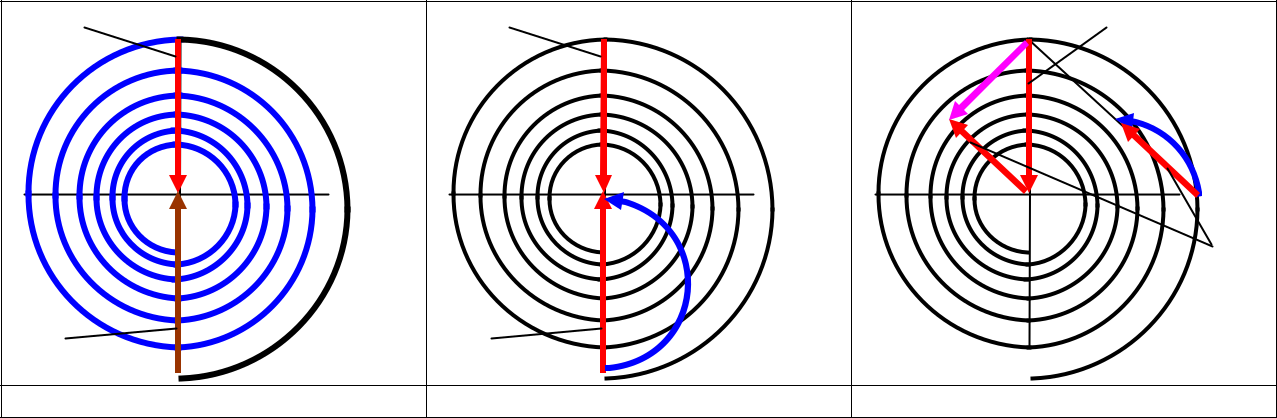
Когда радиус отверстия r0 равен радиусу первой зоны Френеля для точки наблюде- ния P, отверстие открывает вторичные источники, возбуждающие в точке P колебания, последнее из которых сдвинуто по фазе относительно первого на π . Соответствующая векторная диаграмма изображена на рис.3. Видно, что в этом случае амплитуда колебаний точке P в 2 раза, а интенсивность в 4 раза больше, чем в случае, когда открыт весь вол-новой фронт ( r0 → ∞ ). 2 Когда радиус отверстия равен радиусу второй зоны Френеля, колебания вторичных источников первой и второй зон Френеля гасят друг друга (рис.4). При дальнейшем уве-личении радиуса отверстия интенсивность света в точке P будет периодически изменять-ся, достигая максимума, когда открыто нечетное число зон Френеля и минимума, когда открыто четное число зон (рис.5, 6). В данной задаче
где m - целое положительное число. Решая эту систему, найдем = (r22 − r12 )(a + b) = 0,6 мкм. 2ab Пример 2. Плоская монохроматическая световая волна с интенсивностью I0 падает нормально на непрозрачный экран с круглым отверстием. Какова интенсивность света за экраном в точке, для которой отверстие: А) равно первой зоне Френеля, Б) равно внутренней половине первой зоны Френеля, В) сделали равным первой зоне Френеля и затем закрыли его половину (по диаметру)? Решение. А) См. рис.7: A1 = 2A∞ , I1 = 4I∞ , где A∞ и I∞ - амплитуда и интенсивность в точке на-блюдения, когда нет преграды, Б)См.рис.8: A2 = A∞ В) Если закрыть половину отверстия по диаметру, то площадь каждой подзоны умень-шится в 2 раза, поэтому и амплитуда каждого колебания уменьшится в 2 раза при неиз-менном фазовом сдвиге. Следовательно, и векторная диаграмма должна уменьшиться в 2 раза: A3 = A∞ , I3 = I∞ (рис.9). 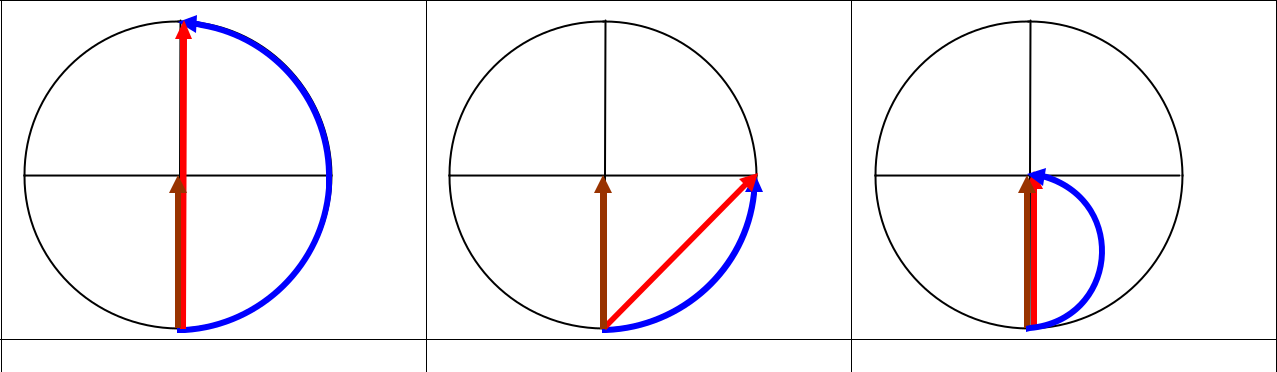
Пример 3. Плоская монохроматическая световая волна с интенсивностью I0 падает нормально на непрозрачный диск, закрывающий для точки наблюдения P первую зону Френеля. 3 Какова стала интенсивность света I в точке P после того, как у диска удалили (по диа-метру): А) половину, Б) половину внешней половины первой зоны Френеля? Решение. А) Показанный на рис. 10 вектор A1 - амплитуда колебаний, возбуждаемых в точке на-блюдения вторичными источниками всех зон Френеля, кроме первой, которая закрыта диском. На рис. 11 показана также амплитуда A2 колебаний, возбуждаемых вторичными
Соответствующая интенсивность равна I∞ / 2 .
 Пример 4. Плоская световая волна с длиной волны λ = 0,6 мкм падает нормально на достаточно большую стеклянную пластинку, на противоположной стороне которой сделана выем-ка (рис. 13). Для точки наблюдения P она представляет собой первые полторы зоны Френеля. Найдите глубину h выемки, при которой интенсивность света в точке P бу-дет максимальной. 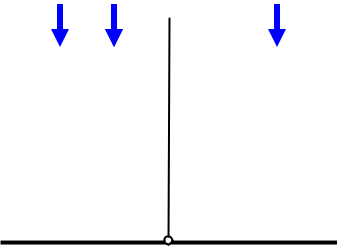 A2 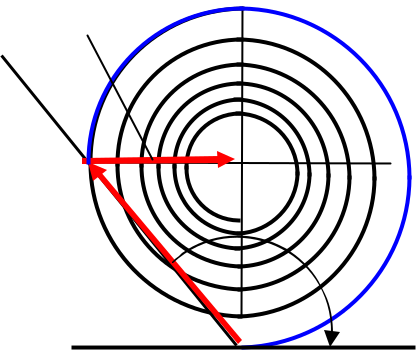
P ϕ
Решение. 4 На рис. 14 вектор A1 отображает колебания, возбуждаемые в точке P вторичными источ-никами, расположенными на целой (без выемки) пластинке в пределах первых полутора зон Френеля, вектор A2 - амплитуда колебаний остальных источников, лежащих на по-верхности целой пластины. «Изготовление» выемки приводит к повороту вектора A1по часовой стрелке на угол = 2λπ (n −1)h , что учитывает отрицательный фазовый сдвиг для волн, распространяю- щихся от дна выемки до точки наблюдения P : ранее эти волны распространялись в стекле толщиной h , а теперь, после изготовления выемки, в воздухе. Из рис. 14 видно, что для получения максимальной интенсивности в точке P угол ϕ должен быть равен = 34 π + 2πm , где m = 0, 1, 2, .. . После преобразований получим ответ
Пример 5. Свет с λ =0,60 мкм падает нормально на поверхность стеклянного диска, который пе-рекрывает полторы зоны Френеля для точки наблюдения P . При какой толщине этого диска интенсивность света в точке P будет максимальной? Решение. Предполагая сначала, что rдиск имеет бесконечно малую толщину, покажем на спирали Френеля (рис. 15) вектор A1,5 , который соответствует суммарному вкладу в амплитуду ре-
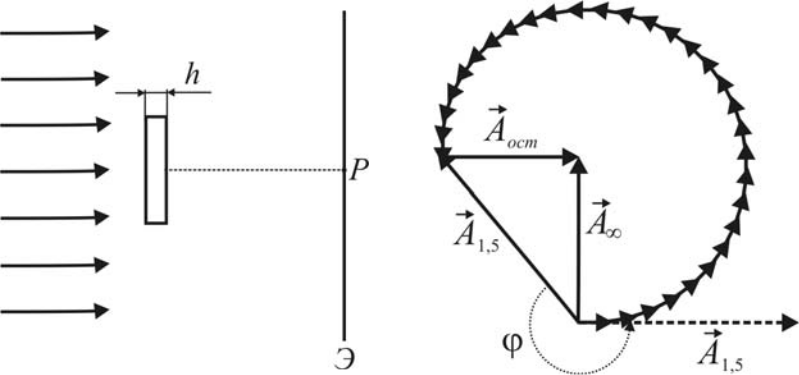 Рис. 15 Если толщина диска становится конечной, падающая волна достигает плоскости, совме-щенной с выходной поверхностью диска, с разными значениями фаз в области диска и вне ее, что обусловлено различиями в скорости распространения света в стекле и в возду-хе. Вследствие этого с ростом толщины диска вторичные волны, испускаемые с его по-верхности, отстают по фазе от значений, соответствующих бесконечно тонкому диску. Величина отставания по фазе связана с толщиной диска h соотношением 5 ϕ = 2λπ (n −1)h , где n - показатель преломления стекла. При построении спирали Френеля отставанию по фазе соответствует поворот элемен-тарного вектора против часовой стрелки. Следовательно, с ростом толщины стеклянного r диска вектор A1,5 поворачивается против часовой стрелки. Интенсивность в точке P будет r максимальна тогда, когда вектор A1,5 будет сонаправлен вектору Aост . Для этого вектор r A1,5должен повернуться на угол = 54 π + 2πm , где m = 0, 1, 2, … После преобразований получим:
6 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
