5 вариант ряды, дифуры. Решение Применим признак Даламбера Согласно признаку Даламбера получим
 Скачать 44.34 Kb. Скачать 44.34 Kb.
|
|
Вариант №5 Задание №1. Исследовать сходимость числового ряда 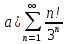 Решение: Применим признак Даламбера: 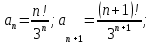 Согласно признаку Даламбера получим: 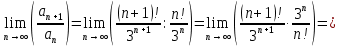 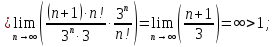 Следовательно, по признаку Даламбера данный ряд расходится. Ответ: ряд расходится. 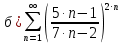 Решение: Применим радикальный признак Коши: 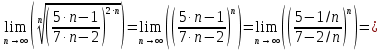 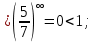 Следовательно, по радикальному признаку Коши данный ряд сходится. Ответ: ряд сходится. 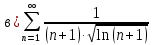 Решение: Применим интегральный признак Коши: 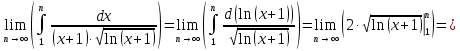 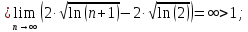 Следовательно, по интегральному признаку Коши данный ряд расходится. Ответ: ряд расходится. Задание №2. Исследовать сходимость знакопеременных рядов. Если ряд сходится, то определить сходится он абсолютно или условно. 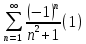 Решение: Рассмотрим ряд: 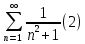 Применим интегральный признак Коши: 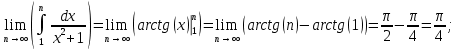 Следовательно, по интегральному признаку Коши данный ряд (2) сходится. А ряд (1) сходится абсолютно. Ответ: ряд сходится абсолютно. Задание №3. Найти область сходимости степенного ряда. 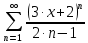 Решение: Находим область сходимости степенного ряда применяя признак Даламбера: 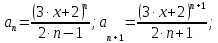 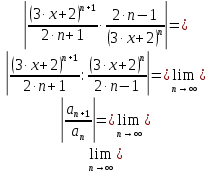 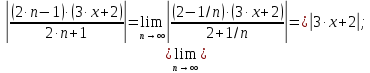 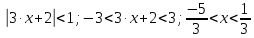 радиус сходимости степенного ряда: R=1; Исследуем ряд на сходимость в концах интервала. а) При x 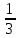 получаем числовой ряд: получаем числовой ряд: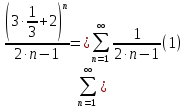 Применим интегральный признак Коши: 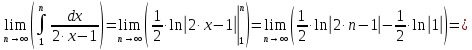 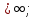 Следовательно, по интегральному признаку Коши данный ряд (1) расходится. Ряд расходится, так как не выполняется необходимое условие сходимости: 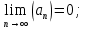 б) При x 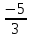 получаем числовой ряд: получаем числовой ряд: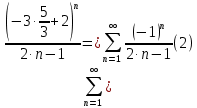 Так как ряд из абсолютных величин (1) расходится, то применим 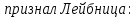 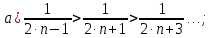 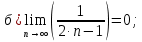 признак 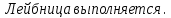 Следовательно ряд (2) сходится, так как не выполняется признак Лейбница и ряд (1) расходится. Следовательно ряд (2) сходится, так как не выполняется признак Лейбница и ряд (1) расходится.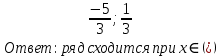 Задание №4. Вычислить определенный интеграл с помощью разложения подынтегральной функции в степенной ряд. Обеспечить абсолютную погрешность h =0,001. 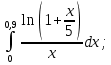 Решение: Из разложения для функции 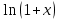 : :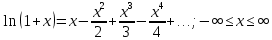 заменяя x на 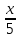 , получаем: , получаем: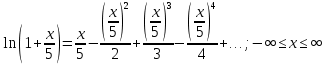 Подставим полученное разложение под знак интеграла: 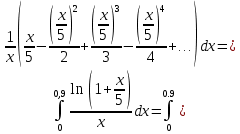 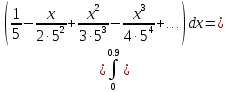 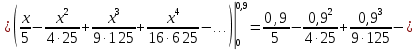 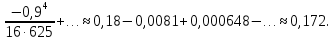 Данный ряд является знакочередующимся, для которого остаток ряда по модулю не превосходит модуль первого члена остатка ряда. Таким образом, вычисления проводятся до тех пор, пока слагаемое по модулю не будет меньше 0,001. 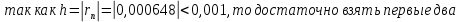 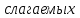 Ответ: 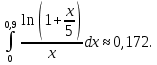 Задание №5. Разложить в ряд Маклорена функцию: 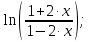 Решение: 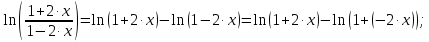 Из разложения для функции 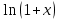 : :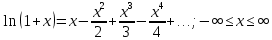 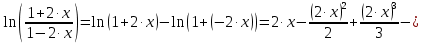 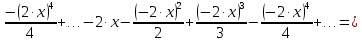 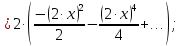 Задание №6. Найти решения дифференциальных уравнений 1-го порядка. 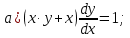 Решение: 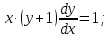 Разделим обе части уравнения на произведение : 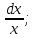 Получим уравнение с разделенными переменными: 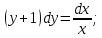 Интегрируя его, найдем: 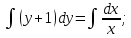 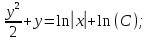 Ответ: 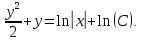 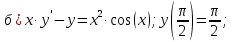 Решение: 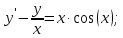 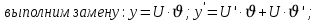 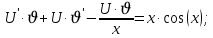 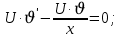 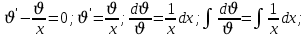 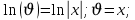 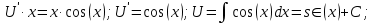 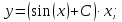 Найдем константу 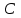 , используя начальное условие , используя начальное условие 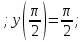 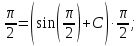 отсюда C=0; Искомое частное решение или решение задачи Коши: 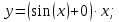 Искомое решение: 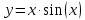 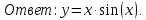 Задание №7. Найти решения дифференциальных уравнений 2-го порядка. 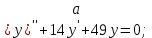 Решение: Составляем характеристическое уравнение: 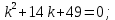 находим корни: 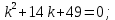 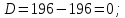 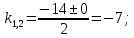 Так как корни уравнения действительные и одинаковые, то решение исходного уравнения имеем в виде: 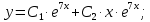 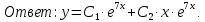 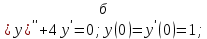 Решение: Составляем характеристическое уравнение: 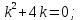 находим корни: 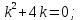  Так как корни уравнения действительные и различны, то решение исходного уравнения имеем в виде: 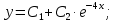 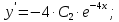 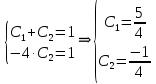 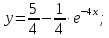 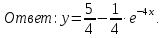 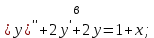 Решение: 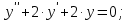 Составляем характеристическое уравнение: 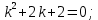 находим корни: 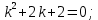 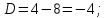 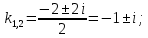  Так как среди корни характеристического уравнения есть комплексные числа, то общее решение: Так как среди корни характеристического уравнения есть комплексные числа, то общее решение: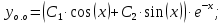 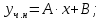 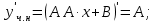 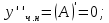 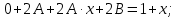 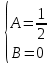 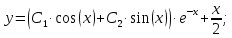 Ответ: 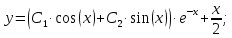 |
