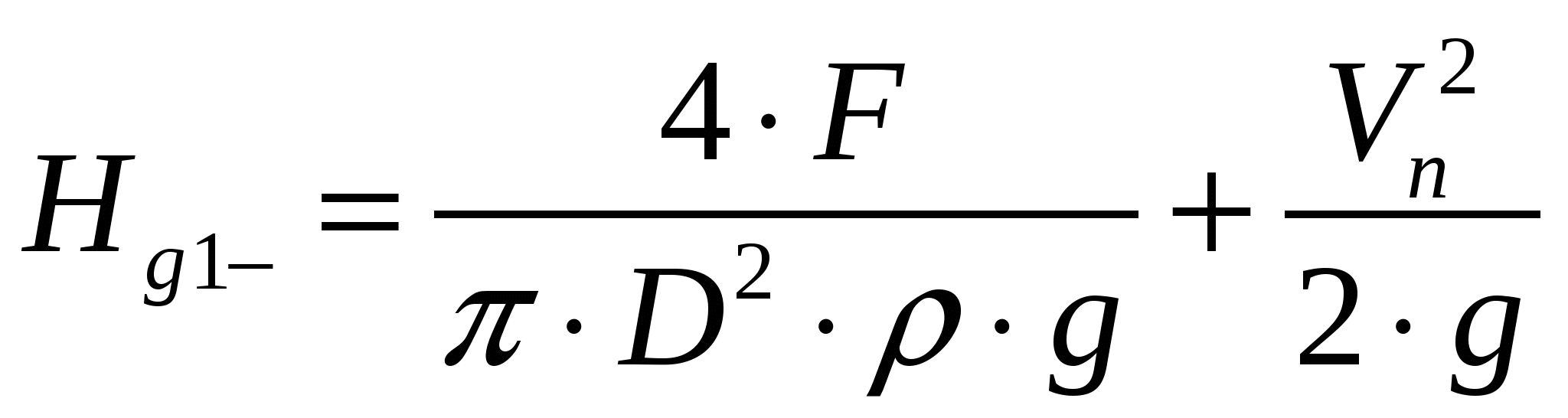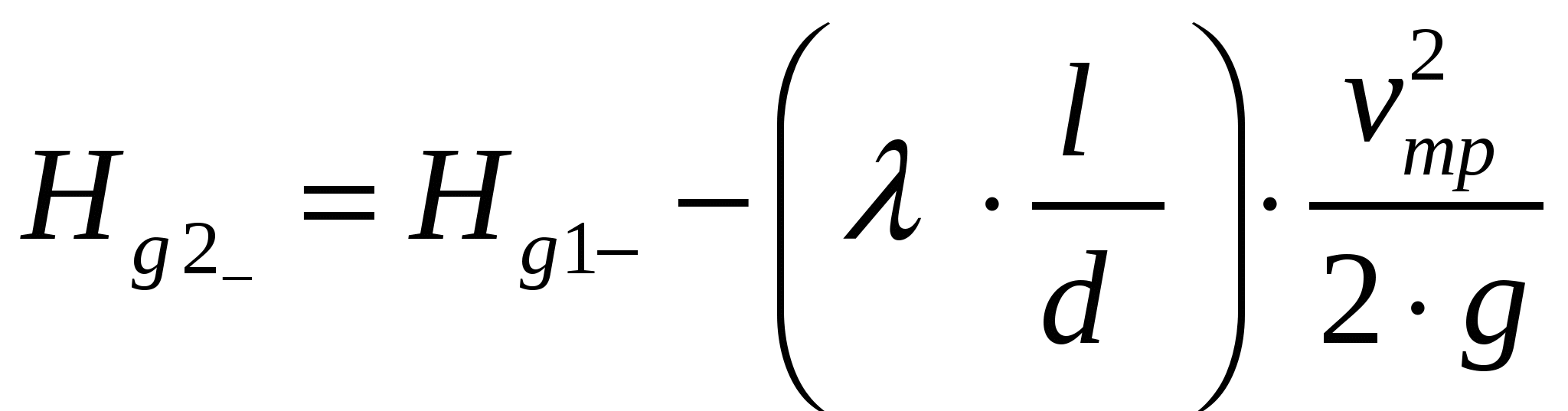Задача 01. Решение Применим уравнение Бернулли для плоскости поршня I и свободной поверхности бака II. Плоскость сравнения проведем через свободную поверхность бака II
 Скачать 188.5 Kb.
|
|
Задача 01 Поршень диаметром D=280мм движется равномерно вниз в цилиндре, подавая жидкостъ воду в открытый резервуар с постоянным уровнем (рис. 1). Диаметр трубопровода d=90мм, его длина l=15м. Когда поршень находится ниже уровня жидкости в резервуаре на Н=5 м потребная для его перемещения сила равна F=19000Н. Определить скорость поршня и расход жидкости в трубопроводе. Построить напорную и пьезометрическую линии для трубопровода. Коэффициент гидравлического трения трубы принять λ=0,03. Коэффициент сопротивления входа в трубу ζвх=0,5. Коэффициент сопротивления выхода в резервуар ζвых=1,0.  Рисунок 1 Решение: Применим уравнение Бернулли для плоскости поршня I и свободной поверхности бака II. Плоскость сравнения проведем через свободную поверхность бака II. 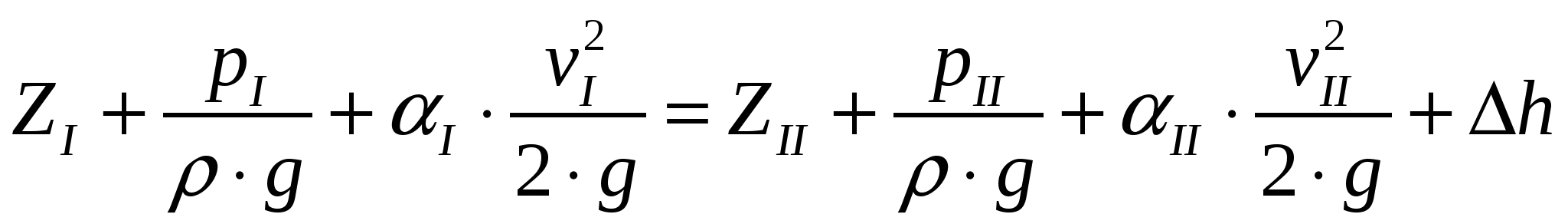 Пологая, что режим течения турбулентный, т. е. 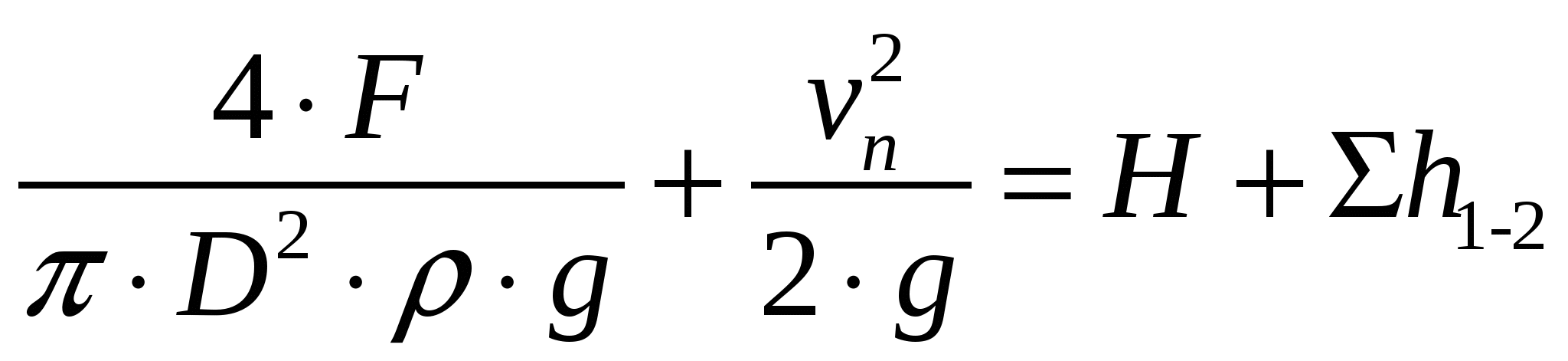 . Учитывая, что большие размеры резервуара и считая скорость изменения уровня свободной поверхности равной нулю  , а также  и  можно записать: В нашем случае получим:  ,Vтр – средняя скорость жидкости по сечению в трубе. где 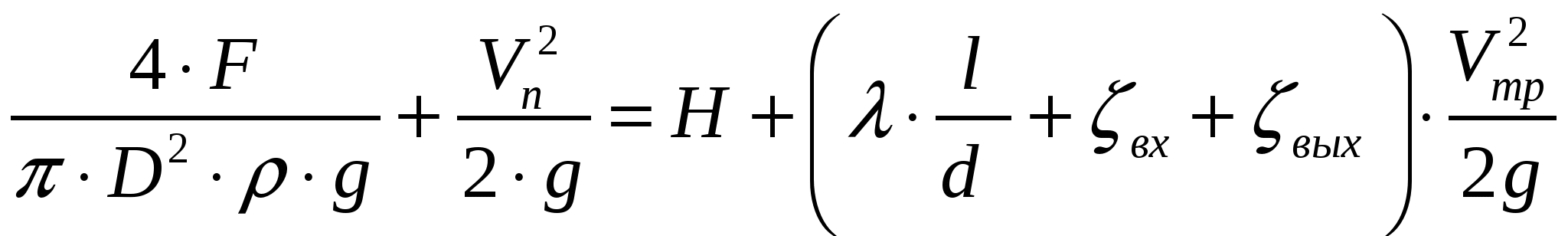 - коэф-т сопротивления входа. - коэф-т сопротивления выхода. Записанное уравнение содержит две неизвестные скорости Vп и Vтр. Выразим скорость V1 через скорость V2. Для этого воспользуемся уравнением неразрывности:      После алгебраических преобразований, уравнение Бернулли принимает окончательный вид:  Полученное уравнение содержит одну неизвестную Vп, которая равна:  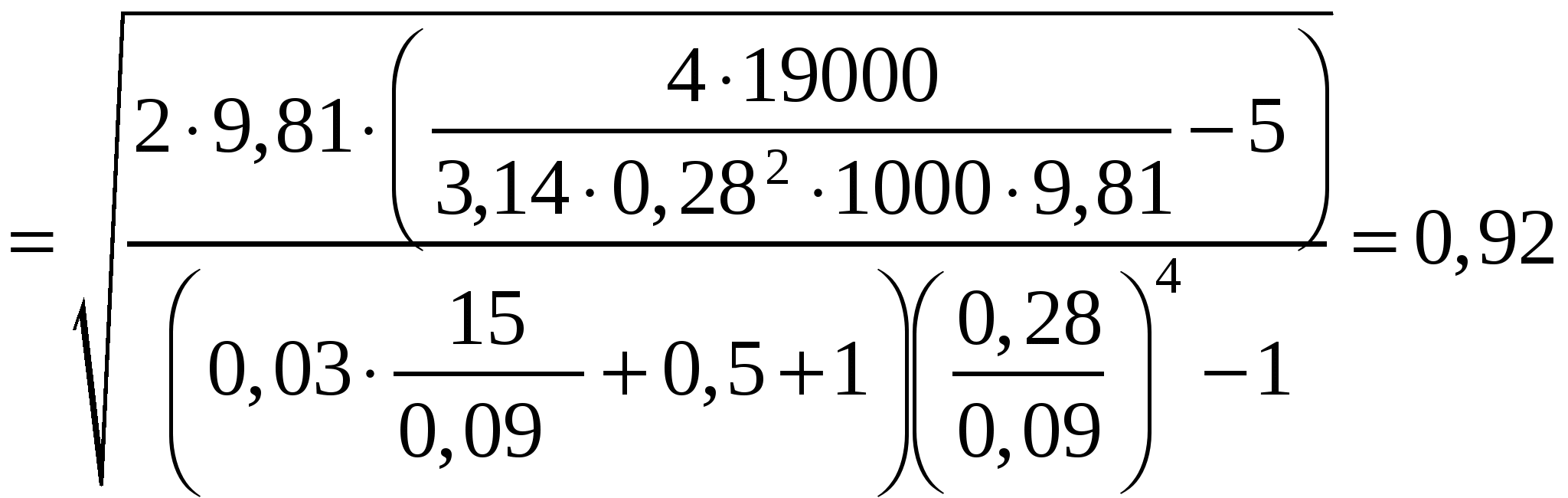 м/с=92см/с кг/м3 – плотность жидкости; м/с2 – ускорение свободного падения.Расход:  м3/с=56,65л/сСтроим график напоров
 |
,м
