Теория вероятностей и математической статистики .. Решение Пусть автомобилей изготовлено второй партией, тогда первой партией изготовлено 3 автомобилей
 Скачать 26.61 Kb. Скачать 26.61 Kb.
|
|
Завод изготовил две партии автомобилей. Первая партия в три раза больше второй. Надежность автомобилей первой партии – 0.9, второй партии – 0.8. Определить вероятность того, что наугад купленный автомобиль будет надежным. Если график функции распределения случайной величины Х имеет вид: 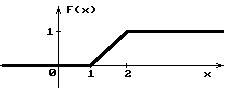 Найти М(X). Решение: Пусть  автомобилей изготовлено второй партией, тогда первой партией изготовлено 3 автомобилей изготовлено второй партией, тогда первой партией изготовлено 3 автомобилей. автомобилей. + 3 + 3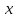 = 1; 4 = 1; 4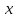 = 1; = 1; 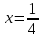 Н1 – автомобиль изготовлен первой партией P(Н1) = 3/4 = 0,75 Н2 – автомобиль изготовлен второй партией Р(Н2) = 1/4 = 0,25 А – купленный автомобиль будет надежным. Условные вероятности этого события равны: Рн 2(А) = 0,9; Рн2(А) = 0,8 По формуле полной вероятности имеем: Р (А) = ∑ P (Нi) ∙ Рнi(А); Р (А) = 0,75 * 0,9 + 0,25 * 0,8 = 0,875 Ответ: 0,875 2. Найдем функцию распределения F ( 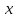 ) . ) .При 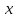 < 1 F ( < 1 F (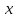 ) = 0 ) = 0 При 1 ≤ 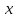 ≤ 2 график проходит через точки (1,0) и (2,1). ≤ 2 график проходит через точки (1,0) и (2,1).Уравнение прямой, проходящее через 2 точки ( 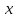 1 ; γ1) и ( 1 ; γ1) и (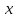 2 ; γ2), имеет вид: 2 ; γ2), имеет вид: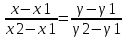 Подставляя в него координаты точек (1,0) и (2,0), получаем: 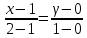 ; ;  ; ; 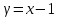 Таким образом, при 1 ≤ 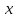 ≤ 2 F( ≤ 2 F(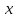 ) = ) = 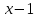 При 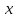 > 2 F ( > 2 F (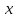 ) = 1 ) = 1Функция распределения примет вид: 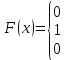  Плотность распределения 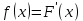 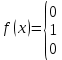  Математическое ожидание: 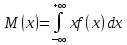 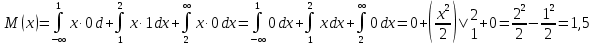 Ответ: 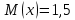 . .Список литературы: Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике: Учеб. пособие для студентов вузов. Изд. 4-е, стер. М.: Высш. шк., 1997. – 400 с.: ил. 2. Гмурман В.Е. Теория вероятностей и математическая статистика. Учеб. пособие для вузов. Изд. 6-е, стер. – М.: Высш. шк., 1997. – 479 с.: ил. 3. Гнеденко Б.В. Курс теории вероятностей: Учебник – Изд. 6-е, перераб. и доп. – М.: Наука. Гл. ред. физ. –мат. лит., 1988. – 448 с. |
