контрольная работа по электротехнике. Решение Расчет методом двух узлов Произвольно указываем направление всех токов в ветвях. R 5 R 2
 Скачать 62.19 Kb. Скачать 62.19 Kb.
|
|
Расчет цепей постоянного тока Дано: E1 =100В, Е2 = 300В R1 = 12Ом, R2 = 24Ом, R3 = 16Ом, R4 = 60Ом, R5 = 50Ом, R6 = 40Ом 1. Предварительно преобразовав пассивный треугольник в эквивалентную звезду, рассчитать токи во всех ветвях схемы методом двух узлов. 2. Рассчитать токи в исходной схеме методом контурных токов. 3. Составить баланс мощностей 4. Построить потенциальную диаграмму для контура, содержащего две ЭДС. Решение: 1.Расчет методом двух узлов Произвольно указываем направление всех токов в ветвях. R5 R2 2      Е2   R6  R3  R4 1 0    3   R1 Е1     1.2 Преобразуем пассивный треугольник сопротивлений в эквивалентную звезду сопротивлений. В данной схеме пассивным является треугольник, содержащий сопротивления R3, R4, R5. 2 2          R56 R6 R5 R46 R45 3 1 2 R4 3 Упрощаем схему. 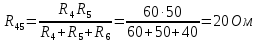   В результате преобразований получаем схему с двумя узлами         Е1 Е2    U00  RⅡ RⅠ RⅢ    Задаем направление токов и напряжения в ветвях преобразованной схемы. Определяем проводимость ветвей    Определяем узловое напряжение, используя метод двух узлов  Определяем токи в ветвях упрощенной схемы по закону Ома для активного участка цепи.    Находим остальные токи в исходной не преобразованной схеме с помощью уравнений второго закона Кирхгофа. 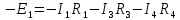 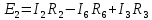 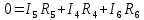 Отсюда 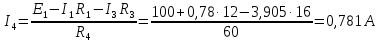   2. Метод контурных токов Выбираем направления контурных токов и положительные направления токов во всех ветвях.         Е1 Е2    Iк1 Iк2    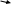 RⅡ RⅠ RⅢ Составляем систему уравнений   Решаем полученную систему с помощью определителей   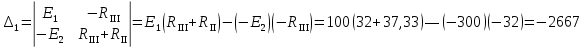 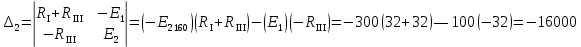 Отсюда     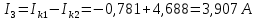 Находим остальные токи в исходной не преобразованной схеме с помощью уравнений второго закона Кирхгофа. 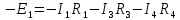 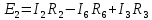 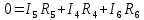 Отсюда    3. Баланс мощностей для заданной электрической цепи По закону сохранения энергии мощность, потребляемая от источника, равна мощности, выделяемой в потребителе.    Погрешность расчета баланса мощностей не превышает 2% 4. Построение потенциальной диаграммы для внешнего контура. Обозначим истинные направления токов в ветвях и зададим направление обхода контура, заземлим любую точку контура и вычислим потенциалы всех других точек.    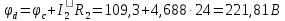   R1 Е1   а b c     Е2    d R5 R2 k Задание №2 Расчет однофазных цепей переменного тока Дано: Е R1 b C1 1 = 100В, R1 = 1Ом, R2 = 3Ом, R3 = 5Ом, С1 = 396Ом, С2 = 796Ом, L3 =12,75мГн   R3 С2 Е  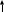  R2 L3 a Задание: 1. Определить токи во всех ветвях схемы и напряжение на каждом элементе цепи: б) символическим методом 2. Составить баланс мощностей. Частота тока f =50Гц. Решение: Найдем величины индуктивных и емкостных сопротивлений    Находим величины реактивных сопротивлений в каждой ветви:  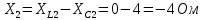 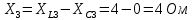 Символический метод расчета цепей синусоидального тока Представляем полные комплексные сопротивления каждой ветви в алгебраической и показательной форме. 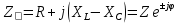 где модуль сопротивления    Эквивалентное сопротивление цепи при смешанном соединении  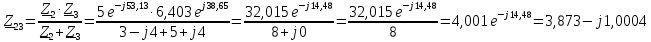 Определяем ток действующий от источника в комплексной форме 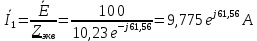 Определим напряжение в комплексной форме в параллельных ветвях:  Определяем комплексные токи в параллельных ветвях   Определяем напряжение комплексное    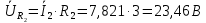    Расчет баланса мощностей Баланс мощностей 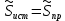 Мощность источника     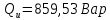     465,48     859,89 Погрешность не превышает 2% Расчет трехфазных сетей Е = 100В, Ra = 1Ом, Rb = 3Ом, Rc = 5Ом, Сa =396Ом, Сb = 354Ом, Сc = 796Ом, La= 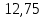 мГн, Lb = мГн, Lb = мГн, Lc = мГн, Lc =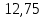 мГн мГнРешение: Найдем величины индуктивных и емкостных сопротивлений  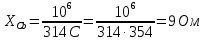     Находим величины реактивных сопротивлений в каждой ветви:  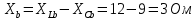 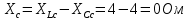 Расчет при соединении в звезду с нулевым проводом Полное сопротивление каждой фазы нагрузки    Система фазных напряжений приемника    По закону Ома в комплексной форме определяется ток в каждой фазе    Определяем ток в нейтральном проводе  Определим полную, активную и реактивную мощность 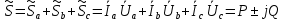   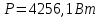 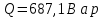 Расчет при соединении в звезду без нулевого провода Определяем напряжение смещения нейтрали  Комплексы полной проводимости фаз     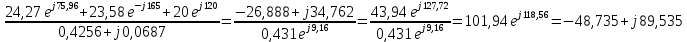 Определяем напряжения и токи в фазах нагрузки  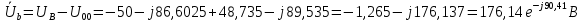  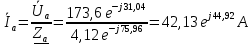   Определим полную, активную и реактивную мощность 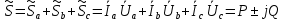  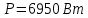  Расчет цепи при соединении в треугольник Находим фазные и линейные напряжения 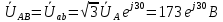  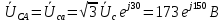 Определяем фазные токи  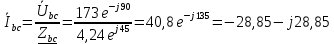 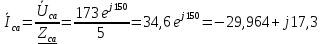 Определяем линейные токи    Проверка   Определяем полную, активную и реактивную мощности    |
