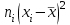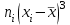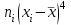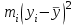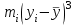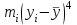статистика. ККМ5. Решение Расположим по убыванию (проранжируем) каждую выборку. Результаты представим в таблице Размах вариации
 Скачать 68.75 Kb. Скачать 68.75 Kb.
|
|
При определении степени выраженности некоторого психического свойства в двух группах, опытной и контрольной, баллы распределились следующим образом: Опытная группа - 19, 16, 17, 12, 15,16. 17,17, 21, 23, 18, 13, 12, 13, 19, 20. 21 Контрольная - 27, 9, 12, 13,26, 23, 14, 15,22,21, 16, 16, 18, 17, 10, 12, 17 Дать сравнительную характеристику степени выраженности этого свойства в данных группах. Решение: 1. Расположим по убыванию (проранжируем) каждую выборку. Результаты представим в таблице:  Размах вариации: R = xmax – xmin Опытная группа: R = 23 – 12 = 11. Контрольная группа: R = 27 – 9 = 18. Для каждой выборки подсчитаем частоту встречаемости различных значений баллов и составим ряд распределения. Для нахождения требуемых характеристик составим расчетные таблицы: Опытная группа
Контрольная группа
Выборочные средние (соответственно для опытной и контрольной групп) равны: 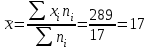 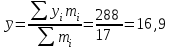 Мода (Mo) ‒ варианта, встречающаяся в изучаемой совокупности чаще всего, т.е. варианта, которой соответствует наибольшая частота. Для дискретного ряда распределения мода определяется наиболее просто: варианта, против которой располагается наибольшая частота, и будет модой. В нашем случае имеем: Опытная группа – Mo=17. Контрольная группа – Мода отсутствует (имеются несколько показателей с одинаковым значением). Медиана (Mе) ‒ варианта, находящаяся в средине ряда распределения. Для ее определения достаточно расположить в порядке возрастания или убывания все варианты. Срединная варианта и будет являться медианой. В нашем случае имеем: Опытная группа - Mе =17. Контрольная группа - Mе =17. Вывод: Размах вариации баллов в контрольной группе выше, чем в опытной. Средний балл в контрольной группе ниже, чем в опытной. В опытной группе имеем симметричный ряд Mo = Me = 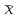 . В контрольной группе Me > . В контрольной группе Me > 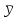 и имеем левостороннюю асимметрию. и имеем левостороннюю асимметрию.Выборочные дисперсии (соответственно для опытной и контрольной групп) равны: 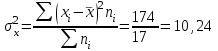 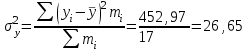 Выборочное среднеквадратическое отклонение (стандартное отклонение) найдем по формуле: 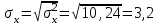 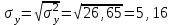 Коэффициент вариации: 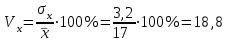 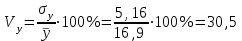 Для нахождения выборочных коэффициентов асимметрии и эксцесса воспользуемся формулами: 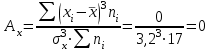 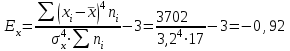 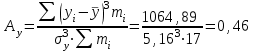 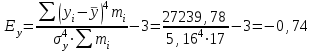 Коэффициент асимметрии характеризует скошенность распределения по отношению к математическому ожиданию. Коэффициент эксцесса характеризует островершинность распределения по отношению к нормальному. Близость к нулю значений коэффициентов асимметрии и эксцесса свидетельствует о нормальном законе распределения. Вывод: Стандартное отклонение в обоих случаях имеет значение существенно меньшее среднего значения. Коэффициенты вариации менее 33%. Таким образом, обе выборки однородны, а полученные средние значения типичны. Близость к нулю значений коэффициентов асимметрии и эксцесса свидетельствует о том, что распределение баллов в опытной и контрольной группах близко к нормальному закону распределения. Сравним степень выраженности этого психического свойства в данных группах. Мы получили, что среднее значение баллов в контрольной группе выше, чем в опытной. Проверим, насколько значимо полученное различие. Для проверки гипотезы 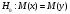 (равенства математических ожиданий) при альтернативной (равенства математических ожиданий) при альтернативной 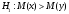 воспользуемся t-критерием Стьюдента. В предположении, что гипотеза воспользуемся t-критерием Стьюдента. В предположении, что гипотеза 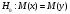 верна, величина верна, величина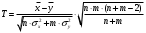 удовлетворяет t-распределению Стьюдента с 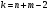 степенями свободы. степенями свободы.В нашем случае имеем: 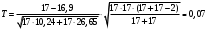 По таблице критических точек распределения Стьюдента при уровне значимости =0,05 и k =32 степенях свободы находим: 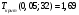 . Так как . Так как 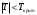 , то гипотеза равенства математических ожиданий в соответствии с критерием Стьюдента при уровне значимости =0,05 принимается. , то гипотеза равенства математических ожиданий в соответствии с критерием Стьюдента при уровне значимости =0,05 принимается.Вывод: Различие степени выраженности некоторого психического свойства в опытной и контрольной группах статистически незначимо. |