Сложное движение точки. сложное движение 14.. Решение. Рассматриваем движение точки
 Скачать 132.64 Kb. Скачать 132.64 Kb.
|
|
R=3 м, 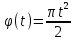 рад рад 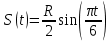 м, t =0,5 c м, t =0,5 cРешение.  Рассматриваем движение точки М как сложное, считая ее движение по желобу относительным, а вращение дуги радиуса R– переносным. Тогда абсолютная скорость и абсолютное ускорение точки найдутся по формулам: 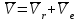  или в развернутом виде или в развернутом виде 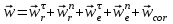 Положение т.М приt=0,5 c 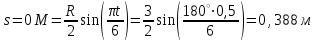 Направление движение точки М – в сторону положительных значений. Угол 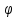 в момент времениt равен: в момент времениt равен: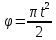 рад=0,393 рад рад=0,393 рад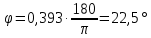 Расстояние  Относительное движение. Относительная скорость 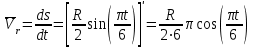 при  c c  Вектор 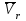 направлен в сторону положительных значений направлен в сторону положительных значений 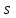 . .Модуль относительного касательного ускорения  , , где 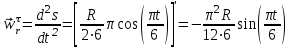 при  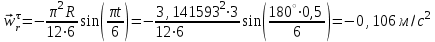 Относительное движение т.М равнозамедленное.  Относительное нормальное ускорение 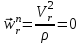 так как траектория относительного движения – прямая линия (  ). ).Переносное движение. Модуль переносной скорости  , , где R1=O1M- радиус окружности , описываемой той точкой тела, с которой совпадает в данный момент т.М.  – модуль угловой скорости тела: – модуль угловой скорости тела: 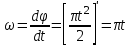 При  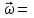 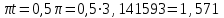 с-1 с-1Модуль переносной скорости:  Вектор 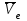 направлен по касательной к окружности радиуса R1 в сторону вращения тела. направлен по касательной к окружности радиуса R1 в сторону вращения тела.Модуль переносного вращательного ускорения  , , где 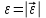 - модуль углового ускорения тела: - модуль углового ускорения тела: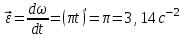 При 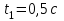  то есть переносное вращательное движение равноускоренное. 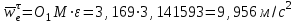 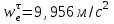 Модуль переносного центростремительного ускорения  Вектор 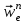 направлен от т .M к т. O1. направлен от т .M к т. O1.Кориолисово ускорение  Модуль кориолисова ускорения 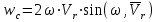 , , где 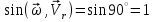  Вектор 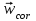 направлен в соответствии с правилом векторного произведения. направлен в соответствии с правилом векторного произведения.Абсолютная скорость. Абсолютную скорость т.М найдем как геометрическую сумму относительной и переносной скоростей.  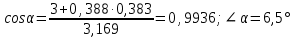 Из геометрических построений: угол между векторами 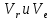 равен равен  Модуль абсолютной скорости определим как 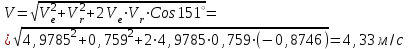  Абсолютное ускорение: Модуль абсолютного ускорения находим методом проекций: 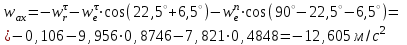 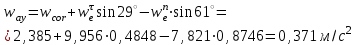  =12,611 м/с2 =12,611 м/с2Ответ: 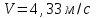 w=12,611 м/с2
|
