ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ -3 исправ. Решение. Рассмотрим участок ав. Составляем дифференциальные уравнения движения тела на участке ав m m g
 Скачать 117.39 Kb. Скачать 117.39 Kb.
|
|
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ. Вариант 3. 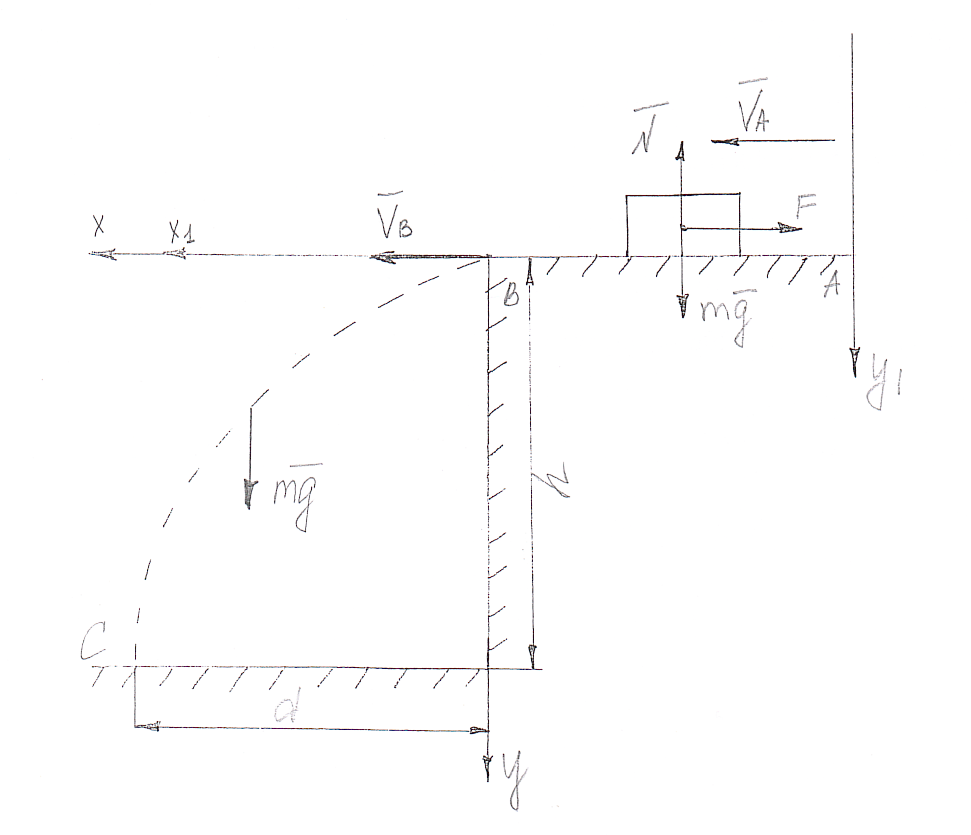 Рисунок 1.1 Имея в точке А скорость 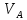 , тело движется по горизонтальному участку АВ , тело движется по горизонтальному участку АВ (длиной l) в течение τ секунд. Коэффициент трения скольжения тела по плоскости равен f. Со скоростью 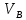 тело в точке В покидает плоскость и попадает в точку С со скоростью тело в точке В покидает плоскость и попадает в точку С со скоростью 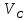 , находясь в воздухе Тсекунд. При решении задачи принять тело за материальную точку. Сопротивление воздуха не учитывать. , находясь в воздухе Тсекунд. При решении задачи принять тело за материальную точку. Сопротивление воздуха не учитывать.Дано: 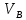 =3м/c, =3м/c, =0.3, =0.3,  =3м, h=5м. =3м, h=5м.Определить: 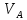 , T-? , T-?Решение. Рассмотрим участок АВ. Составляем дифференциальные уравнения движения тела на участке АВ: m  =- =-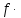 m m g; g;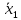 =- =-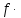 g; g;Интегрируем два раза: 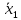 =- =-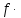 g g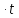 + +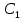 ; ; =-0.5 =-0.5 g g + +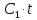 + +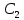 ; ;Константы интегрирования находим по начальным условиям: При 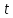 =0, =0, 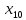 =0, =0,  = =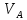 : :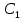 = =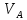 ; ;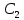 =0; =0;Получаем: 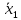 =- =-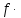 g g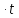 + +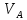 ; ;  =-0.5 =-0.5 g g + +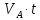 ; ; При 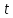 =τ, =τ,  = = =3м, =3м, 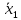 = =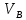 =3м/c, g =3м/c, g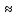 9.81м/ 9.81м/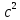 , ,  =0.3: =0.3:3=-2.943  τ+ τ+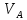 ; (1) ; (1)3=-1.4715  + +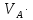 τ; (2) τ; (2) Из (1): τ=( 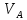 -3)/2.943 -3)/2.943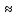 0.34 0.34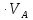 -1.02; -1.02;Из (2): 1.4715  - -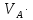 τ+3=0; τ+3=0;1.4715 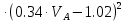 - -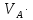 (0.34 (0.34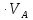 -1.02)+3=0; -1.02)+3=0;1.4715  (0.1156 (0.1156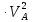 -0.6936 -0.6936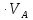 +1.0404)-0.34 +1.0404)-0.34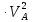 +1.02 +1.02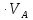 +3=0; +3=0;0.17 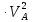 -1.02 -1.02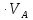 +1.53-0.34 +1.53-0.34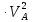 +1.02 +1.02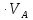 +3=0; +3=0;-0.17 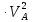 +4.53=0; +4.53=0; =4.53/0.17 =4.53/0.17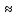 26.65; 26.65;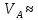 5.16м/c; 5.16м/c;Рассмотрим участок ВС. Составляем дифференциальные уравнения движения: m 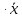 =0; =0; =0; =0;m  =m =m g; g;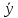 =g; =g;Интегрируем два раза:  = =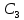 ; ;x= 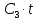 + +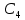 ; ;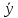 =g =g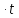 + +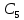 ; ;y=0.5  g g + +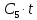 + + ; ;При начальных условиях: 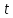 =0, =0, 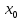 = =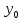 =0, =0, 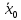 = =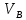 =3м/c, =3м/c, 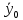 =0: =0: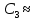 3; 3;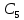 = =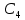 = = =0; =0;При 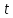 =T, x=d, y=h=5м: =T, x=d, y=h=5м:d=3  T; (3) T; (3)5=0.5  9.81 9.81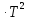 ; (4) ; (4)Из (4): 4.905 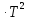 =5; =5;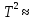 1.0193679; 1.0193679;T 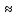 1.01c; 1.01c; Ответ: 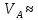 5.16м/c, T 5.16м/c, T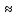 1.01c. 1.01c. |
