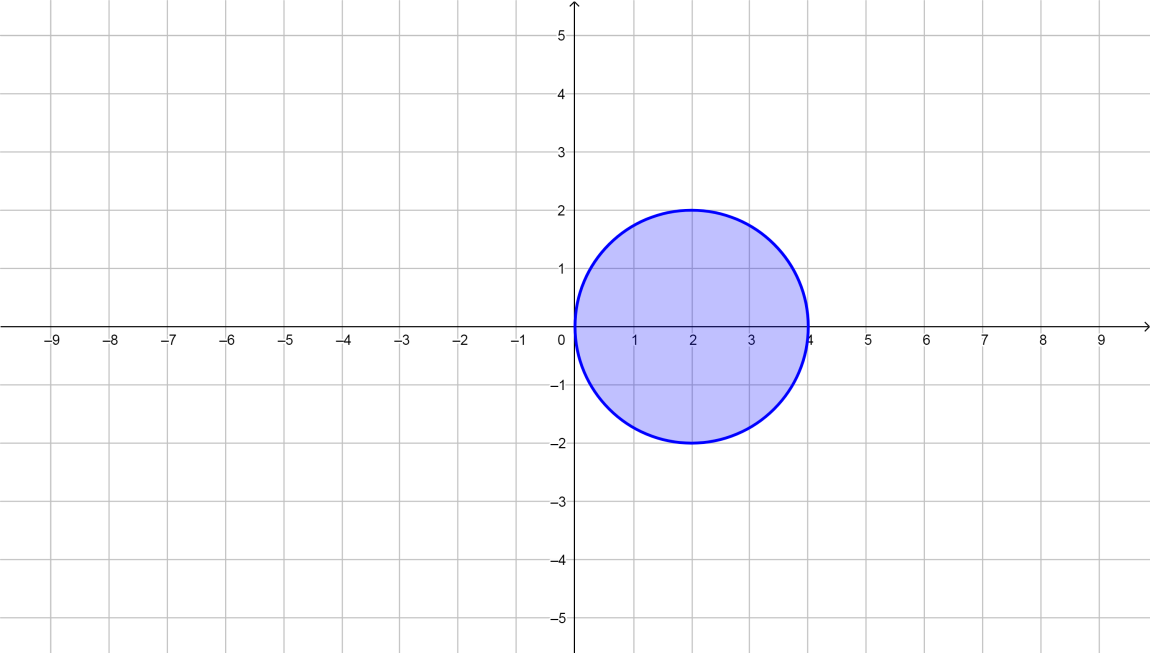
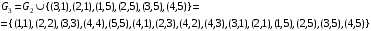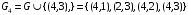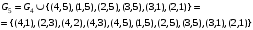Контрольная работа. Решение Решение Найдем множество корней уравнения Методом подбора получаем Тогда Откуда
 Скачать 3.05 Mb. Скачать 3.05 Mb.
|
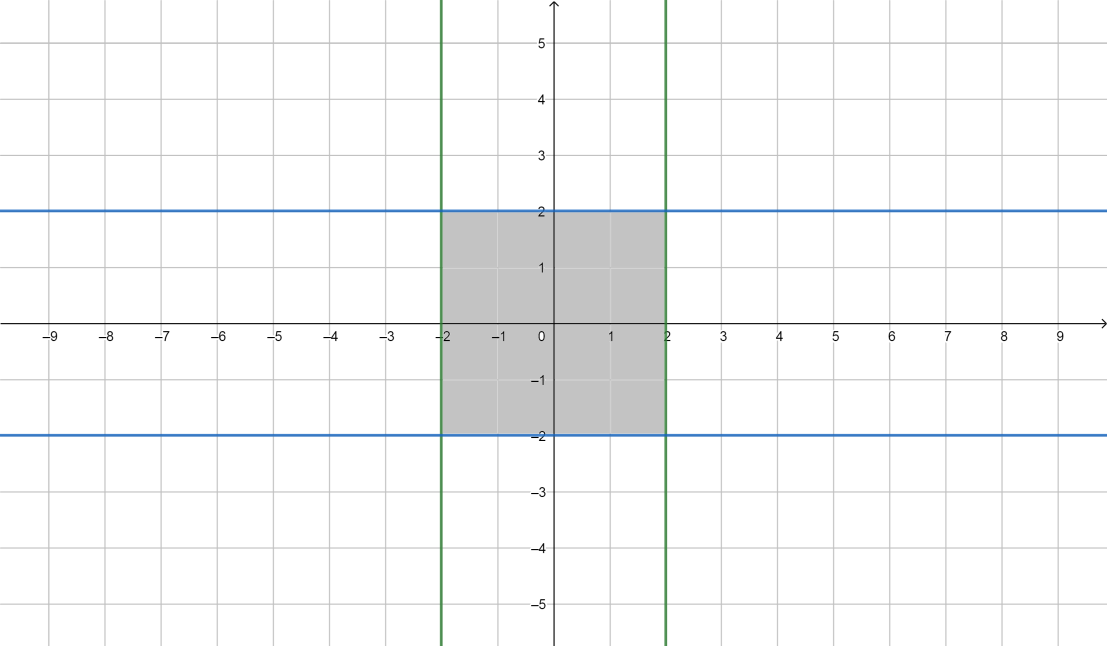
   Контрольные работы по дисциплине «Дискретная математика» для студентов ИИФО специальностей 09.03.01 и 11.03.02 Стр5из19 КОНТРОЛЬНАЯ РАБОТА ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ Основные понятия теории множеств. Способы задания множеств. Операции над множествами 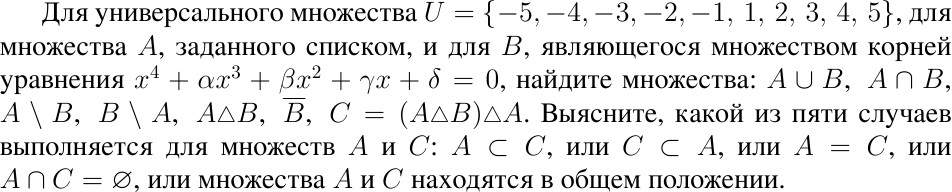 ЗАДАНИЕ 1.1. ЗАДАНИЕ 1.1.Решение: Решение: Найдем множество корней уравнения 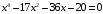 Методом подбора получаем 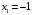 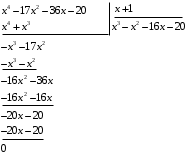 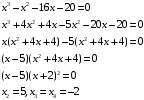 Тогда 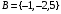 Откуда 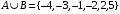 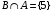 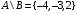 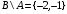 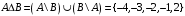 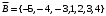 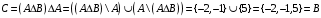 Поскольку 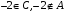 и и 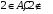 и и 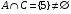 , то имеем множества общего положения. , то имеем множества общего положения.Диаграммы Эйлера-Венна ЗАДАНИЕ 1.2Используя диаграммы Эйлера – Венна, опишите множество, соответствующее части диаграммы, закрашенной серым цветом. 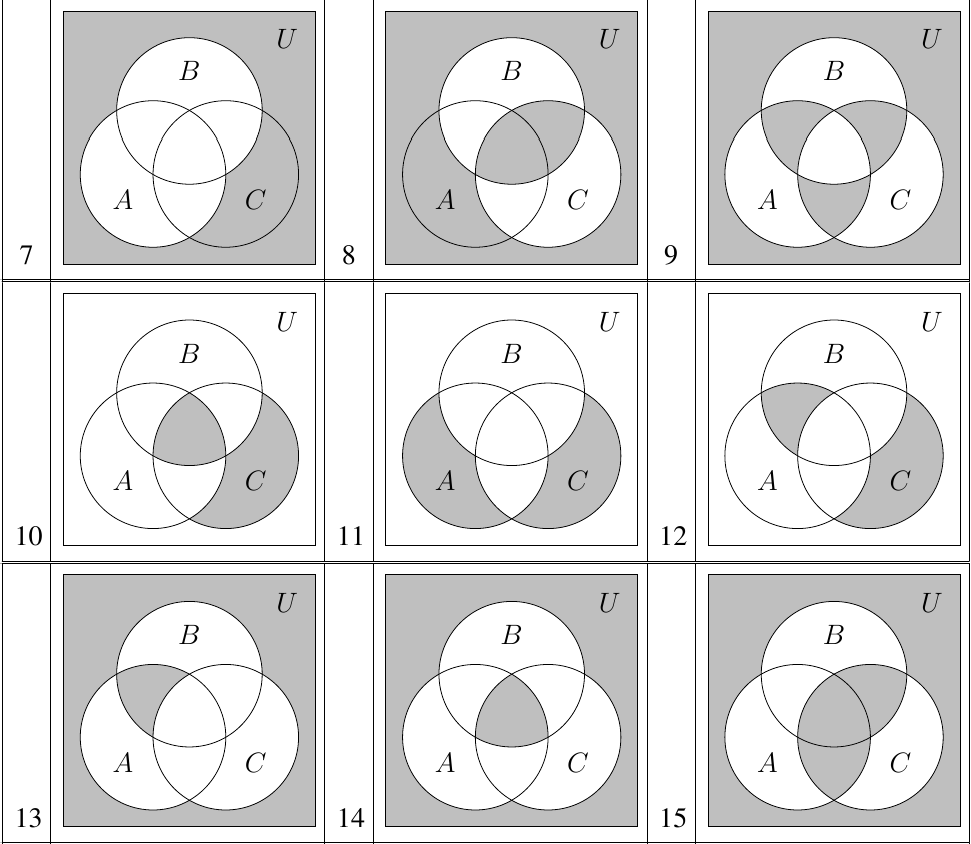 Решение: Имеем множество тех элементов, которые не принадлежат ни множеству А, ни множеству В, но принадлежат множеству С и универсальному множеству. Таким образом, имеем объединение множеств 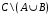 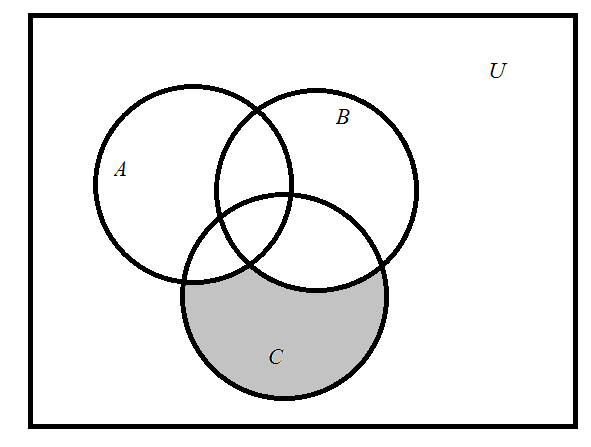 И 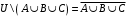 : :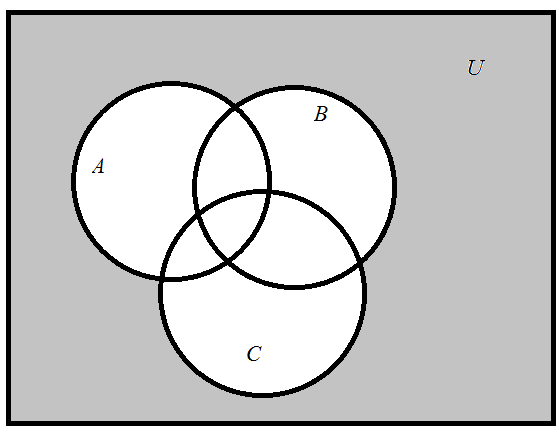 Тогда данное множество имеет вид 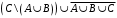 Ответ: 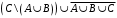
|
 | 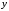 |  | 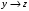 | 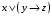 |
| 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
Построим таблицу истинности для второй формулы:
 | 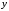 |  | 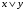 | 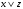 | 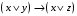 |
| 0 | 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 |
Поскольку при одинаковых наборах переменных формулы принимают одинаковые значения, то они эквивалентны.
Определим, является ли переменная
 существенной или фиктивной.
существенной или фиктивной. Поскольку
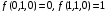 , то
, то  – существенная переменная.
– существенная переменная.Поскольку
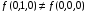 , то переменная
, то переменная 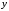 является существенной.
является существенной.Поскольку
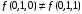 , то переменная
, то переменная  является существенной. Таким образом, фиктивных переменных функция не имеет.
является существенной. Таким образом, фиктивных переменных функция не имеет.Представление булевых функций разложением по переменным
ЗАДАНИЕ 2.2
Для булевой функции, заданной вектором значений, определить:
СДНФ,
СКНФ,
 полином Жегалкина.
полином Жегалкина.Решение:
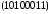
Решение:
Построим таблицу истинности для данной функции
 | 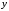 |  | 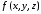 |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
Для построения СДНФ для каждого набора переменных, при котором функция равна 1, записываем произведение, причем переменные, которые имеют значение 0, возьмем с отрицанием.
Получим СДНФ:
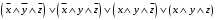
Для построения СКНФ для каждого набора переменных, при котором функция равна 0, записываем сумму, причем переменные, которые имеют значение 1, возьмем с отрицанием.
Получим СКНФ:
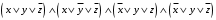
Построим полином Жегалкина при помощи метода неопределенных коэффициентов.
Будем искать полном в виде:
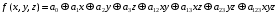
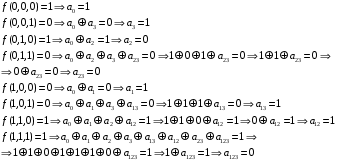
Тогда
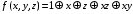 – полином Жегалкина данной функции.
– полином Жегалкина данной функции.ЭЛЕМЕНТЫ ТЕОРИИ ГРАФОВ. ОПТИМИЗАЦИЯ НА ГРАФАХ
Основные понятия теории графов
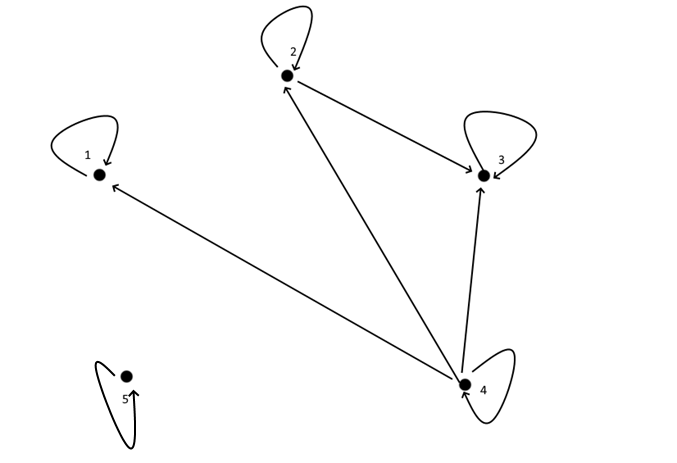
ЗАДАНИЕ 3.1
В таблице для каждого варианта заданы декартовы координаты вершин графа и перечислены ребра графа. Граф неориентирован. Следует построить граф на плос- кости xOyи найти:
таблицу степеней вершин;
матрицу смежности;
матрицу инцидентности;
таблицу расстояний в графе;
 определить радиус и центр графа.
определить радиус и центр графа.Решение:
Построим данный граф:
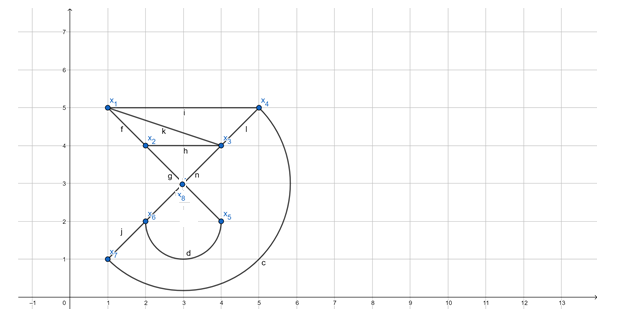
Построим таблицу степеней вершин:
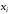 | 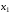 | 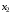 | 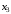 | 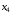 | 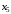 | 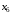 | 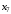 | 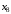 |
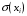 | 3 | 3 | 4 | 3 | 2 | 3 | 2 | 0 |
Построим матрицу смежности для данного графа:
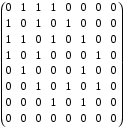
Построим матрицу инцидентности для данного графа. Строки будут отвечать вершинам, столбцы – ребрам. Получим:
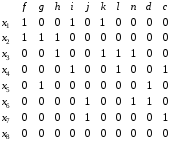
| |  |  |  | 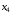 | 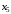 | 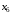 | 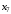 | 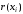 |
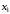 | 0 | 1 | 1 | 1 | 2 | 3 | 2 | 3 |
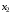 | 1 | 0 | 1 | 2 | 1 | 2 | 3 | 3 |
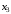 | 1 | 1 | 0 | 1 | 2 | 1 | 2 | 2 |
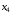 | 1 | 2 | 1 | 0 | 3 | 2 | 1 | 3 |
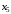 | 2 | 1 | 2 | 3 | 0 | 1 | 2 | 3 |
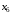 | 3 | 2 | 1 | 2 | 1 | 0 | 1 | 3 |
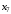 | 2 | 3 | 2 | 1 | 2 | 1 | 0 | 3 |
Тогда радиус графа равен
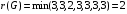
Тогда центр графа составляют множество вершины
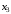
Задачи оптимизации на графах
ЗАДАНИЕ 3.2
Для графа, описанного в задании 3.1 вычислить:
Минимальное остовное дерево.
Кратчайший путь из одного источника.
Для решения задач данного раздела считать граф ориентированным (направле- ние дуги отмечается упорядоченной парой вершин, формирующих ребро). Вес дуги равен длине отрезка между вершинами графа.
Решение:
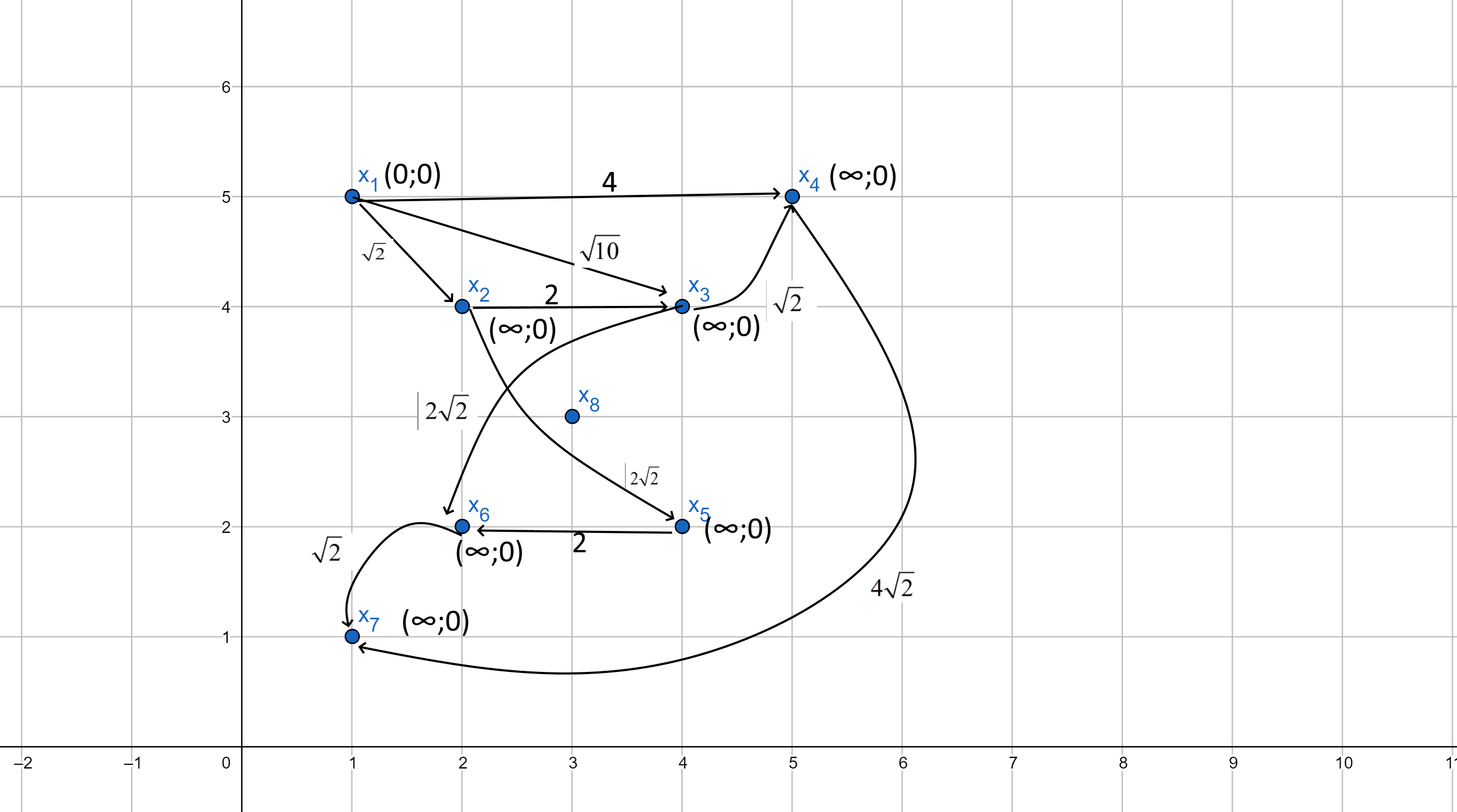
Изобразим данный нагруженный граф:
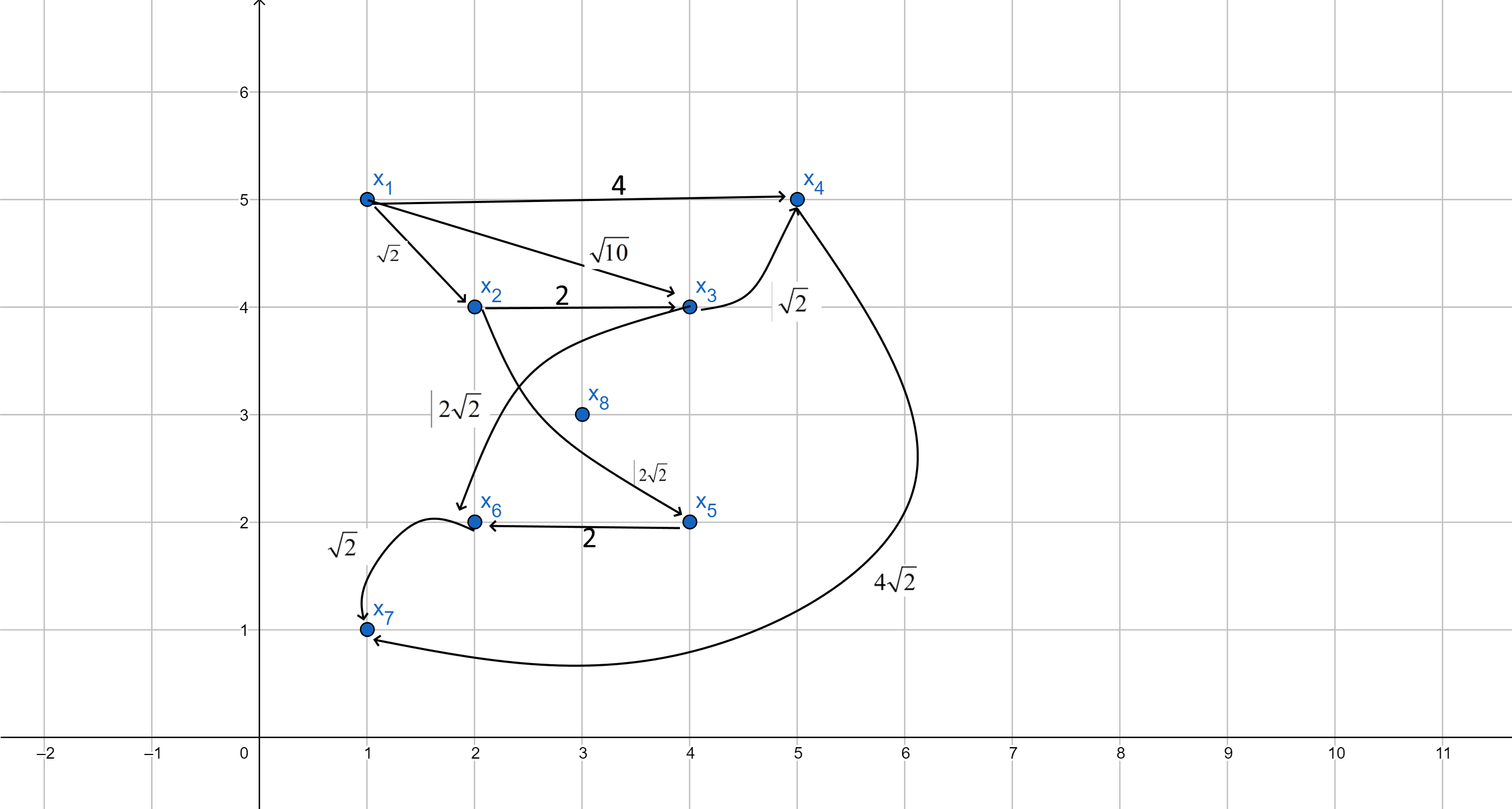
Построим остовное дерево минимального веса. Построение начнем с ребра с минимальным весом
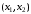 . Порядок присоединения ребер к остову:
. Порядок присоединения ребер к остову: 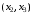 ,
, 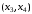 ,
, 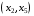 ,
, 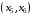 ,
, 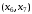 :
: 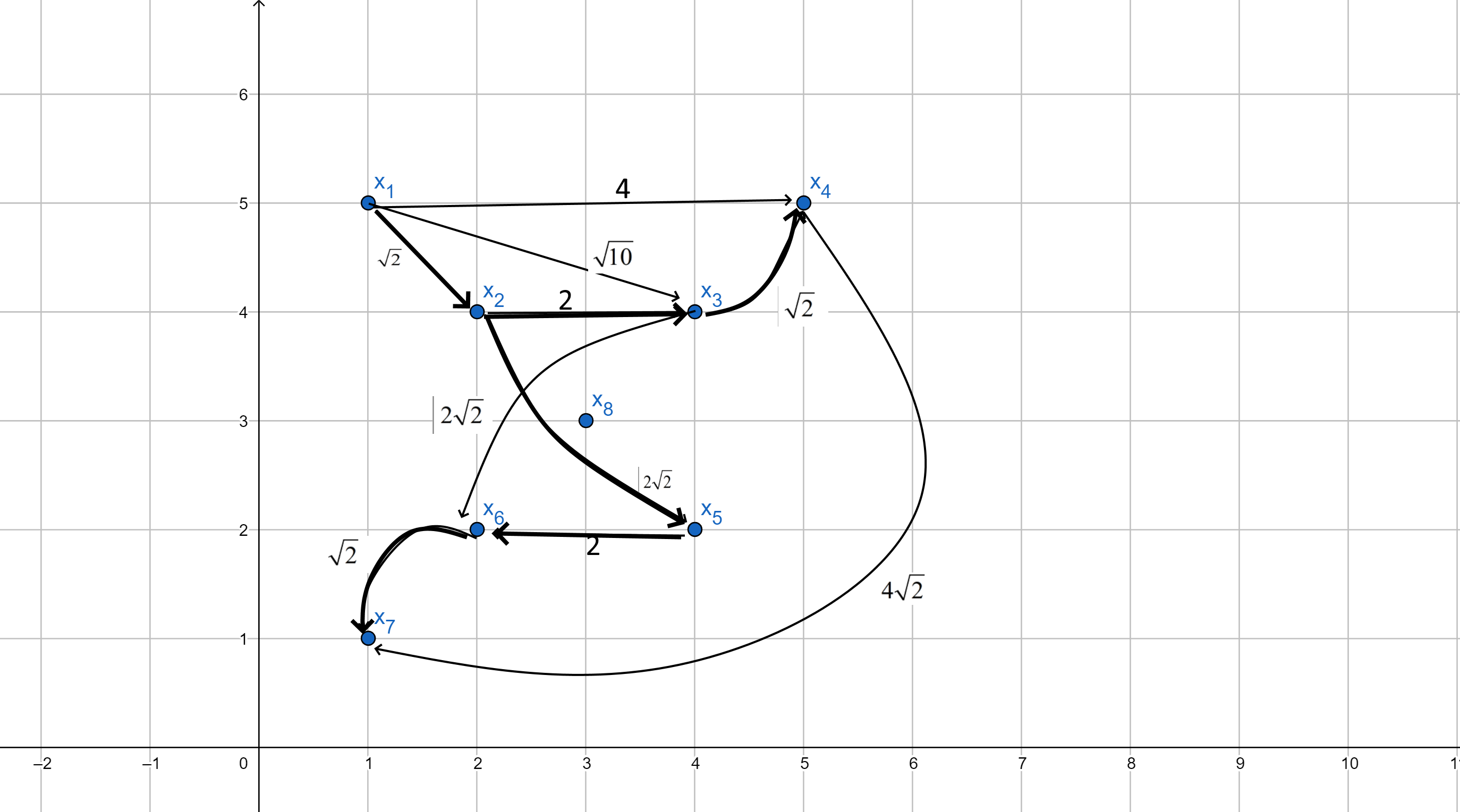
Вес остова равен
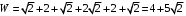
Найдем кратчайший путь из вершины
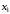 до вершин
до вершин 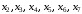 :
:Вершины снабжаем пометками, и в графе будут присутствовать метки
 , пока не найден путь.
, пока не найден путь.Вершины, которые будут становиться постоянными, выделяем знаком *.
Вершина
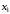 стала постоянной. Метки смежных вершин меняем соответственно на (4, х1), (
стала постоянной. Метки смежных вершин меняем соответственно на (4, х1), (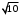 , х1), (
, х1), (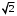 , х1):
, х1):Минимальное из расстояний
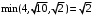 , поэтому вершина
, поэтому вершина 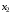 становится постоянной.
становится постоянной.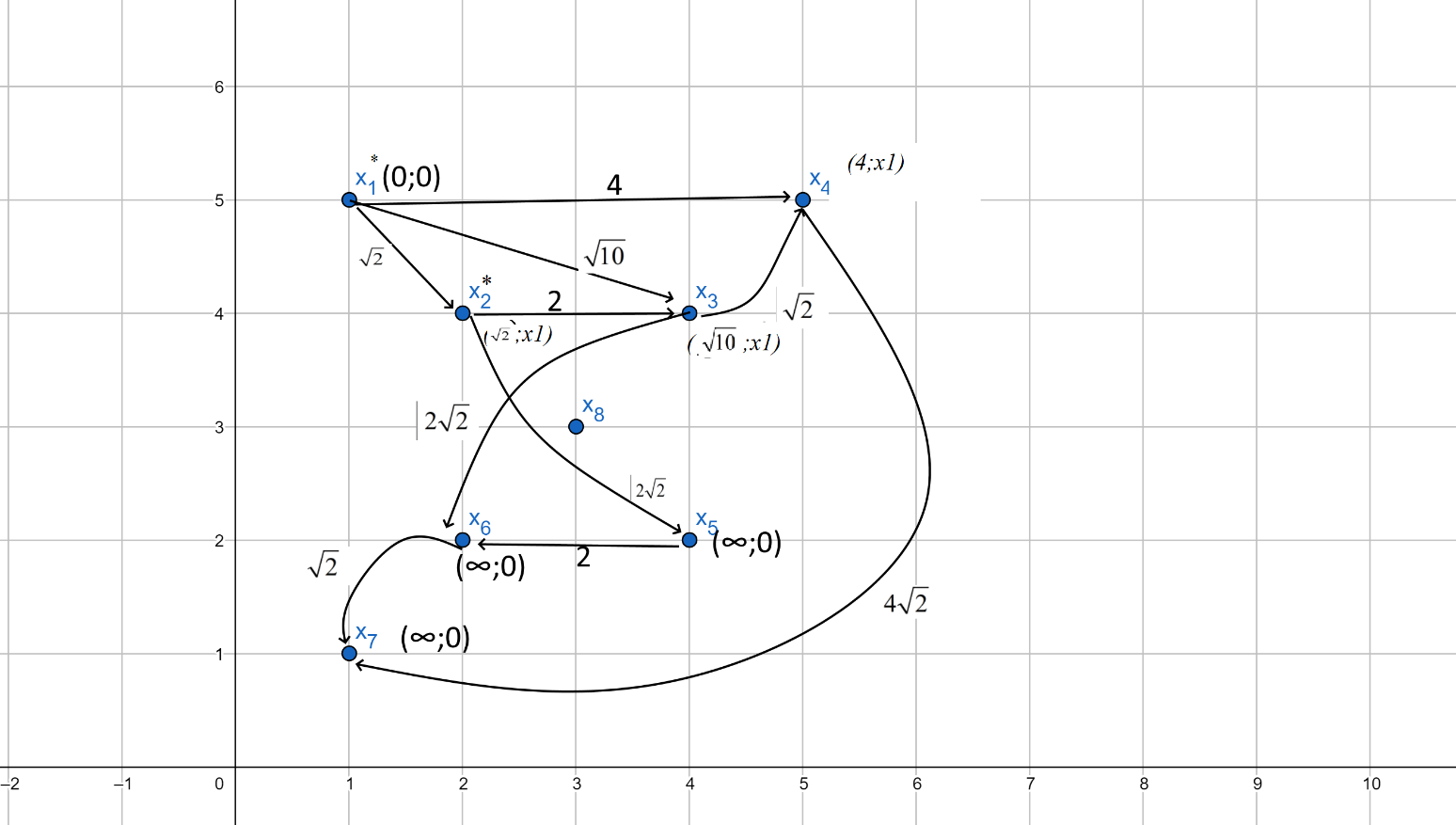
Вычислим расстояние до смежных с
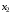 вершин:
вершин: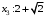
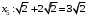 :
: Минимальное из расстояний
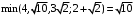 , поэтому вершина
, поэтому вершина  становится постоянной.
становится постоянной.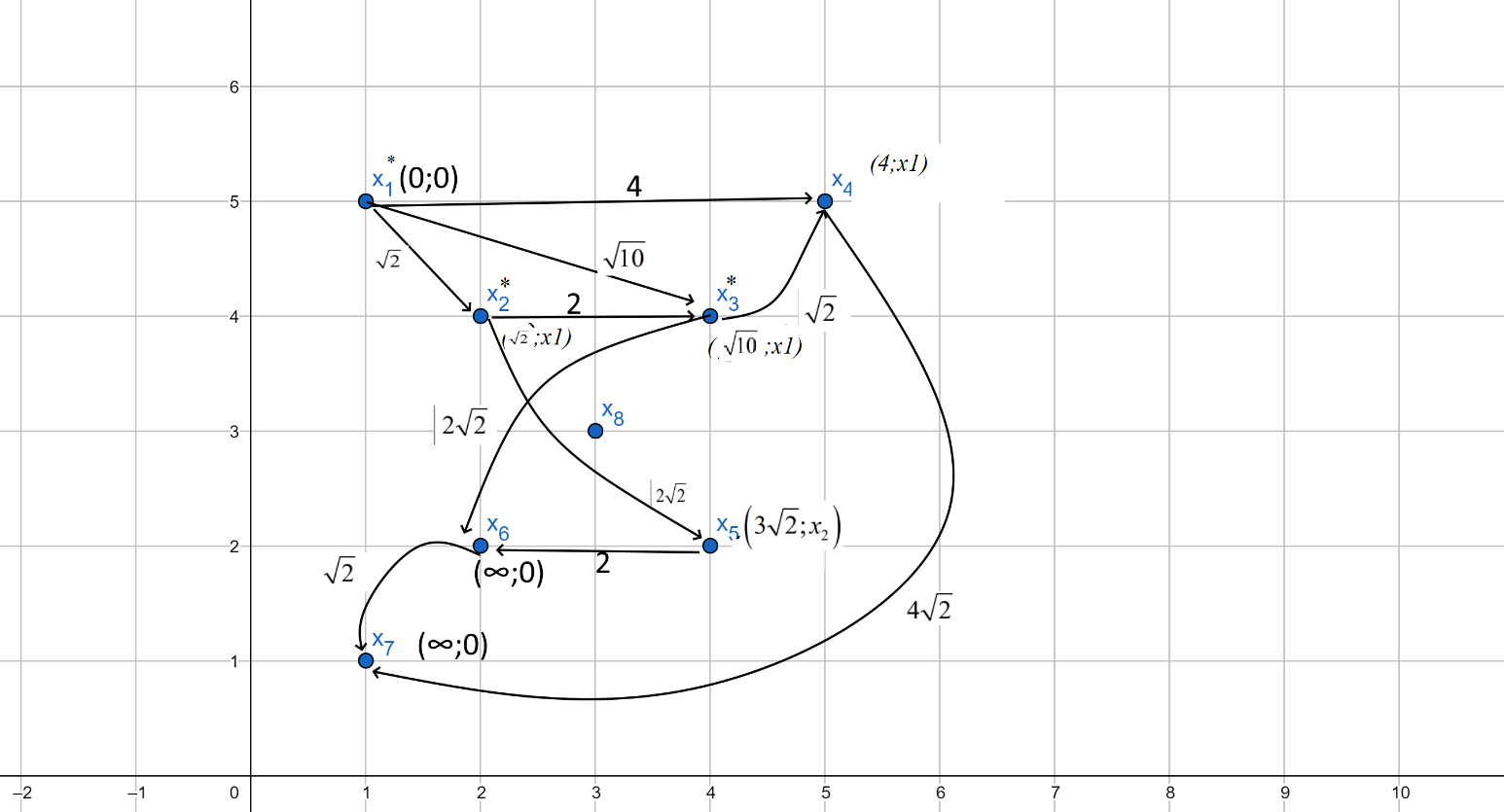
Вычислим расстояния от вершины
 до смежных вершин:
до смежных вершин: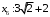
Вычислим расстояние от вершины
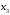 до смежных вершин:
до смежных вершин: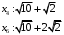
Поскольку
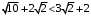 , то метка вершины
, то метка вершины 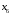 становится
становится 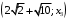
Минимальное из расстояний
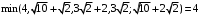 , поэтому вершина
, поэтому вершина 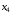 становится постоянной.
становится постоянной.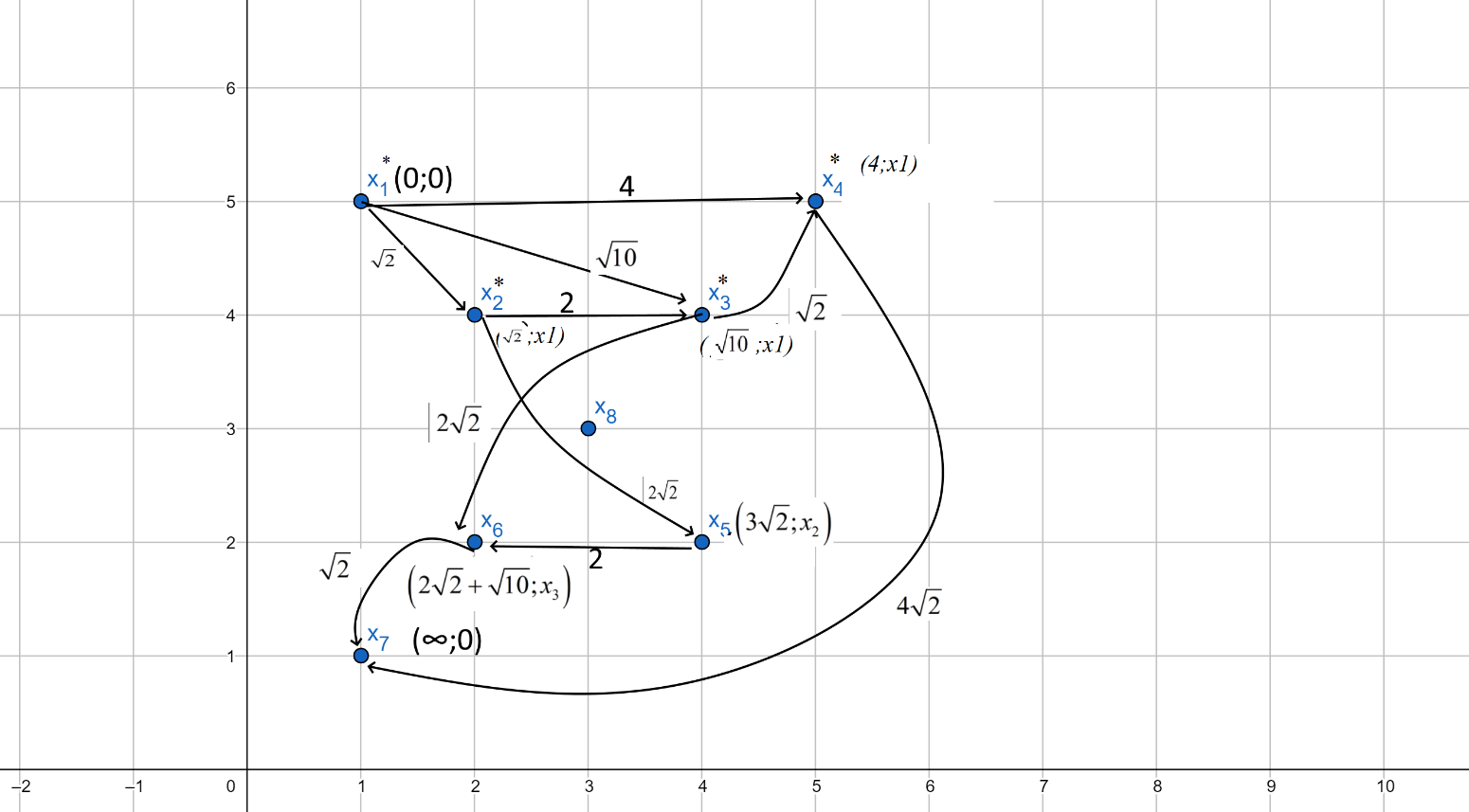
Вычислим расстояние от вершины
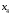 до вершины
до вершины 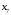 :
: 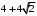 и от вершины
и от вершины 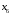 до вершины
до вершины 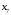 :
: 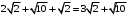 .
.Поскольку
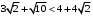 , то метка вершины
, то метка вершины 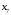
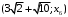
Минимальное из расстояний
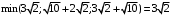 , поэтому вершина
, поэтому вершина 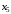 становится постоянной.
становится постоянной.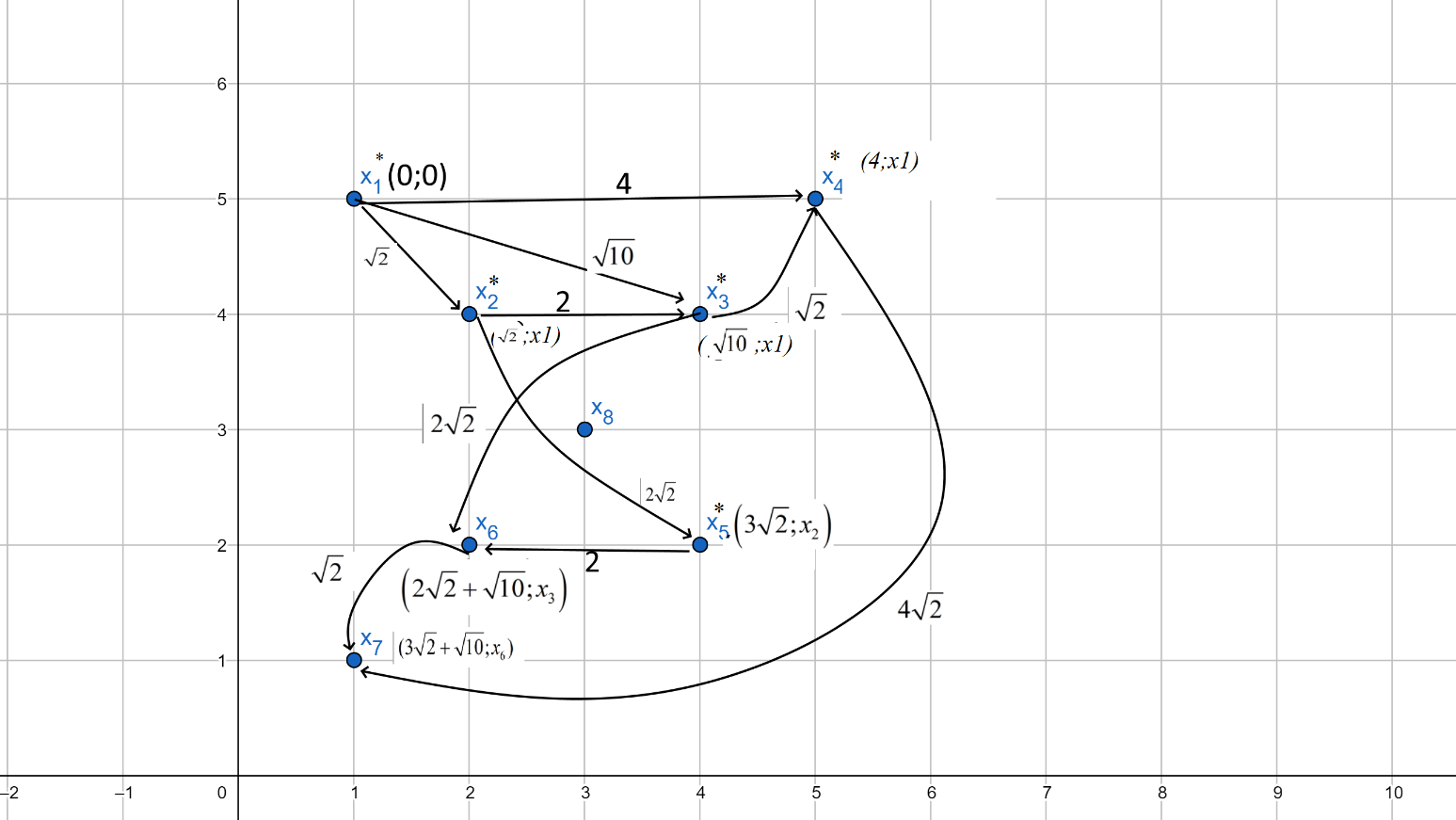
Таким образом, получены минимальные расстояния из вершины
 до остальных вершин:
до остальных вершин: :
: 
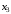 :
: 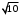
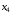 : 4
: 4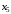 :
: 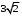
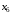 :
: 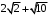
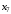 :
: 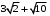

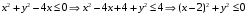
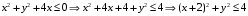
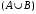 :
:
 имеет вид:
имеет вид: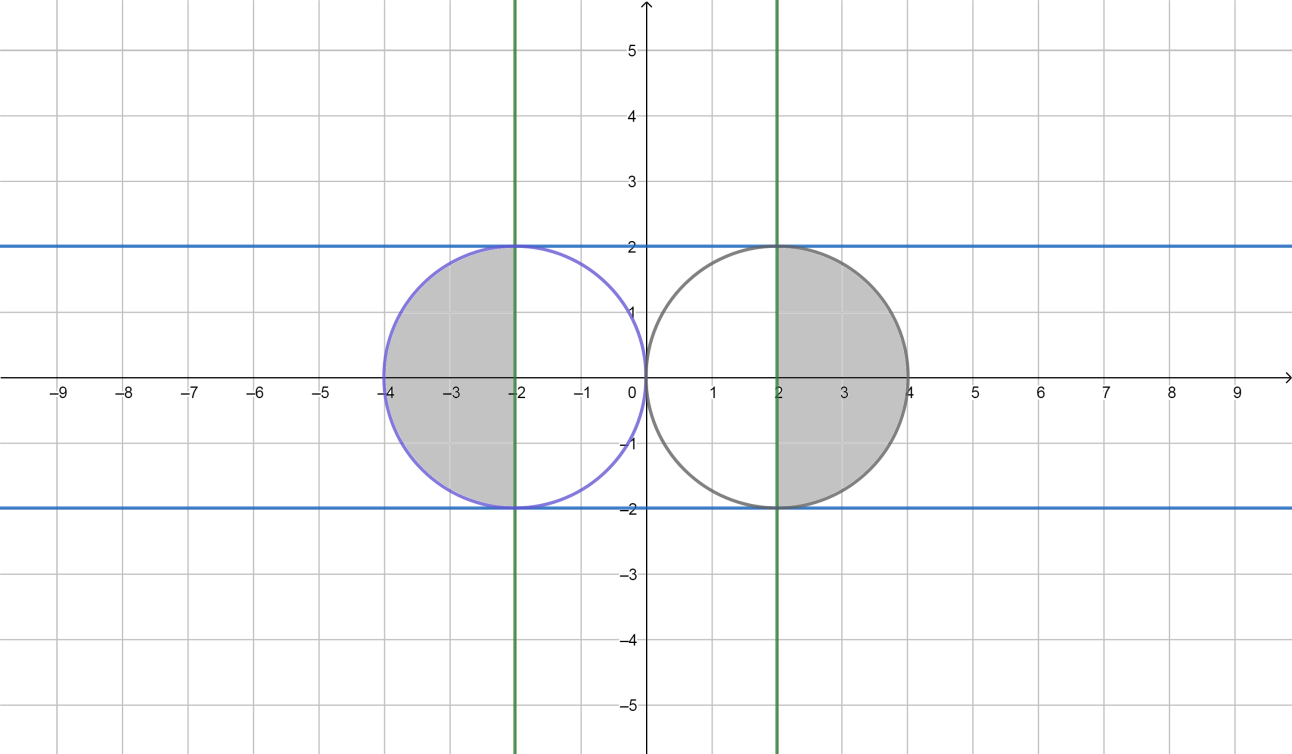
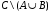 имеет вид:
имеет вид:
 имеет вид:
имеет вид: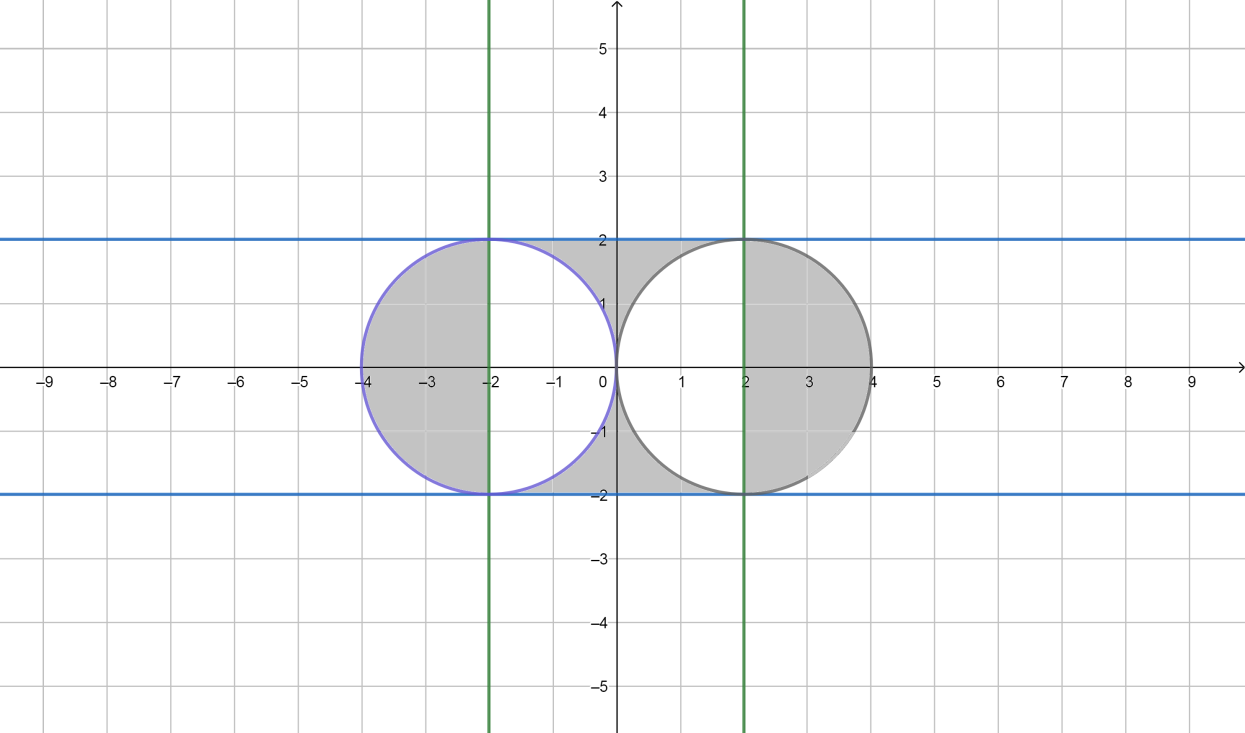

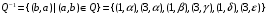
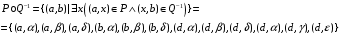
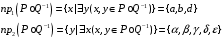
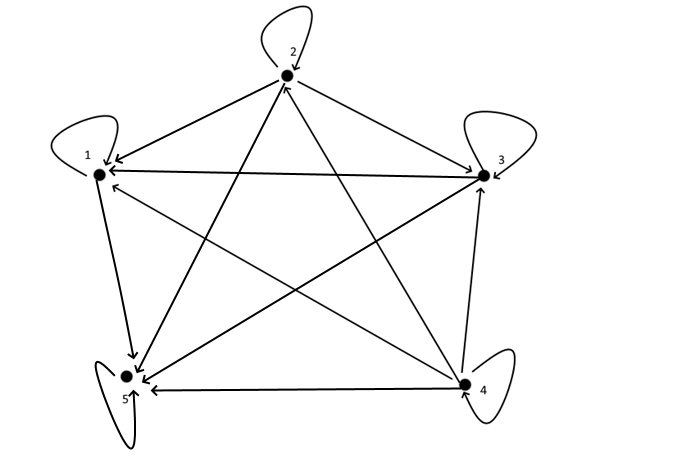
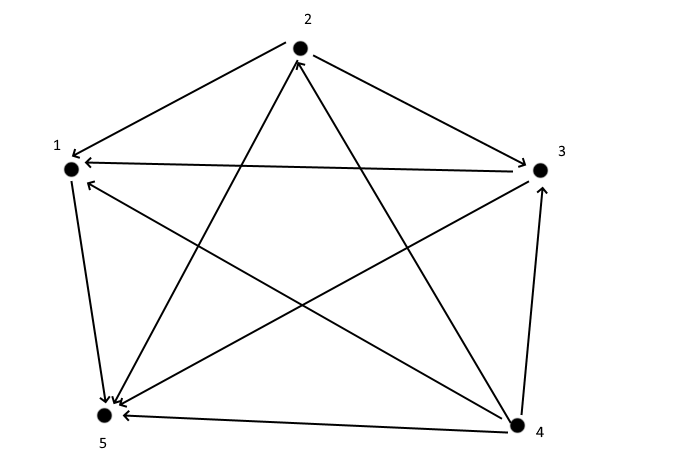
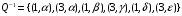 ,
, 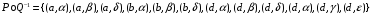 ,
,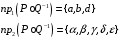

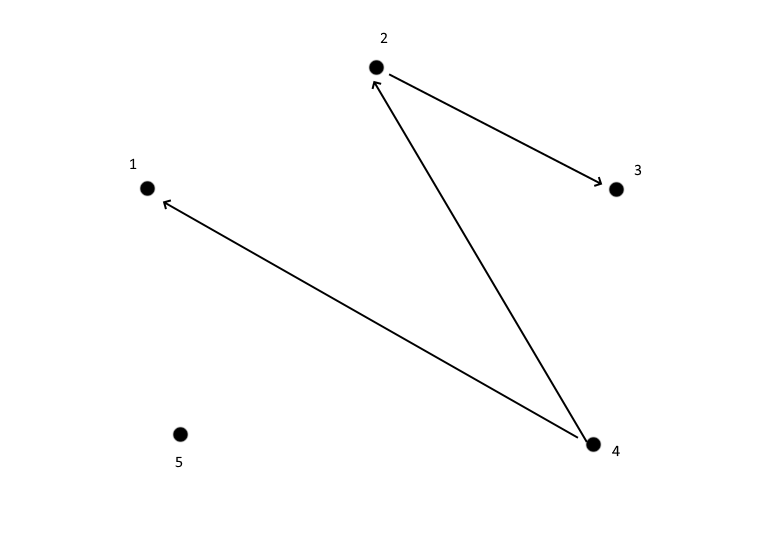
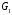 получаем, что этому отношению должны также принадлежать пары (4,4), (1,1), (2,2), (3,3), (5,5). Из того, что отношение симметрично, поскольку пары (4,1), (2,3), (4,2) принадлежат отношению
получаем, что этому отношению должны также принадлежать пары (4,4), (1,1), (2,2), (3,3), (5,5). Из того, что отношение симметрично, поскольку пары (4,1), (2,3), (4,2) принадлежат отношению 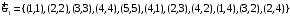
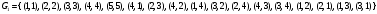
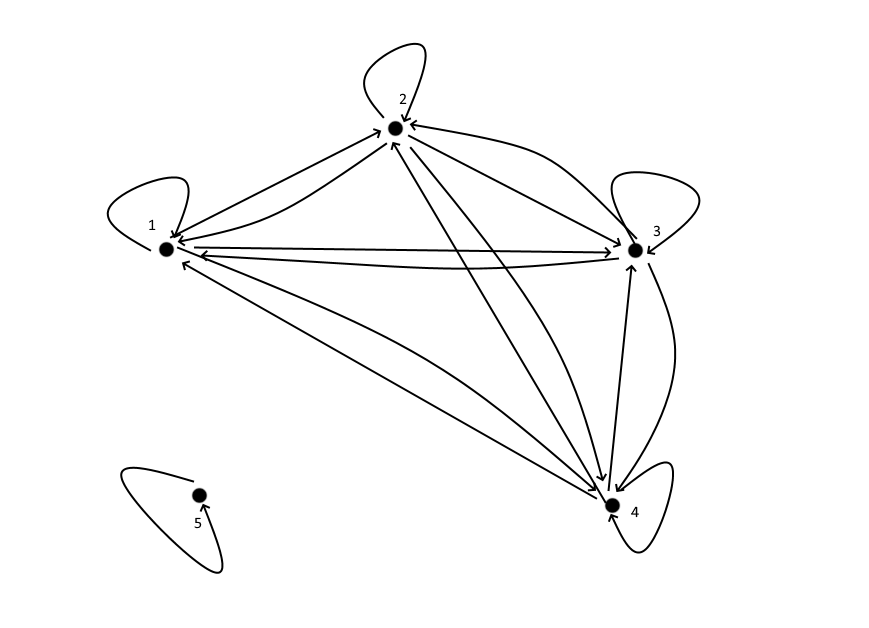
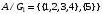
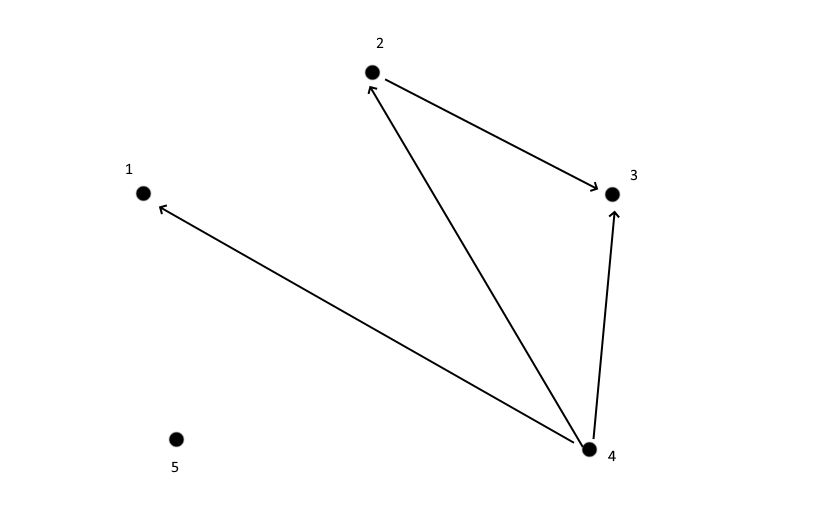
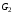 на основе
на основе 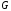 , путем добавления минимального количества новых пар, чтобы выполнялись условия рефлексивности, транзитивности, антисимметричности:
, путем добавления минимального количества новых пар, чтобы выполнялись условия рефлексивности, транзитивности, антисимметричности: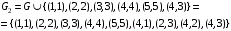
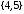
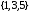
 на основе отношении
на основе отношении