Задачи, Выполнить деление комплексных чисел.. Математика-универ. Решение Решение Вычислить пределы последовательностей
 Скачать 48.5 Kb. Скачать 48.5 Kb.
|
|
Задачи 1. Выполнить деление комплексных чисел. 1.1 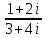 Решение: 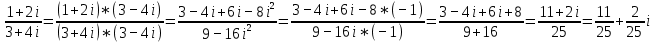 1.2. 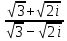 Решение: 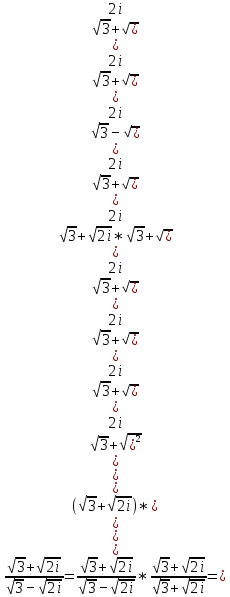 2. Вычислить пределы последовательностей. 2.1. 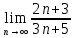 Решение: 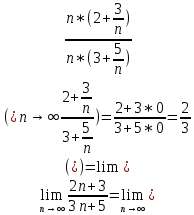  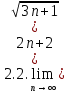  Решение: Решение: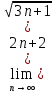  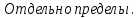 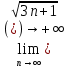  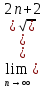  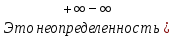 ) преобразуем выражение: ) преобразуем выражение: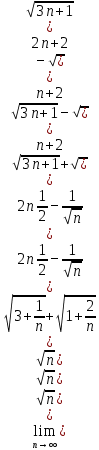    Вычислим пределы числителя и знаменателя отдельно. Вычислим пределы числителя и знаменателя отдельно.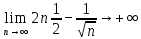  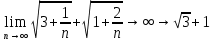 Так как выражение Так как выражение 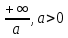 определено как определено как 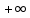 , предел , предел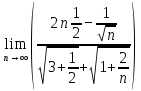 равен равен 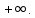 3. Используя признаки Даламбера и Коши исследовать сходимость рядов. 3.1. 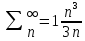 Решение: 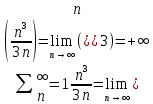 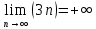 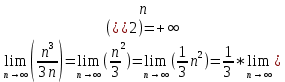 , сходится. , сходится.3.2. 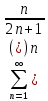 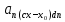 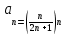 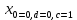 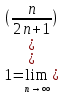 , не сходится , не сходится4. Найти производные сложных функций. 4.1. 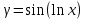 Решение: 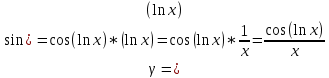  4.2. 4.2. 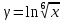 Решение: 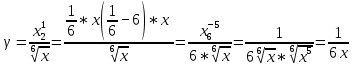   y yx 5. Вычислить неопределенный интеграл. 5.1. 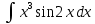 Решение: 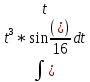 свойство интегралов: свойство интегралов: 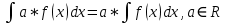 Далее решение: 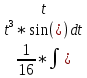 Метод интегрирования по частям: Метод интегрирования по частям: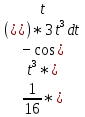 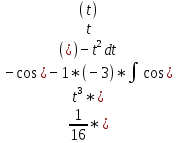 Любое выражение, умножение на -1, равно ему противоположному: 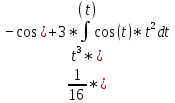 интегрирование по частям: интегрирование по частям: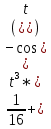 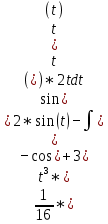 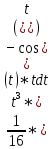 Переместительный закон, чтобы изменить порядок членов: Переместительный закон, чтобы изменить порядок членов: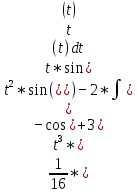 Интегрирование по частям: Интегрирование по частям: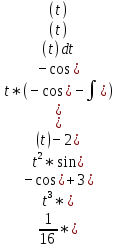 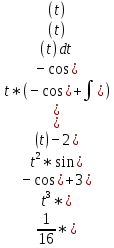  Использую Использую 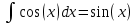 , найдем интеграл: , найдем интеграл: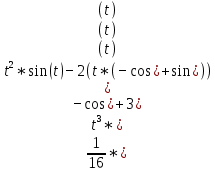 Обратная замена t=2x: 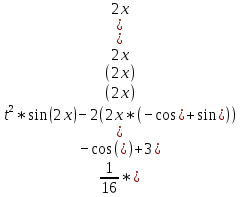  Упростим выражение: Упростим выражение: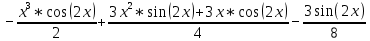 Прибавим константу интегрирования: Прибавим константу интегрирования: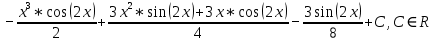  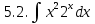 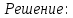 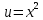 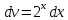 Вычислим дифференциал: 1) 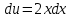 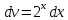 2) 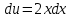 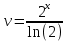 Подставим: 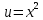 , , 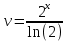 , , 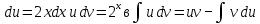 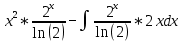 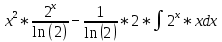 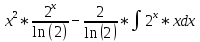 Переместительный закон: 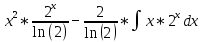 Интегрирование по частям: 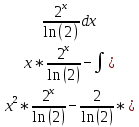 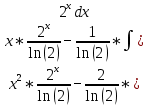 Используя 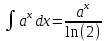 , найдем интеграл , найдем интеграл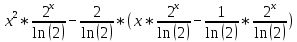 Упростим выражение: 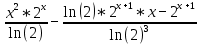 Решение: Решение: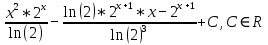 6. Найти частные производные первого и второго порядка. 6.1. 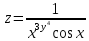 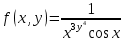 Производная по X: 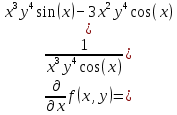 Производная по Y: 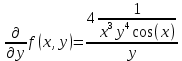 Производная по XX: 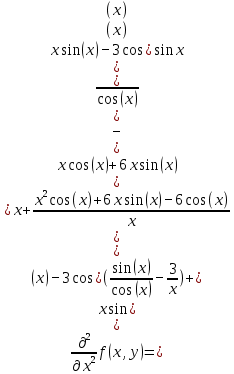 Производная по YY: 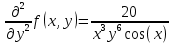 6.2. 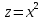 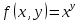 Производная по X: 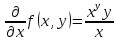 Производная по Y: 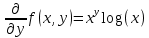 Производная по XX: 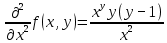 Производная по YY: Производная по YY: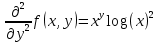 7. Найти сумму матриц. 7.1. 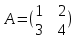 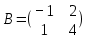 Решение: 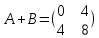 7.2. 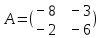 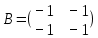 Решение: 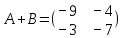 8. Найти произведение матриц. 8.1. 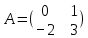 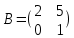 Решение: 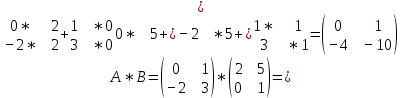 8.2. 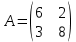 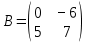 Решение: 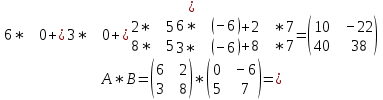 9. Найти определители матриц. 9.1. 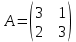 Решение: 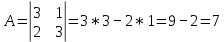 9.2. 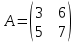 Решение: 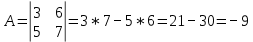 10. Решить систему уравнений. 10.1. 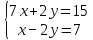 Решение: 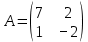 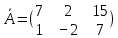 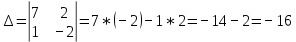 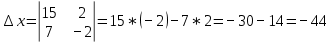 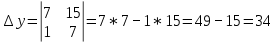 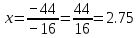 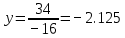 Ответ: (2,75; -2,725). Ответ: (2,75; -2,725).10.2. 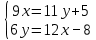 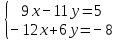 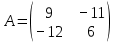 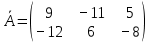 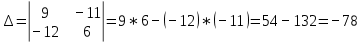 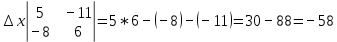 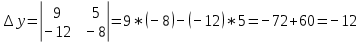 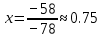 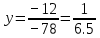 Ответ: ( 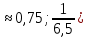 11. Для заданных векторов найти смешанное произведение 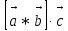 11.1. 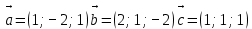 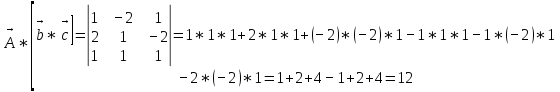 11.2 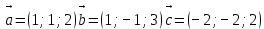 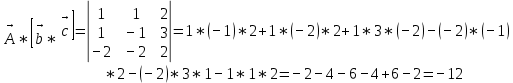 |
