Контрольная по ТОЭ. Контрольная.15.01.18.. Решение Рис Преобразование треугольникзвезда Сопротивления в преобразованой схеме (рис. 2) определяются из соотношений
 Скачать 247.4 Kb. Скачать 247.4 Kb.
|
|
Задача №1 Определить токи и напряжения каждого участка цепи постоянного тока, изображенной на рис.1 приняв метод преобразования треугольника сопротивлений в эквивалентную звезду сопротивлений и метод преобразования звезды сопротивлений в эквивалентный треугольник. Составьте баланс мощностей. Данные для расчета приведены в таблице 2. 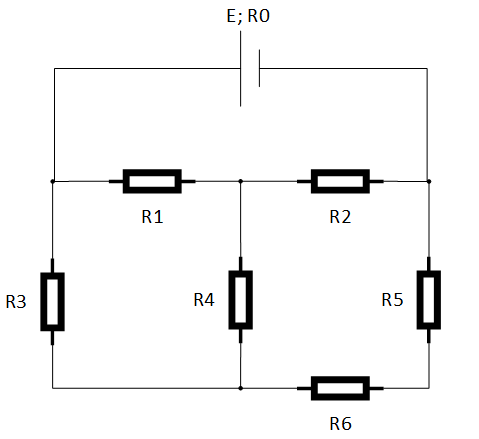 Рис.1. Исходная расчетная схема Решение 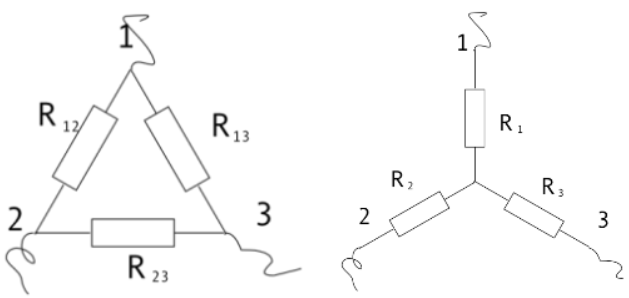 Рис.2. Преобразование треугольник-звезда Сопротивления в преобразованой схеме (рис.2) определяются из соотношений 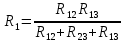 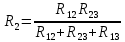 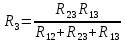 Обратное преобразование звезда-треугольник сопротивления определятся соотношениями 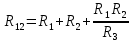 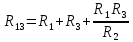 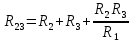 Преобразуем к примеру треугольник 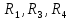 в эквивалентную звезду тогда преобразованная схема будет иметь вид (рис.3): в эквивалентную звезду тогда преобразованная схема будет иметь вид (рис.3):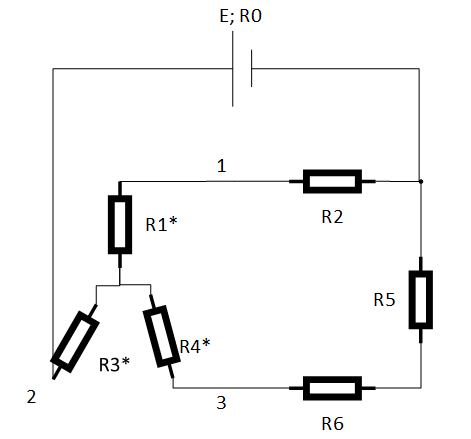 Рис.3. Эквивалентная расчетная схема после преобразования треугольника R1R3R4 в эквивалентную звезду. Для численных расчетов удобно использовать систему Mathcad. Начало документа Mathcad Исходные данные: 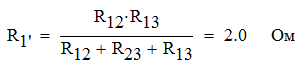 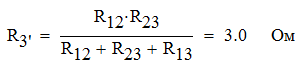 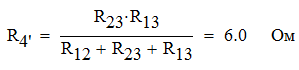 Составим уравнения по законам Кирхгофа. Открываем блок решения Для узла 1 по первому закону Кирхгофа (рис.4) имеем: Составляем уравнения по второму закону Кирхгофа Найдено решение системы 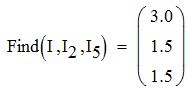 Полученные значения токов в ветвях (рис.4) 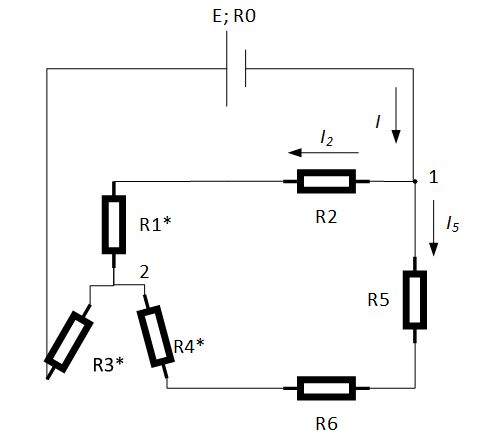 Рис.4. Составим баланс мощности: Баланс мощности сходится. Выполним расчет преобразуя звезду R1R2R4 (рис.1) в эквивалентный треугольник. 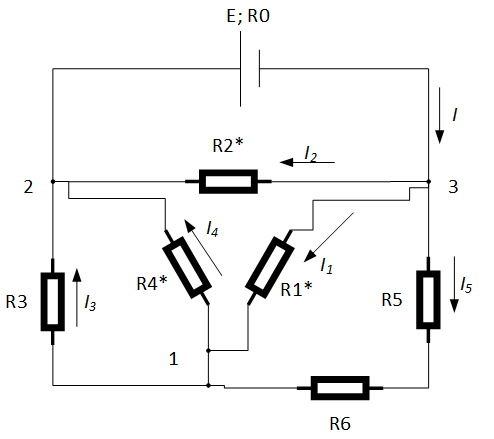 Рис.5. Эквивалентная расчетная схема после преобразования звезды R1R2R4 в эквивалентный треугольник. Открываем блок решения Составляем уравнения по законам Кирхгофа: Для узлов 1,2 по первому закону Кирхгофа имеем: Составляем уравнения по второму закону Кирхгофа Найдено решение системы: 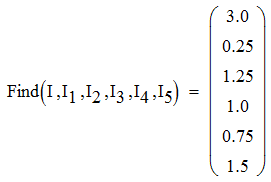 Полученные значения токов в ветвях (рис.5): Составляем баланс мощности Окончание документа Mathcad Задача №2 В цепь переменного тока параллельно включены катушка индуктивности с параметрами 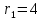 Ом и Ом и 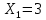 Ом и конденсатор Ом и конденсатор 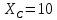 Ом. Потребляемая цепью мощность равна 16 Вт. Определить проводимости ветвей и всей цепи, токи ветвей и всей цепи, полную и реактивную мощность, коэффициент мощности цепи. Построить векторную диаграмму токов. Написать условие для наступления в цепи резонанса токов. Определить ток в цепи в этом случае. Ом. Потребляемая цепью мощность равна 16 Вт. Определить проводимости ветвей и всей цепи, токи ветвей и всей цепи, полную и реактивную мощность, коэффициент мощности цепи. Построить векторную диаграмму токов. Написать условие для наступления в цепи резонанса токов. Определить ток в цепи в этом случае.Решение 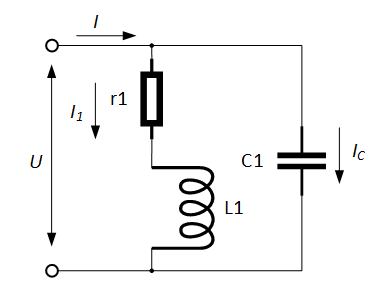 Рис.6. Исходная расчетная схема Все расчеты удобно произвести с помощью системы Mathcad Начало документа Mathcad Исходные данные Действующее значение тока ветви содержащей индуктивность 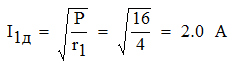 Модуль сопротивления ветви содержащей индуктивность Действующее значение напряжения цепи Комплекс сопротивления ветви содержащей индуктивность Комплекс проводимости ветви содержащей индуктивность 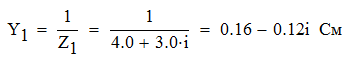 Комплекс сопротивления ветви содержащей емкость Комплекс проводимости ветви содержащей емкость 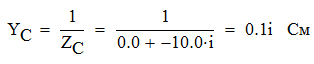 Комплекс сопротивления всей цепи 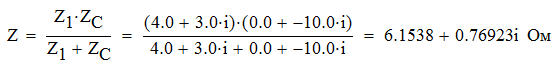 Комплекс проводимости цепи 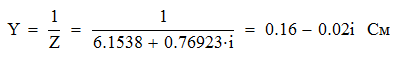 Комплекс тока ветви содержащей индуктивность 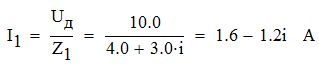 Комплекс тока ветви содержащей емкость 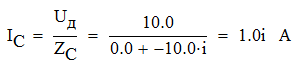 Комплекс тока цепи Комплекс полной мощности цепи Активная мощность цепи Реактивная мощность цепи Строим векторную диаграмму токов. Составляем вектор токов 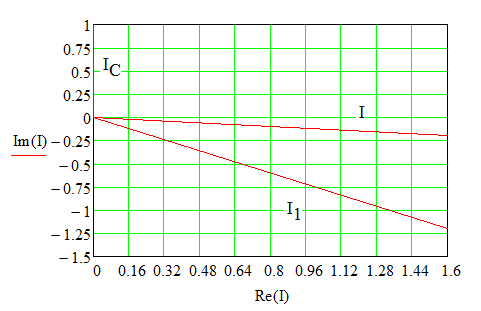 Рис.7. Векторная диаграмма токов в комплексной плоскости (x, jy) Условие возникновения резонанса токов 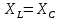 Для расчета зададимся частотой 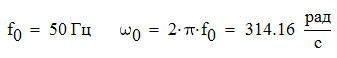 Определяем индуктивность 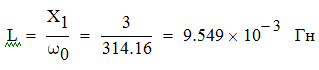 Определяем емкость 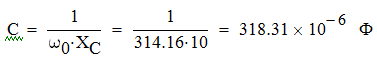 Резонансная частота 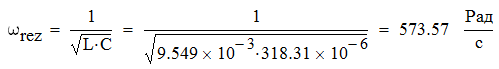 Резонансное индуктивное сопротивление Резонансное емкостное сопротивление 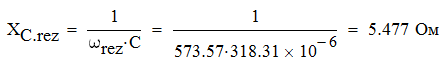 Рассчитаем резонансный ток, составим и решим систему 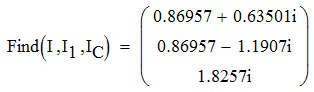 Комплекс тока при резонансе равен Действующее значение резонансного тока, равно: Окончание документа Mathcad На рис.8 выполнен частотный анализ цепи в среде NI Multisim, из которого видно, что действующее значение резонансного тока найдено верно. 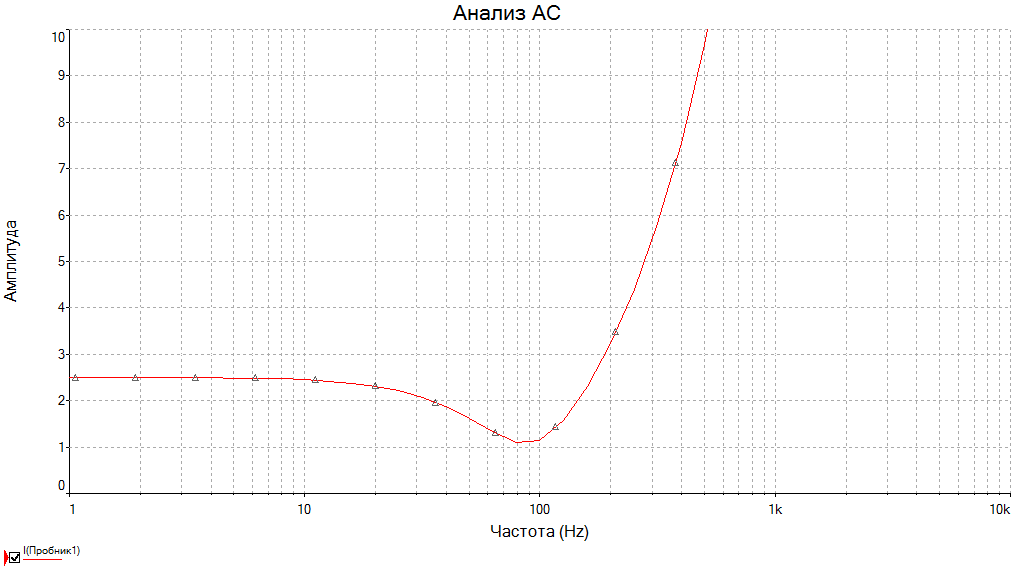 Рис.8. AC анализ цепи (NI Multisim) |
