Геометрия. геометрия 15.04. Решение s бок 12 p осн l p осн 4 а 45 20 см

• Название: Решение s бок 12 p осн l p осн 4 а 45 20 см
• Анкор: Геометрия
• Дата: 16.04.2022
• Размер: 24.22 Kb.
• Имя файла: геометрия 15.04.docx
• Тип: Решение; #478166

Площадь поверхности пирамиды

Площадью полной поверхности пирамиды называются сумма площадей всех ее граней, а площадью боковой поверхности пирамиды – сумма площадей ее боковых граней.

Для пирамиды, верно равенство S_полн= S_бок+S_осн.

Теорема. Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.

Задача 1. В правильной пирамиде высота боковой грани равна 12 см, а в основании лежит квадрат со стороной 5 см. Найти площадь боковой и полной поверхности пирамиды.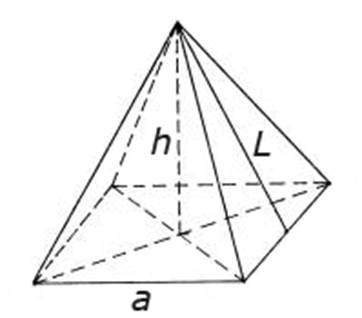



Решение

1. S_бок = 1/2 P_ОСН · l

2. P_ОСН =4· а = 4·5 = 20 см.

3. S_бок = 1/2 P_ОСН · L = 1/2· 20 · 12 = 120 см².

4. S_п.п. = S_бок + S_осн

5. S_осн  = а² = 5² = 25 см².

6. S_п.п. = S_бок + S_осн = 120 + 25 = 145 см².
Алгоритм решения задач на нахождение площади боковой и полной поверхности пирамиды:

1. 
   Определение вида пирамиды и ее элементного состава.
   
2. 
   Запись выражения для нахождения базовой формулы площади боковой поверхности пирамиды.
   
3. 
   Нахождение неизвестных элементов для вычисления площади боковой поверхности пирамиды.
   
4. 
   Вычисление площади боковой поверхности пирамиды.
   
5. 
   Запись выражения для нахождения базовой формулы площади полной поверхности пирамиды.
   
6. 
   Нахождение неизвестных элементов для вычисления площади полной поверхности пирамиды.
   
7. 
   Вычисление площади полной поверхности пирамиды.