УТС - пример. Решение с использованием символа операции дифференцирования (, см. Приложение п 4 в 1 и 2 ), записать данное уравнение в принятой для тау форме
 Скачать 141.79 Kb. Скачать 141.79 Kb.
|
|
Задание № 1 Динамика объекта управления, изображенного на рисунке функциональной схемой, 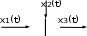 представлена следующим дифференциальным уравнением, записанным в неявном виде, 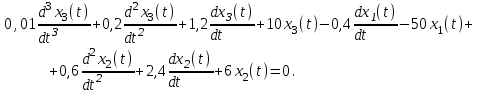 Решение: С использованием символа операции дифференцирования ( 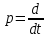 , см. Приложение П.1.4 в [1] и [2] ), записать данное уравнение в принятой для ТАУ форме , см. Приложение П.1.4 в [1] и [2] ), записать данное уравнение в принятой для ТАУ форме 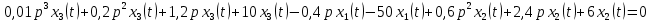 В принятой для ТАУ форме: 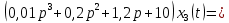 (0,4p+50) 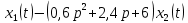 2. Преобразовать записанное в принятой для ТАУ форме дифференциальное уравнение к стандартному виду: а) 1-го типа, б) 2-го типа. а) 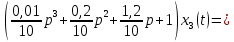 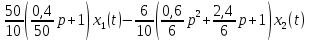 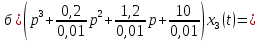 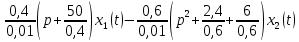 3. Записать характеристическое уравнение и по его коэффициентам оценить свойство устойчивости объекта 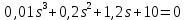 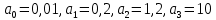 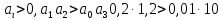 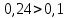 Условие выполнено, система устойчива 4. Записать уравнение установившегося статического режима объекта и построить графики его статических характеристик 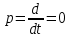 все производные равны все производные равны 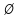 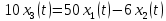   x3 x3 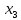    при при 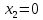   при при 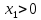 при 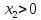    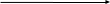  x1 x1 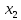 при 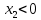 при 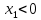  при при 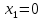   Задание № 2 Дифференциальное уравнение, описывающее динамику (неустановившееся состояние, см. [1], стр.45; [2], стр.27) линейной системы, имеет следующее характеристическое уравнение: а) 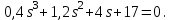 б) 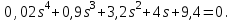 в) 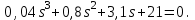 г) 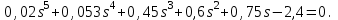 д) 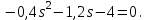 е) 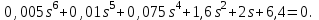 ж) 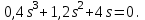 з) 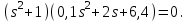 Требуется: 1. Для каждого варианта характеристического уравнения по его коэффициентам дать полное обоснованное заключение об устойчивости системы (см. разд. 4.4, 4.5 и 4.8 в [1], [2]) Решение: а) 0,4 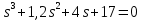 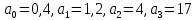 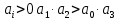 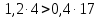 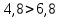 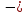 система неустойчивая система неустойчиваяб) 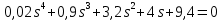 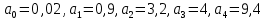 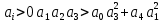 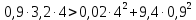 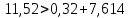 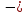 система устойчивая система устойчивая в) 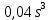 +0,8 +0,8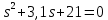 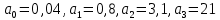 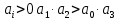 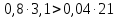 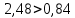 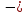 система устойчивая система устойчиваяг) 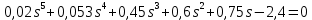 есть коэффициент со знаком «-» 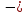 система неустойчивая система неустойчиваяд) 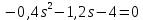 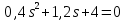 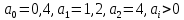 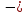 система устойчивая система устойчиваяe) 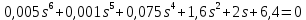 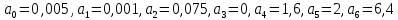 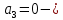 система неустойчивая система неустойчиваяж) 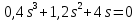 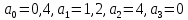 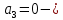 система неустойчивая система неустойчиваяз) ( 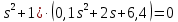 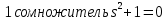 2 сомножитель 2 сомножитель 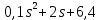 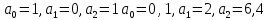  Задание № 3 Д 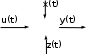 инамика системы, представленной на рисунке функциональной схемой, инамика системы, представленной на рисунке функциональной схемой,описывается дифференциальным уравнением: 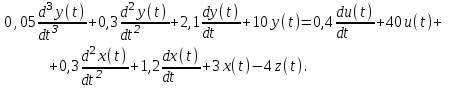 Решение: 1. Найти передаточные функции ( 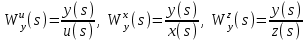 ) для выходного сигнала y(t) по каждому из 3-х входных сигналов – u(t), x(t), z(t). ) для выходного сигнала y(t) по каждому из 3-х входных сигналов – u(t), x(t), z(t). 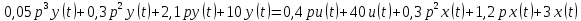 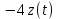 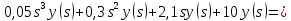 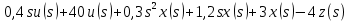 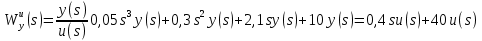  x(s) x(s)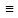 0 0  z(s) z(s)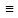 0 0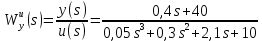 x(s) 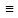 0 0 z(s) 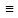 0 0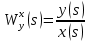 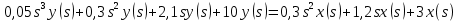 u(s) 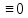 z 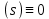 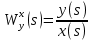 = =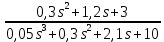 u(s) 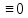 z 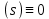 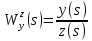 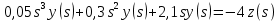 u(s) 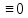 x(s) 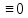 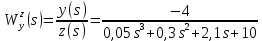 u(s) 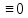 x(s) 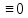 2. Преобразовать найденные передаточные функции к стандартному виду 2-го типа. Преобразование ПФ к стандартному виду 2-го типа 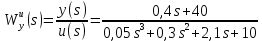 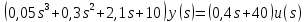 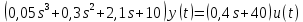 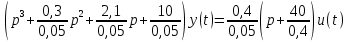 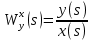 = =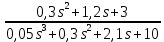 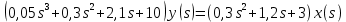 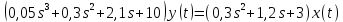 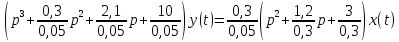 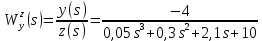 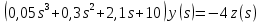 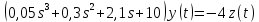 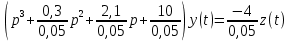 3. Изобразить структурную схему, соответствующую данному уравнению. U  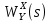 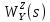   (s) (s)  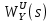 Y(s)  X(s) X(s)  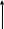 Z(s) Задание № 4 Динамическая система представлена следующей структурной схемой 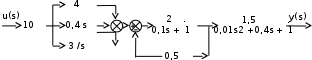 Решение: 1. Преобразовать структурную схему к виду 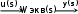 определив эквивалентную передаточную функцию 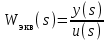 . .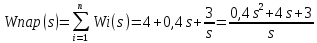 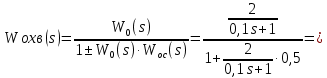 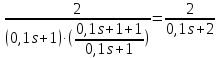 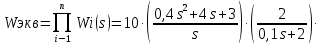 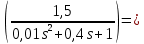 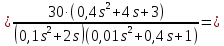 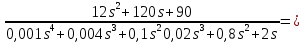 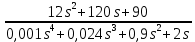 2. Оценка устойчивости системы по ПФ Wэкв(s) 0,001 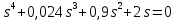 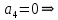 система не устойчивая. система не устойчивая.Задание № 5 Для исследуемой системы найдена эквивалентная передаточная функция следующего вида 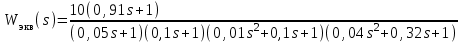 Решение:  1. По полюсам передаточной функции 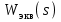 оценить устойчивость и корневые показатели качества – степень устойчивости и степень колебательности . оценить устойчивость и корневые показатели качества – степень устойчивости и степень колебательности .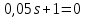 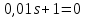 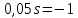 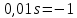 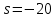 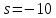 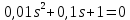 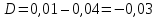 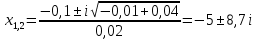 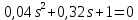 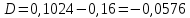 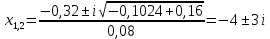       8 5   3 3      -20 -15 -10 -5   -3 -3-5   -8 -8  2. С помощью степени устойчивости оценить время переходного процесса системы при типовом ступенчатом входном сигнале . Оценка времени переходного процесса системы 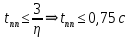 Задание № 6 Структурная схема контура привода, выходной вал которого нагружен инерционным, демпфирующим и позиционным моментами, имеет вид (возмущающее воздействие отсутствует)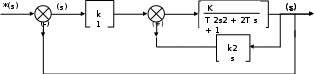 где К = 1,0 pад/В; Т = 10-2 с; k2 = 0,03 Вс; k1 = 9,0 В/pад ; = 0,5. Решение: 1. Преобразовать структурную схему к типовому виду . 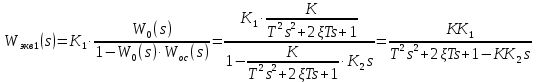  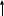  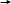 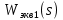   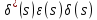 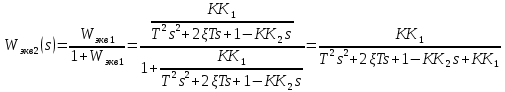  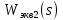  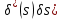 2. Для типовой структурной схемы найти в аналитическом виде передаточные функции привода в разомкнутом ( 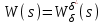 ) и замкнутом ( ) и замкнутом (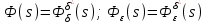 ) состояниях. ) состояниях.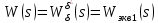 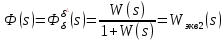 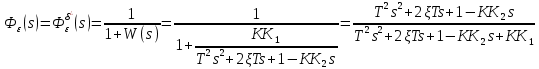 3. Представить найденные передаточные функции в числовом виде, определив значения их коэффициентов по заданным значениям параметров исходной структурной схемы. 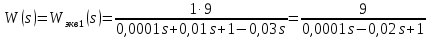 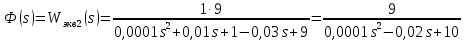 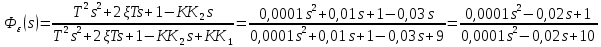 4. Оценить устойчивость привода в разомкнутом и замкнутом состояниях. Знаменатели ур-й приравниваем к 0: 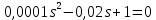  в каждом ур-ии есть знак «-» в каждом ур-ии есть знак «-»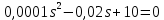 - система не устойчивая. - система не устойчивая.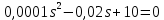 5. Определить величину статической ошибки и соответствующую ей величину установившегося значения выходного сигнала уст. 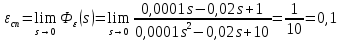 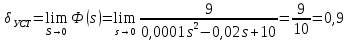 Записать диффеpенциальное уpавнение для замкнутого привода. 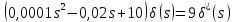 Задание № 7 П |
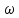 | 0 | … | 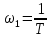 | … | 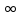 |
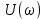 | 3 | | 1,5 | | 0   |
 | 0 | | -1,5 | | 0 |
 | 3 | |  | | 0 |
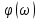 | 0 | | -45 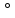 | | -90 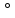 |
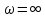 1,5
1,5 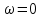 U
U


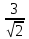 -45˚
-45˚ 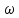

-1,5
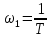
Оценить устойчивость замкнутой системы по АФЧХ разомкнутой системы, используя критерий Найквиста – Михайлова.
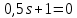
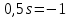
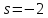
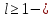 система не устойчивая.
система не устойчивая.6. Используя показательную форму записи Wр(j), получить выражения и построить качественный вид графиков логарифмических характеристик разомкнутой системы: L() – ЛАХ и () - ЛФЧХ.
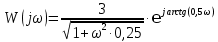
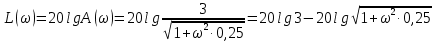 –ЛАХ
–ЛАХ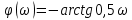 –ЛФЧХ
–ЛФЧХ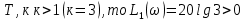 - прямая оси частот
- прямая оси частот на расстоянии от нее
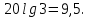
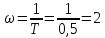
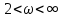 - область высоких частот
- область высоких частот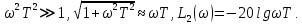
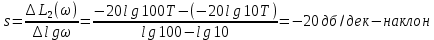
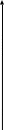 L(
L(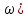
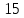
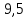
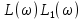


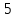
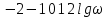

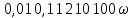
-10
-15
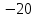 дб/дек
дб/дек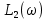
-20
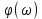
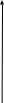
рад
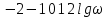
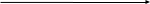
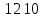
 102
102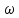
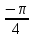
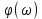
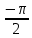
Используя полученное выражения для ЛАХ – L(), определить частоту среза с.
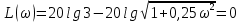
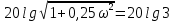
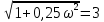
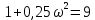
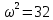
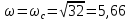 - частота среза.
- частота среза.Задание № 9
Частотная передаточная функция разомкнутой системы имеет вид
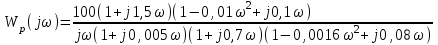
Решение:
Представить Wр(j) в показательной форме записи, воспользовавшись для нахождения модуля и аргумента данной частотной передаточной функции правилами алгебры комплексных функций
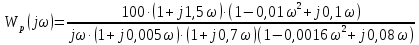
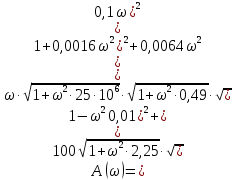
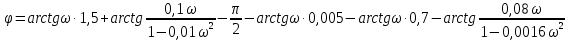
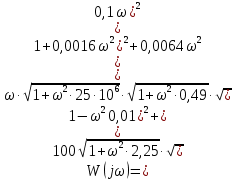
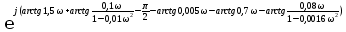
Задание № 10
Передаточная функция системы в разомкнутом состоянии имеет вид
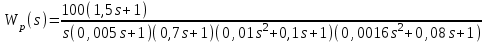
Решение:
Изобразить качественный вид графика асимтотической ЛАХ, воспользовавшись формализованным алгоритмом построения ЛАХ по передаточной функции.
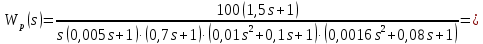
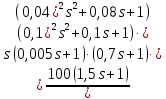
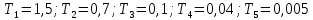
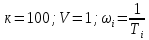
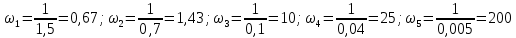
A(1;20
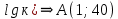
2. Определить приближенно по построенному графику интервал частот, в котором располагается частота среза с.
По графику:
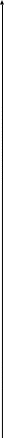
L
 (
(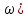
-20
 0
0

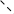 40 В
40 В  А
А-20
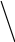 20 -60
20 -60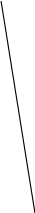


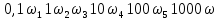
-20дб/дек
-20
-40
-100
-40
-60
-60
-80
-80
-100
 -100
-100-120
-120
-120
Задание № 11
Математическая модель pазомкнутого канала упpавления включает:
- уpавнение углового движения объекта управления
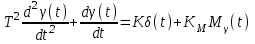 ;
;- уpавнение пpивода с оpганом упpавления
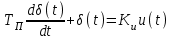 ,
,где T = 2 с, K = 70 с-1, KМ = 0,01 (Нмс)-1, TП = 0, 1 с, Кu = 0,05 pад/В,
M(t) – возмущающее воздействие (возмущающий момент)
Решение:
1.Записать уpавнения в опеpатоpной фоpме, pазpешить их относительно выходных сигналов ((s) и (s)) и пpедставить их в виде стpуктуpных схем.
Для первого уравнения
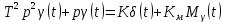
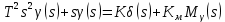
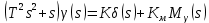
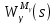

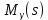
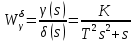
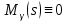
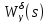
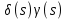
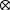



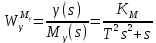
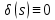
Для второго уравнения
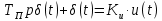

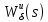

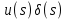
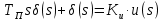
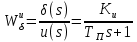
Составить стpуктуpную схему для pазомкнутого канала упpавления.
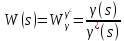
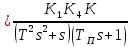 -ПФ разомкнутой системы
-ПФ разомкнутой системы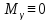
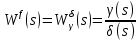
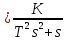 - ПФ разомкнутой системы
- ПФ разомкнутой системы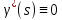 по возмущению.
по возмущению. 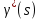
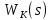
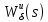
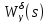
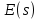
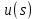
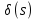
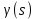





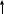
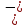
Составить стpуктуpную схему замкнутого канала управления, пpиняв сигнал ошибки (s) = *(s) - (s) и включив последовательное коppектиpующее звено с передаточной функцией
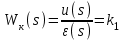
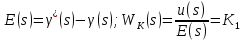
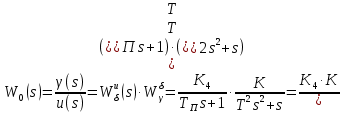
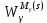
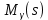

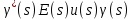
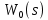
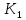





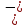
Г.О.С.
Преобразовать получившуюся стpуктуpную схему к типовому виду структурной схемы системы автоматического управления (САУ), для которой найти пеpедаточные функции САУ в pазомкнутом ( W(s), WM(s) ) и замкнутом (Ф(s), ФM(s), Ф (s), Ф M(s)) состояниях.
В разомкнутом состоянии:
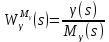
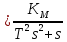
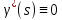
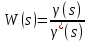
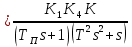
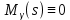
В замкнутом состоянии:
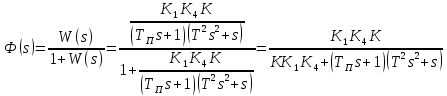
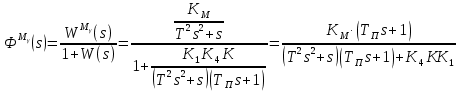
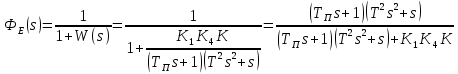
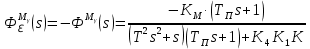
Из условия устойчивости замкнутой системы выбpать значение коэффициента k1
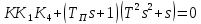
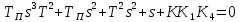
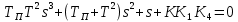

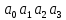
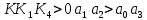
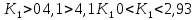
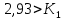
6. Пpи выбpанном значении k1:
6.1) оценить устойчивость САУ в pазомкнутом и замкнутом состояниях:
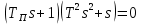
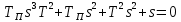
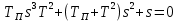
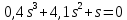
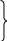
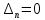 разомкнутая система
разомкнутая система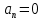 нейтрально устойчивая.
нейтрально устойчивая.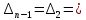
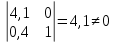
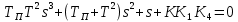 при
при 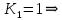
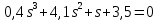
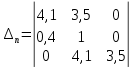
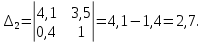
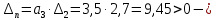 замкнутая система устойчивая.
замкнутая система устойчивая.6.2) оценить величину статической ошибки пpи * (t) = 1(t) и M(t) = 0
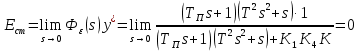
- астатическая САУ
6.3) найти установившееся значение выходного сигнала замкнутой САУ пpи входных сигналах * (t) = 0 и M(t)= M o1(t), где M o = 2,0 Нм
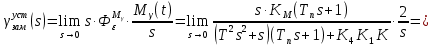
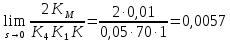
6.4) найти установившееся значение выходного сигнала разомкнутой САУ пpи входных сигналах * (t) = 0 и M(t)= M o1(t), где M o = 2,0 Нм
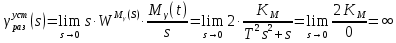

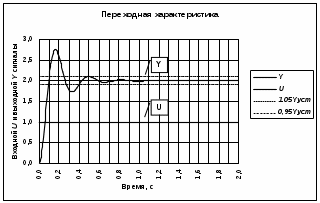 ереходная характеристика системы имеет вид, показанный на рисунке.
ереходная характеристика системы имеет вид, показанный на рисунке.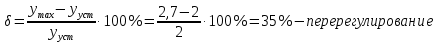
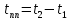
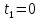
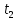 соответствует моменту начинания с которого выполняется для всех
соответствует моменту начинания с которого выполняется для всех 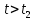 :
: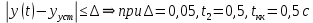
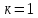 - колебательность (число полных колебаний y(t) относительно
- колебательность (число полных колебаний y(t) относительно 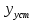 за время переходного процесса).
за время переходного процесса).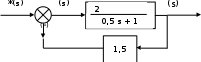
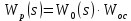
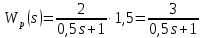
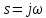
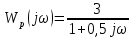 – исходная форма
– исходная форма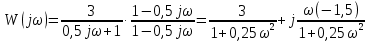 – алгебраическая
– алгебраическая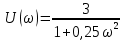
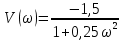
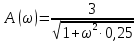
 jV
jV