Решение систем линейных уравнений
 Скачать 1.23 Mb. Скачать 1.23 Mb.
|
|
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ МОСКОВСКОЙ ОБЛАСТИ Кафедра информационных технологий Кафедра высшей математики КУРСОВАЯ РАБОТА ПО ЛИНЕЙНОЙ АЛГЕБРЕ И ГЕОМЕТРИИ ТЕМА: Решение систем линейных уравнений Содержание Введение Теоретическая часть Основные понятия Метод обратной матрицы Метод Гаусса Практическая часть Решение (метод Гаусса) Решение (метод обратной матрицы) Вывод Список литературы ВведениеРешение систем линейных алгебраических уравнений (СЛАУ) — одна из основных задач вычислительной линейной алгебры. Хотя задача решения системы линейных уравнений сравнительно редко представляет самостоятельный интерес для приложений, от умения эффективно решать такие системы часто зависит сама возможность математического моделирования самых разнообразных процессов с применением ЭВМ. Значительная часть численных методов решения различных (в особенности ─ нелинейных) задач включает в себя решение систем линейных уравнений как элементарный шаг соответствующего алгоритма. Одна из трудностей практического решения систем большой размерности связанна с ограниченностью оперативной памяти ЭВМ. Хотя объем оперативной памяти вновь создаваемых вычислительных машин растет очень быстро, тем не менее, еще быстрее возрастают потребности практики в решении задач все большей размерности. В значительной степени ограничения на размерность решаемых систем можно снять, если использовать для хранения матрицы внешние запоминающие устройства. Однако в этом случае многократно возрастают как затраты машинного времени, так и сложность соответствующих алгоритмов. Поэтому при создании вычислительных алгоритмов линейной алгебры большое внимание уделяют способам компактного размещения элементов матриц в памяти ЭВМ. К счастью, приложения очень часто приводят к матрицам, в которых число ненулевых элементов много меньше общего числа элементов матрицы. Такие матрицы принято называть разреженными. Одним из основных источников разреженных матриц являются математические модели технических устройств, состоящих из большого числа элементов, связи между которыми локальны. Простейшие примеры таких устройств ─ сложные строительные конструкции и большие электрические цепи. Известны примеры решенных в последние годы задач, где число неизвестных достигало сотен тысяч. Постановка задачиЦель: Решить СЛАУ методами «Гаусса»( «1»); и «обратной матрицы»( «2»). Исходные данные: Задание вариант № 2; Конспект лекций по линейной алгебре и геометрии; Учебники по линейной алгебре и геометрии; Офисные электронные приложения MS Word, MS Excel; Math Cad Задачи: Изучить теоретический материал «», «»; Решить СЛАУ методом «1»; Решить СЛАУ методом «2»; Решить СЛАУ при помощи встроенных функций MS Excel; Оформить КР с учетом методических указаний; Априорные представления о модели: Система линейных алгебраических уравнений размером 8*8 Результаты Получены решения СЛАУ методами «1» и «2»; Критерии оценки результата Методом «1» и метод «2» дают одинаковый результаты; Полученные результаты при подставлении в исходную систему линейных алгебраических уравнений давали правильное решение. Систему линейных уравнений записать в матричной форме и решить с помощью метода Гаусса и обратной матрицы. Теоретическая часть Основные понятияУравнение называется линейным, если оно содержит неизвестные только в первой степени и не содержит произведений неизвестных, т.е. если оно имеет вид: 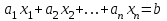 , ,где 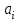 ( (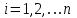 ), ), 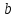 – числа. – числа.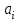 называются коэффициентами уравнения, называются коэффициентами уравнения, 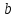 называется свободным членом. Если называется свободным членом. Если 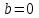 , то уравнение называется однородным. В противном случае уравнение называется неоднородным. , то уравнение называется однородным. В противном случае уравнение называется неоднородным.В этом параграфе мы будем рассматривать систему 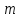 линейных уравнений с линейных уравнений с 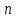 неизвестными, т.е. систему вида: неизвестными, т.е. систему вида: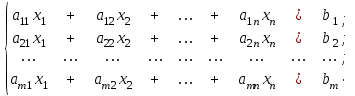 (1) (1)Обозначим через А и А* следующие матрицы: 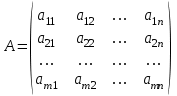 и и 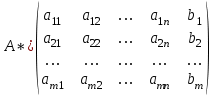 . .Матрицу А называют основной матрицей системы (1), а матрицу А* – расширенной матрицей системы (1). Пусть X – матрица-столбец неизвестных, B – матрица-столбец свободных членов, т.е. 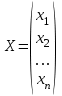 и и 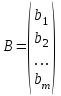 . .Тогда систему (1) можно записать в виде матричного уравнения A*X = B. Его называют матричной формой системы (1). Упорядоченный набор чисел 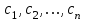 называется решением системы (1), если он обращает в тождество каждое уравнение системы. Если система линейных уравнений имеет хотя бы одно решение, то ее называют совместной. Система линейных уравнений, не имеющая решений, называется несовместной. называется решением системы (1), если он обращает в тождество каждое уравнение системы. Если система линейных уравнений имеет хотя бы одно решение, то ее называют совместной. Система линейных уравнений, не имеющая решений, называется несовместной.Если система совместна, то она имеет либо одно решение, либо множество решений. Система, имеющая единственное решение, называется определенной. Система, имеющая множество решение, называется неопределенной. Критерии совместности и определенности системы дают следующие две теоремы. ТЕОРЕМА (Кронекера–Капелли). Система линейных уравнений (1) совместна тогда и только тогда, когда ранг матрицы системы равен рангу ее расширенной матрицы, т.е. 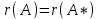 . .ТЕОРЕМА (критерий единственности решения). Система линейных уравнений (1) имеет единственное решение тогда и только тогда, когда ранг матрицы системы равен рангу ее расширенной матрицы и равен числу переменных, т.е. 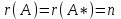 . .Метод обратной матрицыРассмотрим квадратную матрицу 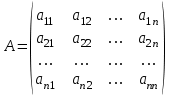 (1.1) (1.1) вычислительный алгебра система уравнений Обозначим D = det A. Квадратная матрица А называется невырожденной, или неособенной, если ее определитель отличен от нуля, и вырожденной, или особенной, если = 0. Квадратная матрица В называется обратной для квадратной матрицы А того же порядка, если их произведение А В = В А = Е, где Е ─ единичная матрица того же порядка, что и матрицы А и В. ТЕОРЕМА Для того, чтобы матрица А имела обратную, необходимо и достаточно, чтобы ее определитель был отличен от нуля. Матрица, обратная матрице А, обозначается через А1, так что В = А1. Обратная матрица вычисляется по формуле 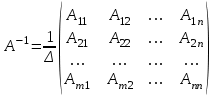 где А i j ─ алгебраические дополнения элементов a i j. Вычисление обратной матрицы для матриц высокого порядка очень трудоемко, поэтому на практике бывает удобно находить обратную матрицу с помощью метода элементарных преобразований (ЭП). Любую неособенную матрицу А путем ЭП только столбцов (или только строк) можно привести к единичной матрице Е. Если совершенные над матрицей А ЭП в том же порядке применить к единичной матрице Е, то в результате получится обратная матрица. Удобно совершать ЭП над матрицами А и Е одновременно, записывая обе матрицы рядом через черту. Отметим еще раз, что при отыскании канонического вида матрицы с целью нахождения ее ранга можно пользоваться преобразованиями строк и столбцов. Если нужно найти обратную матрицу, в процессе преобразований следует использовать только строки или только столбцы. Метод ГауссаЗапишем систему Ax=f, в развернутом виде 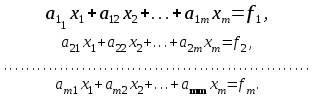 Метод Гаусса состоит в последовательном исключении неизвестных из этой системы. Предположим, что 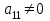 . Последовательно умножая первое уравнение на . Последовательно умножая первое уравнение на 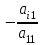 и складывая с i – м уравнение, исключим и складывая с i – м уравнение, исключим 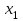 из всех уравнений кроме первого. Получим систему из всех уравнений кроме первого. Получим систему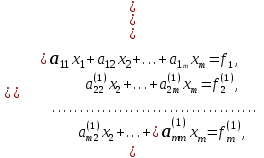 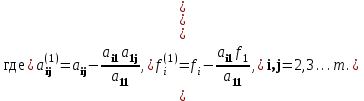 Аналогичным образом из полученной системы исключим 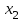 . Последовательно, исключая все неизвестные, получим систему треугольного вида . Последовательно, исключая все неизвестные, получим систему треугольного вида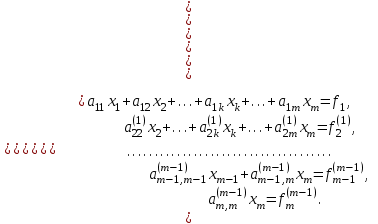 Описанная процедура называется прямым ходом метода Гаусса. Заметим, что ее выполнение было возможно при условии, что все 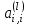 , , 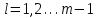 не равны нулю. не равны нулю.Выполняя последовательные подстановки в последней системе, (начиная с последнего уравнения) можно получить все значения неизвестных. 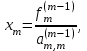  . .Эта процедура получила название обратный ход метода Гаусса. Метод Гаусса может быть легко реализован на компьютере. При выполнении вычислений, как правило, не интересуют промежуточные значения матрицы А. Поэтому численная реализация метода сводится к преобразованию элементов массива размерности (m×(m+1)), где m+1 столбец содержит элементы правой части системы. Для контроля ошибки реализации метода используются так называемые контрольные суммы. Схема контроля основывается на следующем очевидном положении. Увеличение значения всех неизвестных на единицу равносильно замене данной системы контрольной системой, в которой свободные члены равны суммам всех коэффициентов соответствующей строки. Создадим дополнительный столбец, хранящий сумму элементов матрицы по строкам. На каждом шаге реализации прямого хода метода Гаусса будем выполнять преобразования и над элементами этого столбца, и сравнивать их значение с суммой по строке преобразованной матрицы. В случае не совпадения значений счет прерывается. Один из основных недостатков метода Гаусса связан с тем, что при его реализации накапливается вычислительная погрешность. Для больших систем порядка m число действий умножений и делений близко к 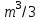 . .Для того чтобы уменьшить рост вычислительной погрешности применяются различные модификации метода Гаусса. Например, метод Гаусса с выбором главного элемента по столбцам, в этом случае на каждом этапе прямого хода строки матрицы переставляются таким образом, чтобы диагональный угловой элемент был максимальным. При исключении соответствующего неизвестного из других строк деление будет производиться на наибольший из возможных коэффициентов и, следовательно, относительная погрешность будет наименьшей. Существует метод Гаусса с выбором главного элемента по всей матрице. В этом случае переставляются не только строки, но и столбцы1. Использование модификаций метода Гаусса приводит к усложнению алгоритма увеличению числа операций и соответственно к росту времени счета. Поэтому целесообразность выбора того или иного метода определяется непосредственно программистом. Выполняемые в методе Гаусса преобразования прямого хода, приведшие матрицу А системы к треугольному виду позволяют вычислить определитель матрицы: 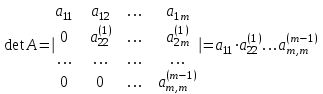 . .Метод Гаусса позволяет найти обратную матрицу. Для этого необходимо решить матричное уравнение 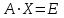 , ,где Е– единичная матрица. Его решение сводится к решению m систем 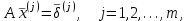 у вектора 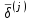 j ─я компонента равна единице, а остальные компоненты равны нулю. j ─я компонента равна единице, а остальные компоненты равны нулю.Практическая частьРешить данную систему линейных алгебраических уравнений методом Гаусса и методом обратной матрицы. |

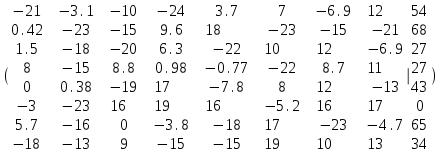
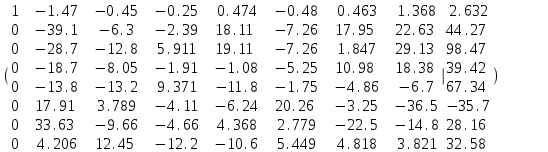
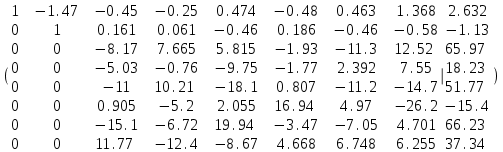
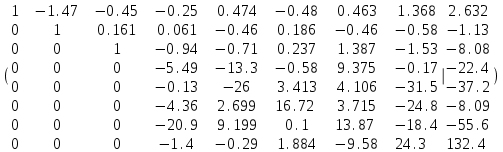
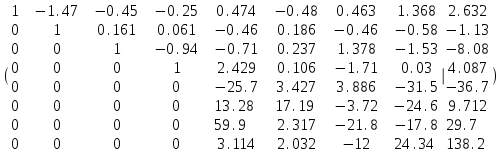
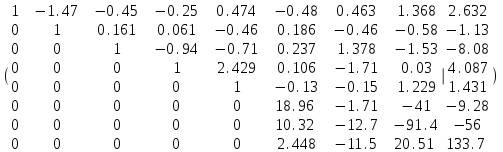
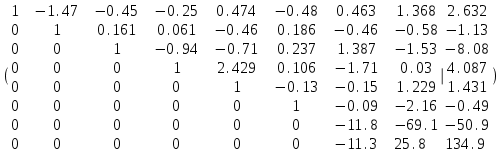
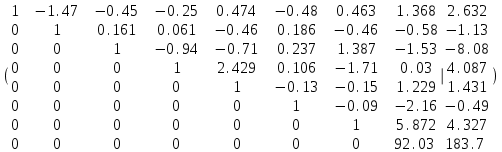
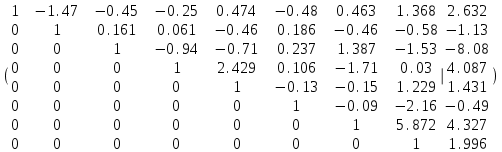
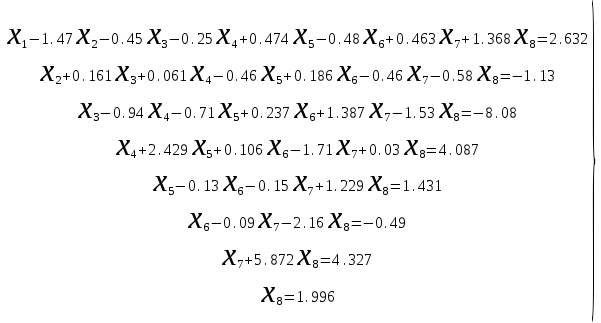 ,
, x 1 = -13,8731;
x 1 = -13,8731;