Задачи по кинематике. Решение Скорость равна первой производной от скорости по времени

• Название: Решение Скорость равна первой производной от скорости по времени
• Дата: 16.03.2022
• Размер: 89 Kb.
• Имя файла: Задачи по кинематике.doc
• Тип: Решение; #400625

Задача 1. Кинематика поступательного движения

Условие:

Точка движется поступательно по прямой так , что зависимость координаты от времени представляется уравнением х(t) = А + Вt +Сt2 + Dt3,м. Коэффициенты А = 2; В= - 20; С= 7; D = - 3.

Найдите:

1) уравнения скорости и ускорения;

2) значения координаты, скорости и ускорения к концу 3 секунды;

3) приращения координаты, скорости и ускорения за вторую секунду;

4) путь и перемещение пройденный точкой за 3 секунды.

Решение:

1. 
   Скорость равна первой производной от скорости по времени:
   

Ускорение равно первой производной от скорости по времени:

2. 
   Координата:
   

Скорость:


Ускорение:

3. 
   Приращение координаты за вторую секунду:
   

Приращение скорости за вторую секунду:

Приращение ускорения за вторую секунду:

4. 
   Перемещение пройденное точкой за три секунды:
   

м
Путь м

Задача 2. Кинематика вращательного движения

Условие:

Точка движется по окружности радиуса 0,2 м так, что зависимость пути от времени дается уравнением (рад).

Коэффициенты: А = 0,1; В = 0,4; С = 0,3; D = -0,15.

Найдите

1) уравнения: угловой скорости, углового ускорения, пути, проходимого точкой на ободе;

2) значения угловой скорости и углового ускорения через 2 сек от начала движения;

3) линейную скорость точки, тангенциальное, нормальное и полное ускорения точки через 2 с после начала движения;

4) значения угла поворота и пути, пройденного точкой за 2 сек от начала движения.

Решение:

1. 
   Угловая скорость равна первой производной от угла поворота:
   

Угловое ускорение равно первой производной от угловой скорости по времени:


Путь, который точка прошла на ободе, равен:

2. 
   Значение угловой скорости и углового ускорения через 2 секунды от начала движения: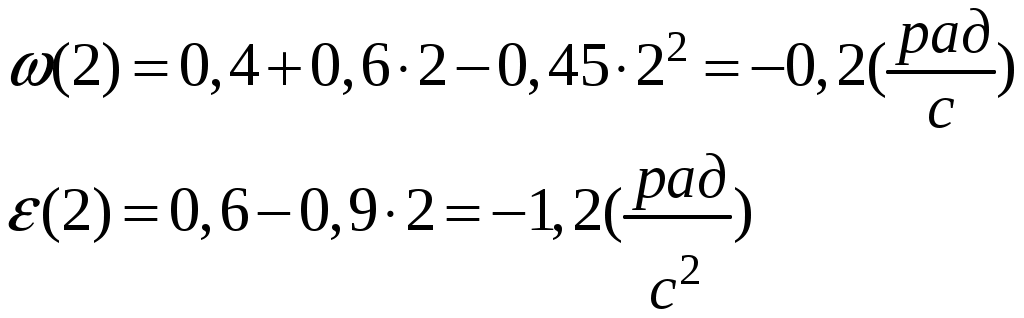
   

3. 
   Линейную скорость точки, тангенциальное, нормальное и полное ускорение точки через две секунды после начала движения:
   

Нормальное ускорение


Тангенциальное ускорение: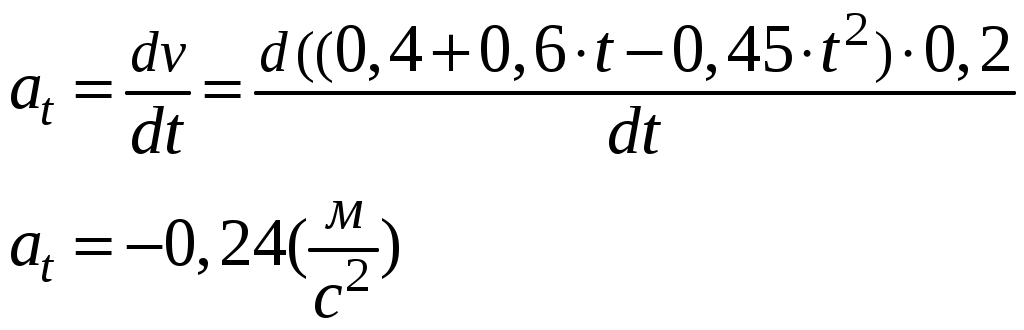


Полное ускорение:

4. 
   Значение угла поворота и пути, пройденного точкой за две секунды от начала: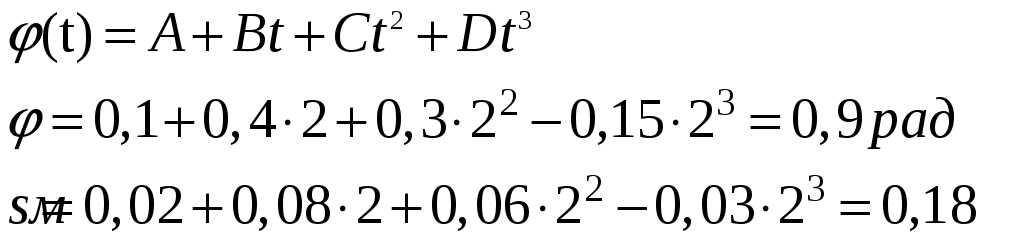