Решение слау методом Гаусса
 Скачать 224.5 Kb. Скачать 224.5 Kb.
|
|
Высшая математика Вопросы к экзамену Матрицы, виды матриц. Операции над матрицами и их свойства: сложение, умножение на число, произведение, возведение в целую неотрицательную степень, транспонирование. Понятие определителя. Вычисление определителей 1-3 порядков. Правило Саррюса. Вычисление определителей произвольного порядка n. Свойства определителей. Понятие минора, алгебраического дополнения. Вычисление определителей путем разложения определителей по элементам некоторой строки или некоторого столбца. Обратная матрица, методы ее вычисления. Ранг матрицы. Метод окаймляющих миноров для нахождения ранга матрицы. Метод присоединенной матрицы для вычисления обратной матрицы. Основные понятия: системы линейных алгебраических уравнений(СЛАУ), решение СЛАУ, совместная, несовместная, определенная, неопределенная СЛАУ, элементарные преобразования. Матричная форма СЛАУ. Критерий совместности СЛАУ. Теорема Кронекера – Капелли. Методы решения системы n линейных уравнений с n неизвестными. Метод Крамера. Метод обратной матрицы. Решение СЛАУ методом Гаусса. Однородные системы линейных уравнений. Структура общего решения однородной системы. Положение точки на прямой. Общее уравнение прямой на плоскости Уравнение прямой с угловым коэффициентом. Общее уравнение плоскости. Уравнение плоскости, перпендикулярной данному вектору и проходящей через данную точку. Параметрические и канонические уравнения прямой в пространстве. Прямая как линия пересечения двух плоскостей (общие уравнения прямой). Основные поверхности второго порядка: эллипсоид, гиперболоиды, параболоиды, цилиндры, вырожденные поверхности. Понятие множества и операции над множествами. Счётность множества. Функция (определение, основные свойства). Функция (определение, способы задания). Обратная функция, сложная функция. Основные элементарные функции и их графики. Числовая последовательность. Предел числовой последовательности. Предел функции в точке. Предел функции в бесконечности. Бесконечно большая и бесконечно малая функции. Основные теоремы о пределах. Первый замечательный предел. Второй замечательный предел. Непрерывность функций. Точки разрыва функции и их классификация. Основные теоремы о непрерывных функциях. Непрерывность элементарных функций. Производная функции (определение производной, ее физический и геометрический смысл). Производная суммы, разности, произведения и частного функций (доказательство теорем). Производная сложной функции. Производные основных элементарных функций. Дифференциал функции (понятие дифференциала функции, геометрический смысл дифференциала функции). Основные теоремы дифференциального исчисления. Возрастание и убывание функций (монотонность). Условия монотонности функций. Экстремум функции (максимум и минимум функций). Необходимое и достаточное условия экстремума. Схема исследования функций на экстремум. Выпуклость графика функции. Точки перегиба. Необходимое и достаточное условие перегиба. Схема исследования функций на выпуклость. Асимптоты графика функции (теоремы). Неопределенный интеграл. Табличные формулы нахождения неопределенного интеграла. Определённый интеграл и его свойства. Формула Ньютона Лейбница, её применения для вычисления определённого интеграла. Геометрические и механические приложения определённого интеграла. Понятие функции нескольких аргументов. Частные производные. Понятие дифференциального уравнения. Что понимается под частным и общим решениями дифференциального уравнения? При каких условиях задача Коши  имеет единственное решение. имеет единственное решение.Задачи и задания к экзамену  Задание 1. Решить систему уравнений: Задание 1. Решить систему уравнений:  Задание 2. Дать определение ранга матрицы. Ранг какой матрицы равен 0? Чему равен ранг матриц 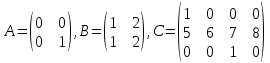 ? ?Задание 3. Найти обратную матрицу для матриц А и В, если это возможно:
Задание 4. Заданы вектора 1. Задание 5. Заданы вектора 1) скалярное произведение 2) косинус угла между векторами Задание 6. Заданы вектора 1) длину векторов 2) косинус угла между векторами если: 1. 2. 3. 4. 5. Задание 7. Дайте определение векторного произведения. Заданы векторы если: 1. 2. 3. 4. 5. Задание 8. Вычислить площадь треугольника с вершинами Задание 9. Вычислить определители третьего порядка:  ; ;  . .Задание 10. Вычислить определители:  ; ;  . .Задание 11. Найти обратную матрицу 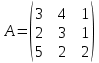 . .Задание 12. Решить по формулам Крамера систему уравнений:  . .Задание 14. Решить методом Гаусса и Жордана-Гаусса систему уравнений:  . .Задание 15. Найти вектор Задание 16. Найти угол, составленный единичными векторами Задание 17. Заданы векторы Задание 18. Вычислить площадь треугольника с вершинами Задание 19. В треугольнике с вершинами Задание 20. Определить тип, вычислить пределы:                 Задание 21. Что называется точкой разрыва функции? Как классифицируются точки разрыва? Какого рода разрывы имеют функции 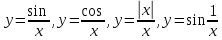 ? ?Задание 22. Сформулировать правило Лопиталя для раскрытия неопределенностей вида 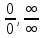 . Найти пределы используя правило Лопиталя: . Найти пределы используя правило Лопиталя:          Задание23. Сформулировать признак монотонности дифференцируемой функции на Задание23. Сформулировать признак монотонности дифференцируемой функции на    3) 3) Задание 24. Сформулировать достаточные условия экстремума непрерывной функции. Найти точки экстремума функции:      , ,   , 6) , 6)Задание 25. Какая кривая называется выпуклой вверх (вниз) на (а, в)? Что называется точкой перегиба кривой? Исследовать на выпуклость вниз (вверх) и найти точки перегиба графиков следующих функций:   Задание 26. Что называется асимптотой кривой? Какие асимптоты может иметь кривая? Найти асимптоты заданных кривых:      , 2) , 2) , 3) , 3) , 4) , 4)  , ,     , 6) , 6) , 7) , 7) . . Задание 27. На основании основных правил нахождения производных, найдите производную функции у(х) = 5х2 – 3х + 4. Задание 28. Дайте определение производной функции в точке. Найдите производную функции у(х) = х5-5х3+12х2- 140. Задание 29. Вычислить а) 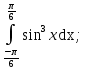 б) б) 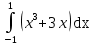 . .Задание 30. Вычислить: а) с точностью до 0,0001 определенный интеграл  ; ;б) с точностью до 0,0001 определенный интеграл  . .Задание 31. Найти область определения функции: а) Задание 32. Найти пределы:   Задание 33. Найти пределы, используя первый замечательный предел:          Задание 34. Найти пределы, используя второй замечательный предел: Задание 34. Найти пределы, используя второй замечательный предел:     Задание 35. Найти производных следующих функций1) Задание 35. Найти производных следующих функций1) 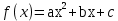 ; 2) ; 2) 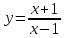 ; 4) ; 4)   Задание 36. Найдите мгновенную скорость движения тела в момент Задание 36. Найдите мгновенную скорость движения тела в момент Задание 37 . Исследовать на экстремум следующие функции:  1) 1) 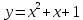 ; 2) ; 2) 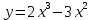 . 3) . 3) 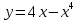 . .Задание 38. Найти точки перегиба функции и интервалы выпуклости (вогнутости) графиков следующих функций: 1) 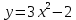 ; 2) ; 2) 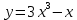 ; 3) ; 3) 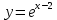 . . Задание 39. Найдите неопределенные интегралы: 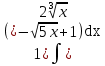 ; ; 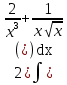 ; ; 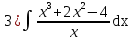 . . Задание 40. Вычислить:   1) 1) 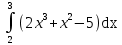 ; 2) ; 2) 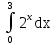 ; 3) ; 3)  . .Задание 41. Вычислите площадь фигуры, ограниченной линиями:                       Задание 42. Найти решение задачи Коши: Задание 43. Найти общее решение линейного дифференциального уравнения  Задание 44. Найти общее решение ДУ Задание 45. Найти общее решение линейного дифференциального уравнения  |


