Решение Согласно закону Архимеда на тело, погруженное в жидкость, действует выталкивающая сила, равная весу жидкости, вытесненной телом
 Скачать 0.86 Mb. Скачать 0.86 Mb.
|
|
Задача 4 Определить величину силы 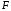 , необходимой для погружения малого сосуда диаметром , необходимой для погружения малого сосуда диаметром  мм на глубину мм на глубину 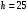 мм, в жидкости плотностью мм, в жидкости плотностью  кг/м3, заполняющую большой сосуд. Весом малого сосуда пренебречь. кг/м3, заполняющую большой сосуд. Весом малого сосуда пренебречь. Решение: Согласно закону Архимеда на тело, погруженное в жидкость, действует выталкивающая сила, равная весу жидкости, вытесненной телом:  Н. Н.Величина силы, необходимой для погружения малого сосуда, равна выталкивающей силе (силе Архимеда):  Н. Н.Задача 13 Вода из резервуара самотеком поступает в цех при температуре 40 оС по трубопроводу длиной  м. Уровень жидкости в резервуаре м. Уровень жидкости в резервуаре  м. Каким должно быть давление м. Каким должно быть давление 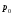 , чтобы обеспечивалась подача жидкости в количестве , чтобы обеспечивалась подача жидкости в количестве  л/с при л/с при  мм и манометрическом давлении в конце трубопровода мм и манометрическом давлении в конце трубопровода 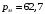 кПа. Значение абсолютной шероховатости кПа. Значение абсолютной шероховатости  мм. мм. Решение: Составим уравнение Бернулли для сечений 1-1 и 2-2 (свободная поверхность в резервуаре и место установки манометра) относительно оси сравнения 0-0 (ось трубопровода:  считая движение турбулентным принимаем коэффициент Кориолиса  и устанавливаем значения слагаемых, входящих в его левую и правую часть: и устанавливаем значения слагаемых, входящих в его левую и правую часть: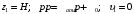 ; ; . .Потери напора на трение: 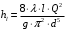 , ,где  – коэффициент гидравлического трения. – коэффициент гидравлического трения.Тогда уравнение Бернулли примет вид:  , ,то есть получено выражение, в котором неизвестны два параметра: коэффициент гидравлического трения 𝜆 и диаметр трубопровода. Выразим неизвестные величины через расход Q. Число Рейнольдса:  ; ;Коэффициент гидравлического трения: 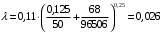 . .Тогда   Па. Па.Задача 22 Два одинаковых центробежных насоса, включены параллельно и подают воду в магистральный трубопровод CD, длина которого 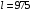 м, коэффициент гидравлического трения м, коэффициент гидравлического трения 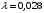 , диаметр , диаметр 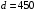 мм, трубопроводы насосов до точки С имеют одинаковые длины мм, трубопроводы насосов до точки С имеют одинаковые длины  м и м и 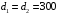 мм, коэффициент гидравлического трения мм, коэффициент гидравлического трения 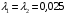 . Учитывая только потери напора по длине, определить подачу, напор и мощность на валу насосов. . Учитывая только потери напора по длине, определить подачу, напор и мощность на валу насосов.
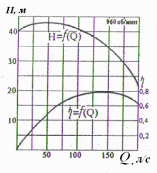
Решение: Уравнение характеристики сети - зависимость потребного напора от расхода:  ; ;  Для решения задачи определяем положение рабочей точки – точки пересечения главной характеристики насоса (при условии работы двух одинаковых центробежных насоса, включенных параллельно), т.е. 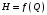 и характеристики сети и характеристики сети  . Точки для построения характеристики сети по уравнению, представлены в таблице 1. . Точки для построения характеристики сети по уравнению, представлены в таблице 1.Таблица 1
 Для рабочей точки расход составляет 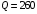 л/с, напор л/с, напор 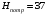 м, КПД м, КПД 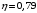 . .Полезная мощность одного насоса составляет: 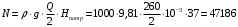 Вт. Вт. |


 , м
, м