Пример решения РГР-2. Решение Составляем расчетную схему стержня с указанием приложенных нагрузок и линейных размеров в масштабе (рисунок 2)

• Название: Решение Составляем расчетную схему стержня с указанием приложенных нагрузок и линейных размеров в масштабе (рисунок 2)
• Дата: 25.11.2020
• Размер: 217.45 Kb.
• Имя файла: Пример решения РГР-2.docx
• Тип: Решение; #153585

Министерство науки и высшего образования Российской Федерации

Филиал федерального государственного бюджетного образовательного учреждения

высшего образования

“Уфимский государственный нефтяной технический университет” в г. Салавате

(Филиал ФГБОУ ВОУГНТУ в г. Салавате)
Кафедра “Оборудование предприятий нефтехимии и нефтепереработки”
ПОСТРОЕНИЕ ЭПЮР ВНУТРЕННИХ СИЛОВЫХ ФАКТОРОВ

Расчетно-графическаяая работа № 2

по дисциплине “Прикладная механика”
ОПНН-18.03.01-02.02.28 РГР

Выполнил:

студент гр. БТПз-19-21 В.А. Михайлов

(Подпись, дата)
Проверил:

канд. техн. наук, доцент Р.Р. Газиев

(Подпись, дата)
Нормоконтроль:

канд. техн. наук, доцент Р.Р. Газиев

(Подпись, дата)
Салават

2020

Задача 1 - Построение эпюры продольной силы
Исходные данные: q = 700 кН/м; а₁ = 0,7 м;

а₂ = 0,65 м; а₃ = 0,6 м; F₂ = 2qa, F₃ = qa;

F₂ = 2·700·0,6 = 840 кН; F₃ = 700·0,6 = 420 кН.

Заданная схема стержня представлена на рисунке 1.1.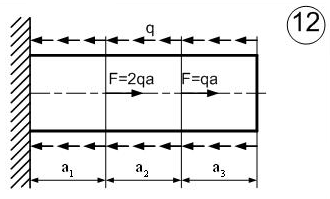



Рисунок 1.1 – Заданная схема стержня

Решение

Составляем расчетную схему стержня с указанием приложенных нагрузок и линейных размеров в масштабе (рисунок 1.2).

Разбиваем стержень на 3 силовых участка, применяем метод сечения.

Рассмотрим участок I (АВ):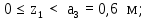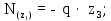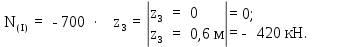







Рассмотрим участок II (ВС):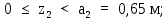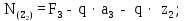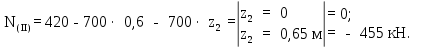







Рассмотрим участок III (СD):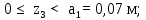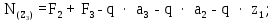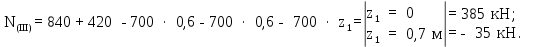







По полученным значениям построим расчётную схему стержня (рисунок 1.2).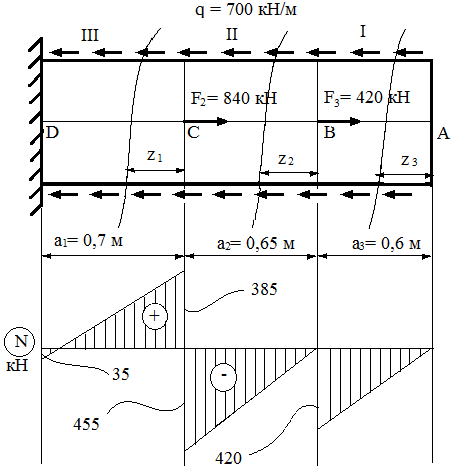

Рисунок 1.2 – Расчетная схема стержня

Задача 2 - Построение эпюры крутящего момента
Исходные данные: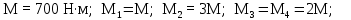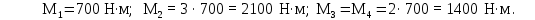



Заданная схема вала представлена на рисунке 2.1.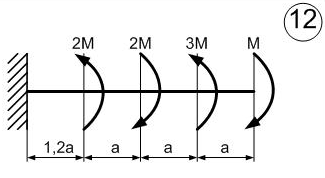


Рисунок 2.1 – Заданная схема вала

Решение

Разбиваем вал на четыре силовых участка AB, BC, CD и DE (рисунок 2.2). Для каждого участка применяем метод сечений, составляем уравнения крутящего момента, по которым определяем характерные ординаты.

Рассмотрим участок I (АВ):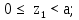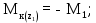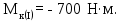







Рассмотрим участок II (ВC):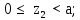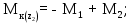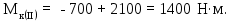







Рассмотрим участок III (CD):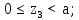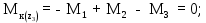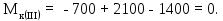







Рассмотрим участок IV (DE):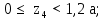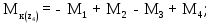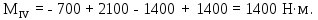







По полученным значениям построим эпюру крутящего момента (рисунок 2.2).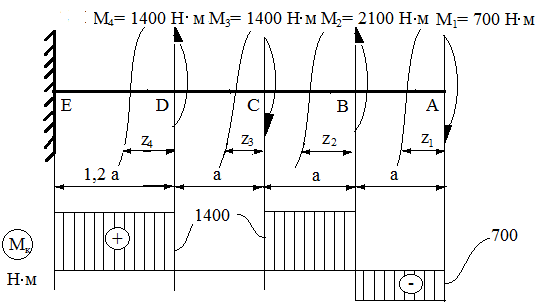


Рисунок 2.2 – Расчетная схема вала

Задача 4 - Построение эпюры поперечной силы и изгибающего момента для простой балки
Исходные данные: M = mqa²; m = 1,2; M = 1,2 qa².

Заданная схема простой балки представлена на рисунке 4.1.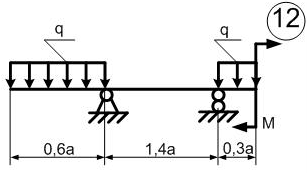


Рисунок 4.1 – Заданная схема простой балки
Решение

Составим расчётную схему балки (рисунок 4.2)

Определяем опорные реакции балки. Направим реакции опор в точке C и в точке B.

Составим уравнение проекции сил на ось z:

Н_B + 0 = 0;

Н_B = 0.

Составим уравнение моментов относительно опоры C: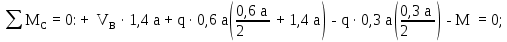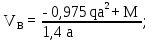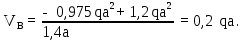





Составим уравнение моментов относительно опоры B: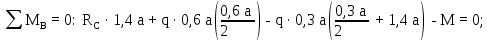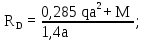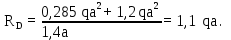





Для проверки составим уравнение проекций всех сил на ось y: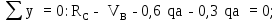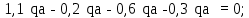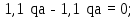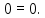









Условие проверки выполняется, значит, проведенные выше вычисления реакций опор верны.

Разбиваем балку на три силовых участка AB, BC и CD (рисунок 3.2), для каждого участка применяем метод сечений и составляем уравнения поперечной силы и изгибающего момента. Определяем характерные ординаты поперечной силы и изгибающего момента.

Рассмотрим участок I (АВ):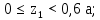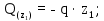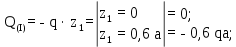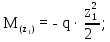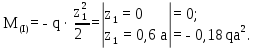











Рассмотрим участок II (BC):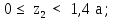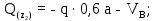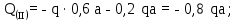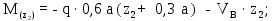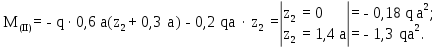











Рассмотрим участок III (DC):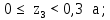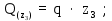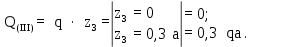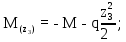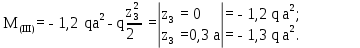











По полученным значениям построим эпюру поперечной силы и изгибающего момента (рисунок 4.2).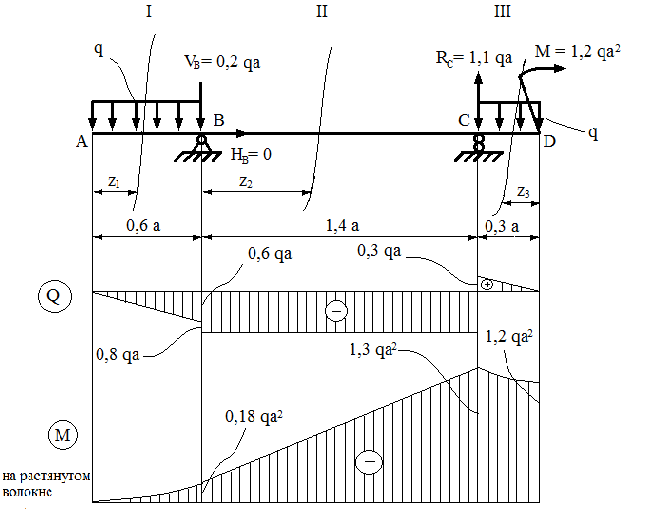



Рисунок 4.2 – Расчетная схема простой балки