Решение дробно рациональных уравнений. Решение дробно-рациональных уравнений. Решение состоит из следующих этапов Надо перенести все слагаемые в левую часть уравнения, для того чтобы справа был ноль
 Скачать 2.42 Mb. Скачать 2.42 Mb.
|
|
Решение дробно-рациональных уравнений Рациональные уравнения - это уравнения содержащие рациональные алгебраические дроби. Их решение состоит из следующих этапов: 1. Надо перенести все слагаемые в левую часть уравнения, для того чтобы справа был ноль. 2. Надо сложить все алгебраические дроби в левой части уравнения. Для этого необходимо привести все дроби к общему знаменателю. Если есть недробные выражения, тогда принимаем их знаменатель за единицу. Для того, чтобы привести дроби к общему знаменателю, лучше разложить знаменатели на множители. Для разложения на множители можно применять следующие методы: а. Вынесение общего множителя за скобки. б. Метод группировки. в. Формулы сокращенного умножения. г. Разложение на множители с использованием формулы  , ,где 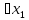 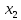 – решения квадратного уравнения – решения квадратного уравнения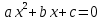 3. После того, как дроби в левой части уравнения приведены к общему знаменателю и сложены (вычтены), В левой части уравнения получается одна дробь, которую надо упростить. Для этого необходимо раскрыть скобки в числителе и привести подобные слагаемые. 4. Итак в левой части уравнения должна получиться алгебраическая дробь, а справа ноль. Вспомним, что дробь равна нули, если ее числитель равен нулю, а знаменатель не равен нулю. Приравниваем к нулю числитель дроби. Решаем получившиеся уравнение, полученные решения по-очереди подставляем в знаменатель, если знаменатель обращается в ноль, отбрасываем такое решение, как ложное. Пример 1 Решим дробно-рациональное уравнение: 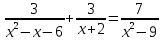 Переносим слагаемое 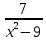 в левую часть уравнения в левую часть уравнения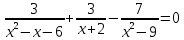 Раскладываем на множители выражения в знаменателях. Для начала посмотрим, как раскладывается на множители выражение в знаменателе первой дроби 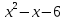 будем использовать формулу  . Решим квадратное уравнение . Решим квадратное уравнение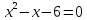 его решения 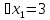 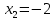 . Разложим на множители выражение . Разложим на множители выражение 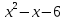 , используя формулу , используя формулу  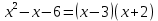 Знаменатель третьей дроби 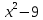 раскладывается на множители по формуле разности квадратов раскладывается на множители по формуле разности квадратов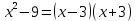 Наше уравнение тогда примет вид 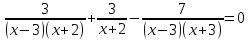 Для приведения дробей к общему знаменателю, домножим числитель и знаменатель первой дроби на (x+3), второй дроби на (x-3)(x+3), третьей дроби на (x+2). Получим 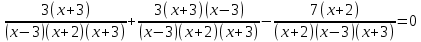 Теперь все три дроби имеют одинаковый (общий) знаменатель. Складываем их. Внимание! Пока выражения не записаны под общей чертой, ни в коем случае не раскрываем скобки! Это мощнейший генератор ошибок. НЕ НАДО ЭТОГО ДЕЛАТЬ! 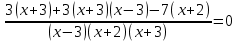 Затем надо упростить выражение в числителе. Вот теперь можно (и нужно) раскрыть скобки в числителе 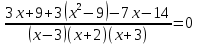 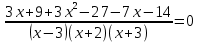 Необходимо отметить, что в знаменателе скобки раскрывать не надо. Это бесполезная, более того вредная работа. Если раскрыть скобки в знаменателе, то это создаст проблемы в дальнейшем. Приводим подобные слагаемые в числителе 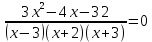 Приравниваем к нулю числитель дроби 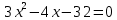 Решаем это квадратное уравнение 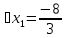 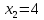 . .Теперь надо проверить, не является ли какое-нибудь решение ложным. Для этого подставим их по-очереди в знаменатель Подставим 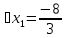 вместо x вместо x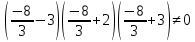 Знаменатель не равен нулю. Значит решение истинное. Подставим 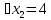 вместо x вместо x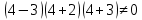 Знаменатель не равен нулю. Значит это решение истинное тоже истинное. Ответ: 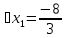 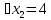 Примечание. Обратим внимание, как легко понять, что выражение в знаменателе не равно нули. Для этого необходимо, всего лишь, чтобы каждый множитель был не равен нулю. Если бы мы переусердсвовали, и раскрыли скобки в знаменателе, то получили бы следующие проблемы 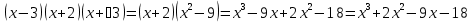 Попробуем подставить в выражение 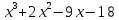 первое решение уравнения первое решение уравнения 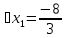 (чтобы проверить его на истинность) (чтобы проверить его на истинность) 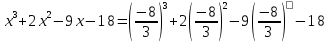 Попробуй-ка посчитай теперь, равно это выражение нулю или нет! Что не нравится? Не надо было скобки раскрывать в знаменателе! Пример 2 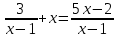 Переносим все влево 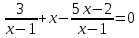 У слагаемых без знаменателя записываем знаменатель 1 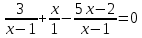 Приводим к общему знаменателю 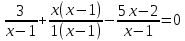 Складываем дроби 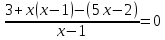 Раскрываем скобки в числителе 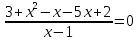 Приводим подобные слагаемые 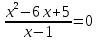 Приравниваем к нулю числитель 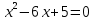 Решаем получившееся уравнение 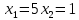 Проверим, нет ли среди полученных решений ложных. Проверим первое решение 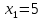 , подставим 5 вместо x в знаменатель дроби , подставим 5 вместо x в знаменатель дроби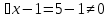 Все в порядке. При x=5 знаменатель не равен нулю, следовательно решение 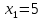 истинное. истинное.Проверим теперь второе решение 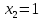 , подставим 1 вместо x в знаменатель дроби , подставим 1 вместо x в знаменатель дроби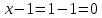 Бац! При x=0, знаменатель дроби обращается в ноль. На ноль делить нельзя. Значит решение 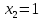 является ложным. Ответ: является ложным. Ответ: 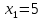 . . |
