задачи термодинамика. Задачи термодинамика. Решение Состояние исследуемой газовой смеси описывается уравнением Менделеева Клайперона Применительно ко всему объему эти уравнения принимают вид
 Скачать 0.84 Mb. Скачать 0.84 Mb.
|
|
. Смесь идеальных газов задана объемными долями: rCO2 0,2, rN2 0,6, rO2 0,2. Общая масса смеси m 10 кг. Объем смеси в начальном состоянии V1 4 м3 , температура t1 387˚C. В результате адиабатного расширения смеси ее давление уменьшается до значения p20,1 МПа. Определить давление смеси в начальном состоянии, температуру и объем смеси в конечном состоянии, работу расширения и изменение внутренней энергии смеси. Считать, что теплоемкость газов не зависит от температуры и определяется по табл. 1. Определить парциальные давления газов, входящих в смесь, в конечном состоянии. Изобразить процесс в p - и Ts - диаграммах. Решение Состояние исследуемой газовой смеси описывается уравнением Менделеева – Клайперона: 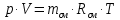 Применительно ко всему объему эти уравнения принимают вид: Из структуры уравнение Менделеева-Клайперона следует, что, в начале необходимо определить газовую постоянную смеси Rсм. 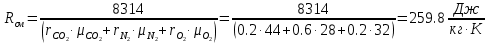 Определим массовые доли компонентов смеси: 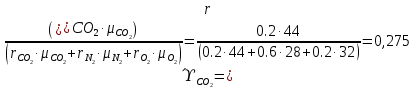 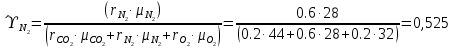 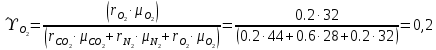 Для анализа процесса сжатия смеси необходимо найти показатель адиабаты k, для нахождения значения которого нужно рассчитать изобарную сpсм и изохорную сvсм теплоемкости смеси, по таблице определим значения мольных теплоёмкостей компонентов. 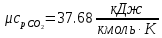 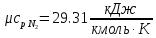 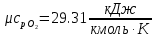 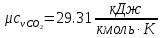 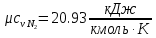 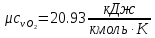 Переводим значения мольных теплоемкостей в массовые: 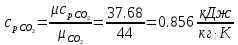 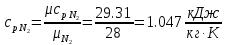 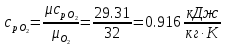 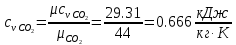 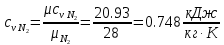 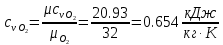 По найденным массовым долям компонентов и их теплоёмкостям найдем теплоёмкости смеси: 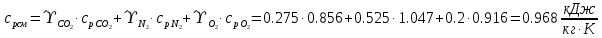 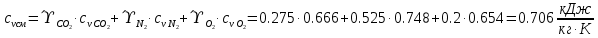 Определим значение показателя адиабаты: 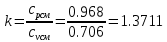 Определим начальное давление: 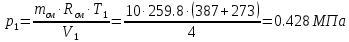 Далее определим конечный объем смеси: 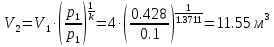 Рассчитаем конечную температуру смеси: 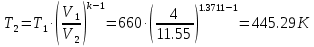 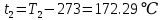 Найдём удельную работу расширения газовой смеси: 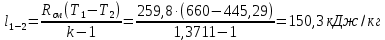 Применительно ко всей смеси работа расширения равна: 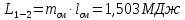 Определим изменение внутренней энергии: 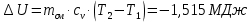 Определим парциальные давления компонентов газовой смеси: 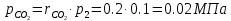 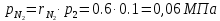 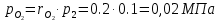 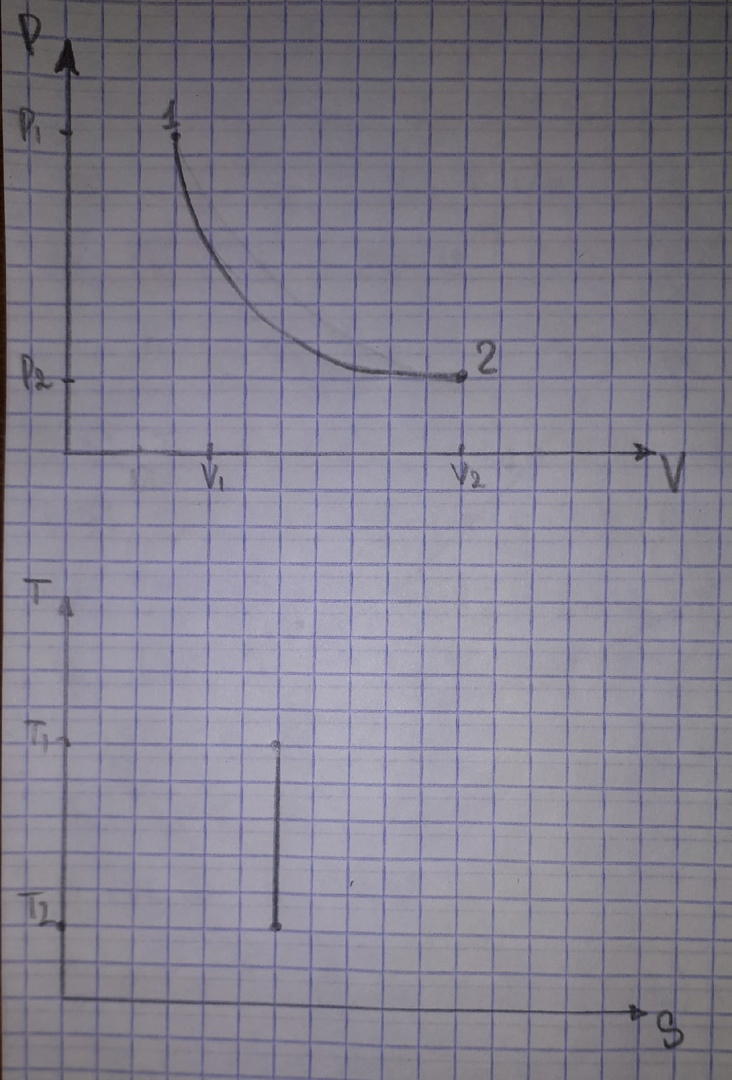 Рисунок 1 – Цикл в P-V и T-S координатах 13. Воздух из начального состояния 1 изотермически сжимается до состояния 2, а затем в изобарном процессе расширяется до состояния 3, в котором 3 1 . Параметры воздуха в точке 2 p2 0,5 МПа и t2 200˚C. Температура воздуха в точке 3 t3 1400 ˚C. Показать процесс 1-2-3 в p - и Ts - диаграммах. Определить значения t, p и воздуха в точках 1, 2 и 3. Вычислить удельные значения работы, теплоты, изменения внутренней энергии и энтропии воздуха в процессах 1-2, 2-3 и 1-2-3 в целом. Изобарный процесс рассчитать с учетом зависимости теплоемкости воздуха от температуры (см. табл. 2). Решение Определим значение удельного объема в точке 2: 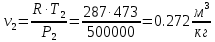 Определим параметры в точке 1, для этого найдем значение объема в точке 3: 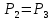 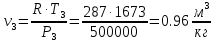 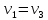 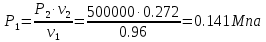 Из условия: 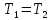 Когда параметры во всех точках определены, найдем удельные значения работы, теплоты, изменения внутренней энергии и энтропии воздуха. Процесс 1-2: Удельная работа: 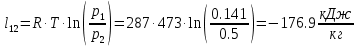 Теплота: 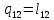 Изменение внутренней энергии: 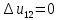 Изменение энтропии: 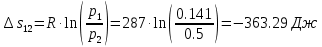 Процесс 2-3: Удельная работа: 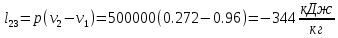 Теплота: 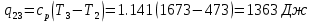 Изменение внутренней энергии: 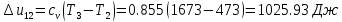 Изменение энтропии: 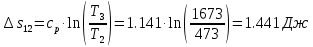 Работа цикла: 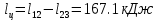 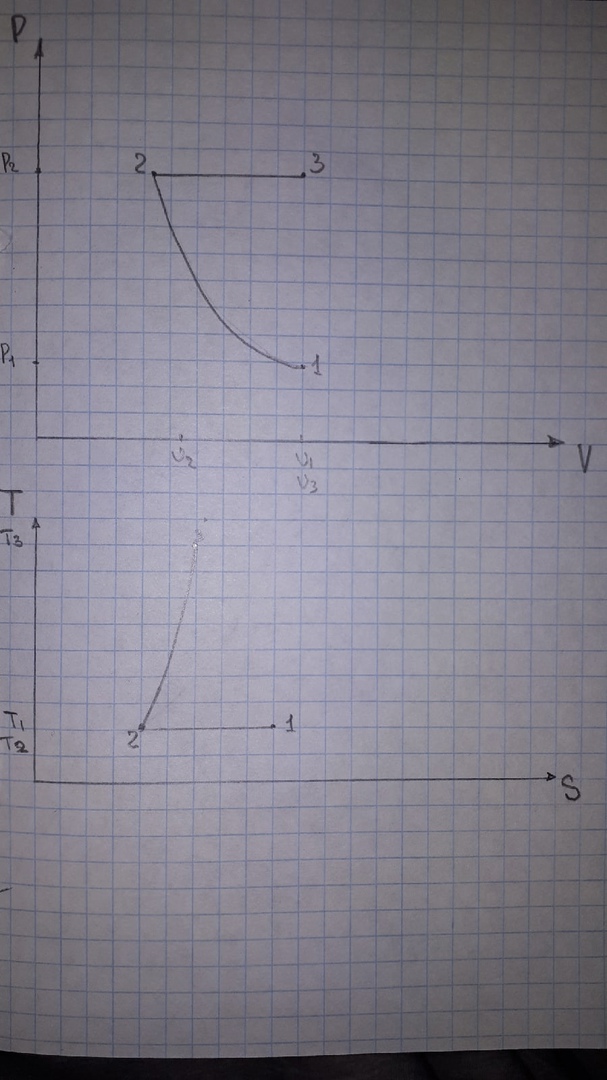 Рисунок 2 - Цикл в PV и TS координатах 29. Определить массовую и объемную (при начальных условиях) подачу двухступенчатого компрессора, в котором адиабатно сжимается воздух от давления p10,1 МПа (t1 20 C) до p22,2 МПа. Теоретическое значение мощности, затрачиваемой на привод компрессора, N100 кВт. Определить также количество теплоты, которое отводится от воздуха в промежуточном холодильнике. Изобразить процессы в p - и Ts - диаграммах. Решение Из формулы мощности при адиабатном сжатии определим объёмную подачу: 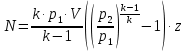 Где показатель адиабаты k=1.4, количество ступеней z=2 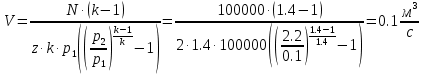 Найдем массовую подачу: 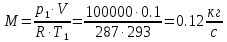 Так как процесс адиабатный отводимая теплота: 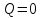 Определим значение объема в точке 1: 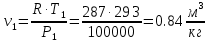 Определи температуру и объем в точке 2: 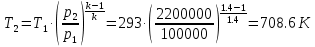 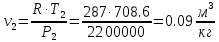 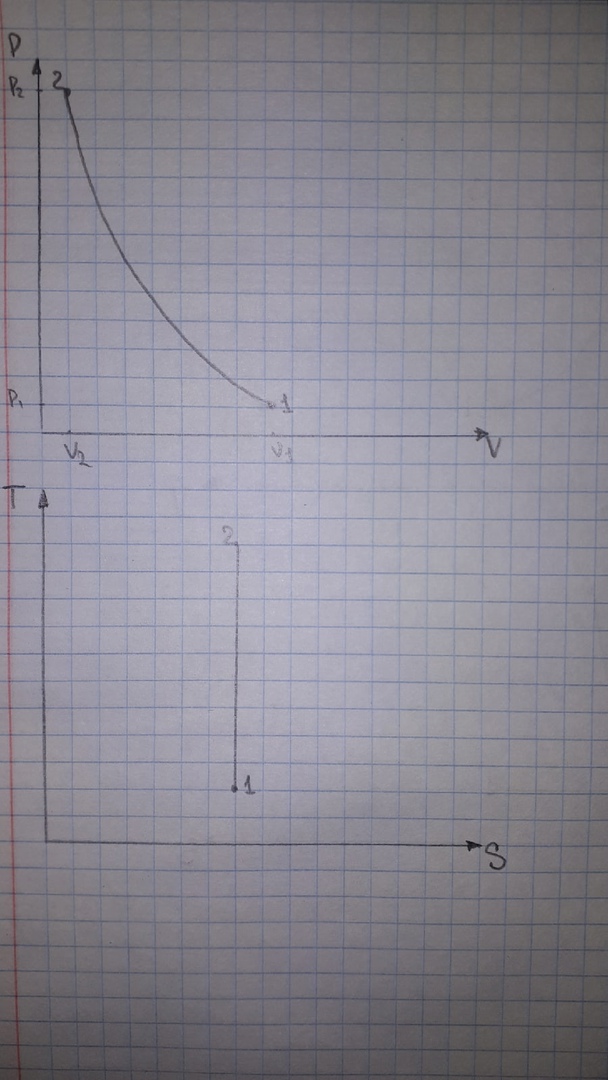 Рисунок 3 - Цикл в PV и TS координатах 39. Рассчитать цикл ГТУ с адиабатным сжатием в компрессоре, изобарным подводом теплоты и предельной регенерацией, если начальные параметры рабочего тела p10,1 МПа, t10˚C, температура воздуха на выходе из компрессора t2200˚C, температура рабочего тела на выходе из турбины t4450˚C. Определить параметры в характерных точках цикла, поведенное и отведенное количество теплоты, полезную работу и термический КПД цикла, а также термический КПД цикла Карно в том же интервале температур. Изобразить цикл в координатах p, и T,s . Рабочее тело – воздух. Решение Определим параметры в характерных точках: Точка 1: 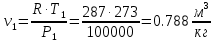 Точка 2: Определим давление по уравнению адиабаты: 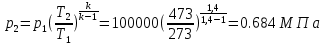 Определим объем: 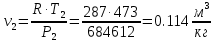 Точка 3: 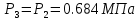 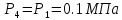 Определим температуру по уравнению адиабаты: 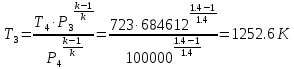 Определим объем: 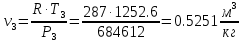 Точка 4: Определим объем: 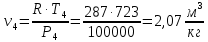 Определим подведённое количество теплоты с учетом предельной регенерации: 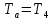 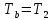 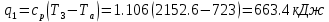 Отведенное количество теплоты: 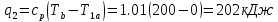 Работа цикла: 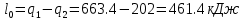 Термический КПД цикла: 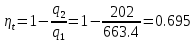 Термический КПД цикла Карно в том же интервале температур: 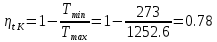 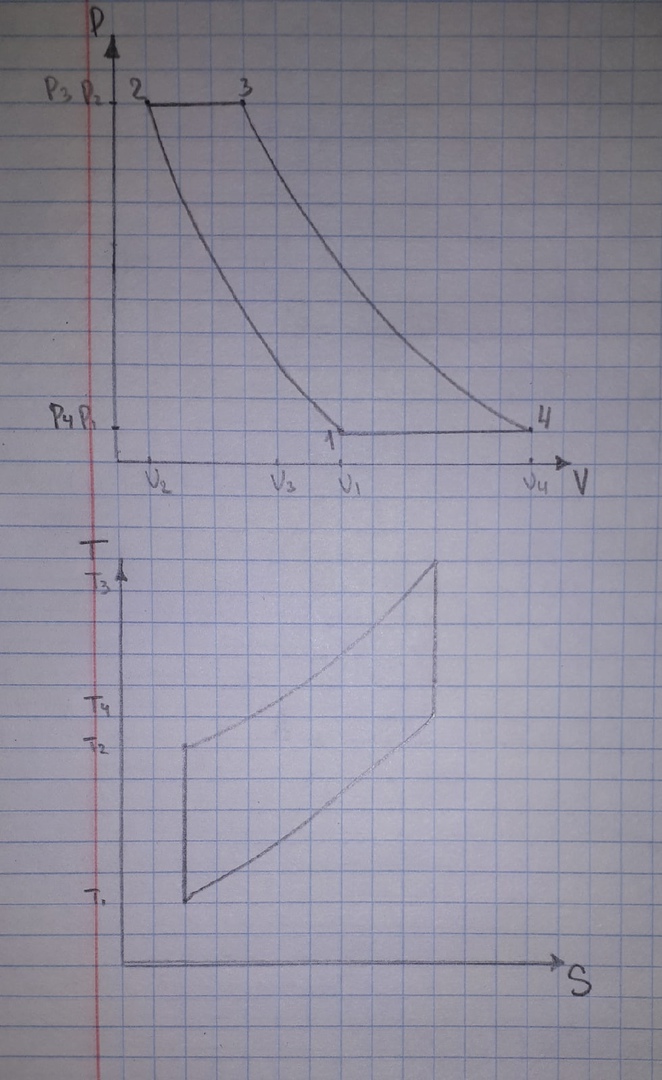 Рисунок 4 - Цикл в PV и TS координатах |
