На основе эскиза, представленного в Приложении 1, построить CAD-модель изделия, а также создать ассоциативный чертеж данного изд. записка. Решение. Строим в масштабе план механизма в указанном положении. Длина звена ав l a в
 Скачать 198.02 Kb. Скачать 198.02 Kb.
|
|
2. Графическое исследование кинематики плоских рычажных механизмов II класса Задание 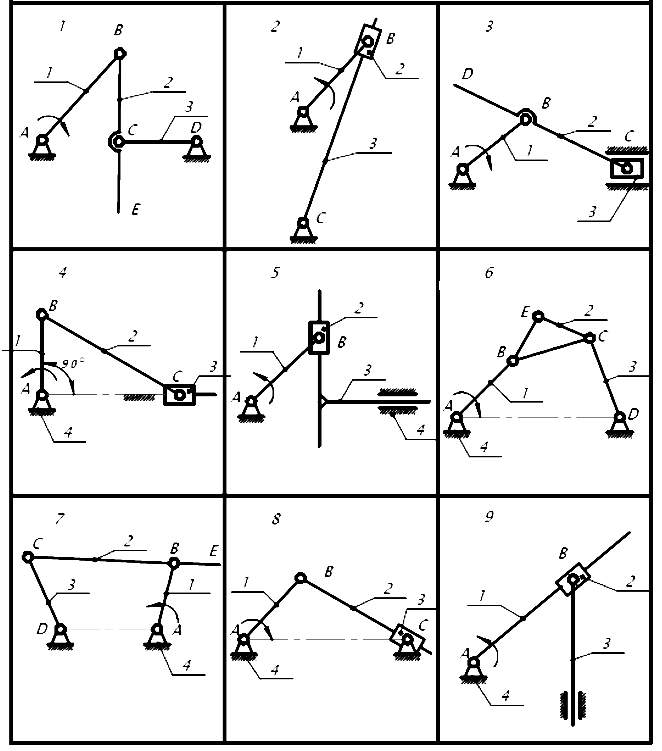 Рис. 2.1 Решение. 1. Строим в масштабе план механизма в указанном положении. Длина звена АВ - LAВ=0,4 м. Определяем масштабный коэффициент: 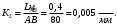 Определяем размеры остальных звеньев: 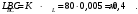 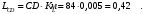 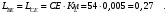 2. Строим план скоростей. Определяем скорость точки В. 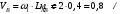 Вектор скорости 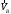 перпендикулярен кривошипу АВ. перпендикулярен кривошипу АВ.Зададим длину отрезка, изображающего вектор скорости 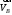 на плане: на плане: 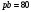 мм. мм.Найдём масштаб плана скоростей: 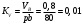 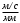 Из полюса плана скоростей 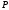 откладываем данный отрезок в направлении, перпендикулярном АВ в направлении угловой скорости откладываем данный отрезок в направлении, перпендикулярном АВ в направлении угловой скорости 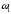 . .Определяем скорость точки С. Запишем векторное уравнение: 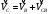 . .Уравнение решаем графически. Направления векторов скоростей: 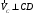 , , 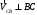 . .Продолжим строить план скоростей, используя правило сложения векторов. Из конца вектора 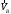 (точка (точка 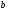 ) проводим направление вектора ) проводим направление вектора 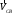 . Из полюса (точка . Из полюса (точка 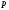 ) проводим направление вектора ) проводим направление вектора 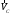 . На пересечении двух проведённых направлений получим точку . На пересечении двух проведённых направлений получим точку  . Измеряя длины полученных отрезков и умножая их на масштаб . Измеряя длины полученных отрезков и умножая их на масштаб 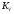 , получим значения скоростей: , получим значения скоростей: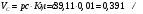 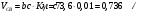 Определяем скорость точки Е. Воспользуемся следствием из теоремы подобия. Составим пропорции: 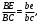 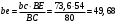 мм мм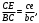 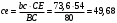 мм ммТочку е находим на пересечении окружностей радиусом 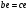 , проведенных из точек b и c. , проведенных из точек b и c. Величина скорости точки E: 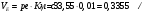  Определение угловой скорости шатуна BC. 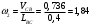 с-1 с-1Для определения направления 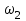 переносим вектор переносим вектор 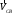 в точку C шатуна BC и смотрим как она движется относительно точки B. Направление этого движения соответствует в точку C шатуна BC и смотрим как она движется относительно точки B. Направление этого движения соответствует  . В данном случае угловая скорость . В данном случае угловая скорость 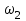 направлена против часовой стрелки. направлена против часовой стрелки.Определение угловой скорости коромысла CD. 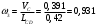 с-1 с-1Для определения направления 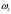 переносим вектор переносим вектор 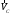 в точку C коромысла CD и смотрим как она движется относительно точки D. Направление этого движения соответствует в точку C коромысла CD и смотрим как она движется относительно точки D. Направление этого движения соответствует 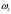 . В данном случае угловая скорость . В данном случае угловая скорость 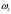 направлена по часовой стрелке. направлена по часовой стрелке.3. На отдельном листе строим плана механизма в том же масштабе и строим план ускорений. Определяем ускорение точки В. 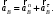 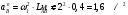 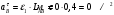 Вектор ускорения 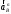 направлен параллельно кривошипу АВ от точки В к точке А. направлен параллельно кривошипу АВ от точки В к точке А. Зададим длину отрезка, изображающего вектор ускорения 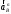 на плане: на плане: 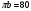 мм. мм.Найдём масштаб плана ускорений: 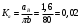 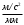 . .Из полюса плана ускорений  откладываем данный отрезок в направлении, параллельном АВ от точки В к точке А. откладываем данный отрезок в направлении, параллельном АВ от точки В к точке А.Определяем ускорение точки С. Запишем систему векторных уравнений: 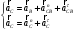 . .Уравнение решаем графически. Нормальные ускорения равны: 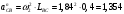 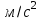 . .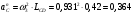 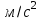 . .Найдём отрезки, изображающие векторы ускорений на плане: 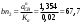 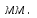 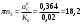 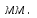 Продолжаем строить план ускорений, используя правило сложения векторов. Вектор ускорения 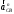 направлен параллельно ВС. Откладываем отрезок направлен параллельно ВС. Откладываем отрезок 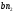 из точки из точки 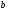 плана ускорений в указанном направлении от точки С к точке В. плана ускорений в указанном направлении от точки С к точке В. Вектор ускорения 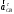 направлен перпендикулярно ВС. Проводим это направление из точки направлен перпендикулярно ВС. Проводим это направление из точки 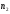 плана ускорений. Вектор ускорения плана ускорений. Вектор ускорения 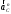 направлен параллельно CD. Проводим это направление из полюса от точки C к точке D. Вектор ускорения направлен параллельно CD. Проводим это направление из полюса от точки C к точке D. Вектор ускорения 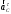 направлен перпендикулярно CD. Проводим это направление из точки направлен перпендикулярно CD. Проводим это направление из точки 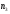 плана ускорений. Две прямые линии, проведённые из точек плана ускорений. Две прямые линии, проведённые из точек 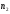 и и 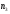 в указанных направлениях, пересекаются в точке в указанных направлениях, пересекаются в точке  . . Найдем величины ускорений. Измеряя длины полученных отрезков и умножая их на масштаб 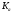 , получим: , получим: 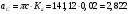 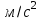 . .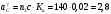 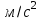 . .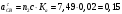 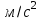 . .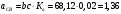 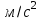 . .Определение ускорения точки E. Воспользуемся следствием из теоремы подобия. Составим пропорции: 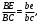 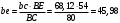 мм мм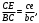 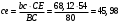 мм ммТочку е находим на пересечении окружностей радиусом 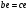 , проведенных из точек b и c. , проведенных из точек b и c. Величина ускорения точки E: 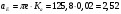 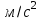 . . Определение углового ускорения шатуна BC. 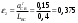 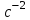 . .Определение углового ускорения коромысла CD. 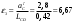 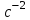 . .Показываем на плане механизма направление угловых ускорений в сторону соответствующих им тангенциальных ускорений 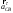 и и  , соответственно. , соответственно. |
