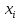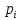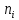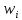решение задач по теории вероятности. Решение Т. к сумма вероятностей дискретной случайной величины равна 1, то верно равенство
 Скачать 77.27 Kb. Скачать 77.27 Kb.
|
|
Вариант 27 2. Дискретная случайная величина задана законом распределения 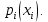 Найти величину Найти величину 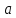 , построить график функции распределения данной случайной величины. Вычислить математическое ожидание, дисперсию и среднее квадратическое отклонение данной случайной величины. , построить график функции распределения данной случайной величины. Вычислить математическое ожидание, дисперсию и среднее квадратическое отклонение данной случайной величины.
Решение: Т.к. сумма вероятностей дискретной случайной величины равна 1, то верно равенство: 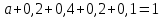 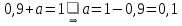 Тогда закон распределения имеет вид:
Найдем функцию распределения и построим ее график; 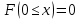 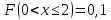 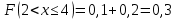 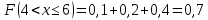 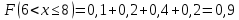 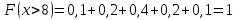 Функция распределения: 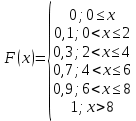 График функции распределения: 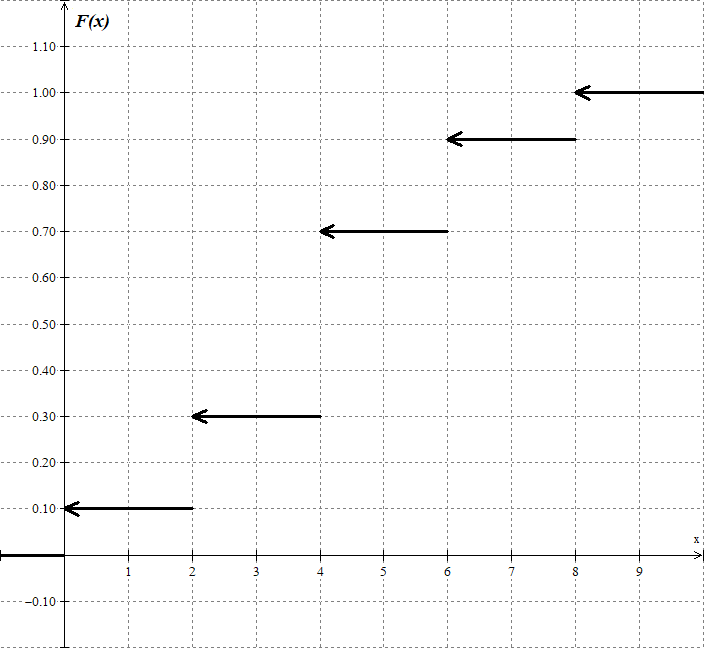 Математическое ожидание дискретной случайной величины определяем по формуле: 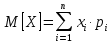 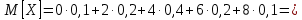 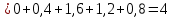 Дисперсиюопределяем по формуле: 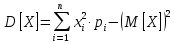 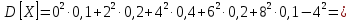 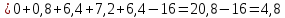 Среднее квадратическое отклонение вычисляем по формуле: 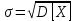 Тогда: 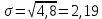 3. Плотность распределения вероятностей непрерывной случайной величины задана выражением: 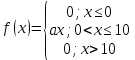 Найти величину коэффициента 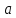 , написать аналитическое выражение и построить график функции распределения, найти математическое ожидание, дисперсию и среднее квадратическое отклонение данной случайной величины. Найти вероятности попадания данной случайной величины в интервалы , написать аналитическое выражение и построить график функции распределения, найти математическое ожидание, дисперсию и среднее квадратическое отклонение данной случайной величины. Найти вероятности попадания данной случайной величины в интервалы 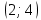 и и 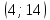 . .Решение: Коэффициент 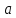 можно определить из условия: можно определить из условия: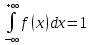 В нашем случае: 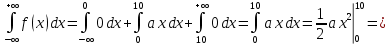 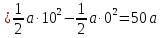 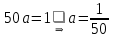 Тогда: 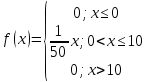 Функцию распределения найдем из соотношения: 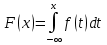 При 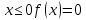 : :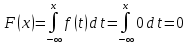 При 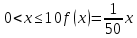 : :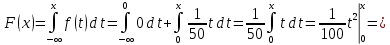 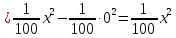 При 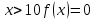 : :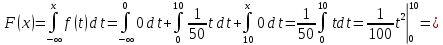 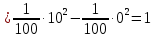 Тогда функция распределения: 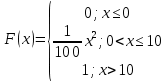 График функции распределения 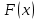 : :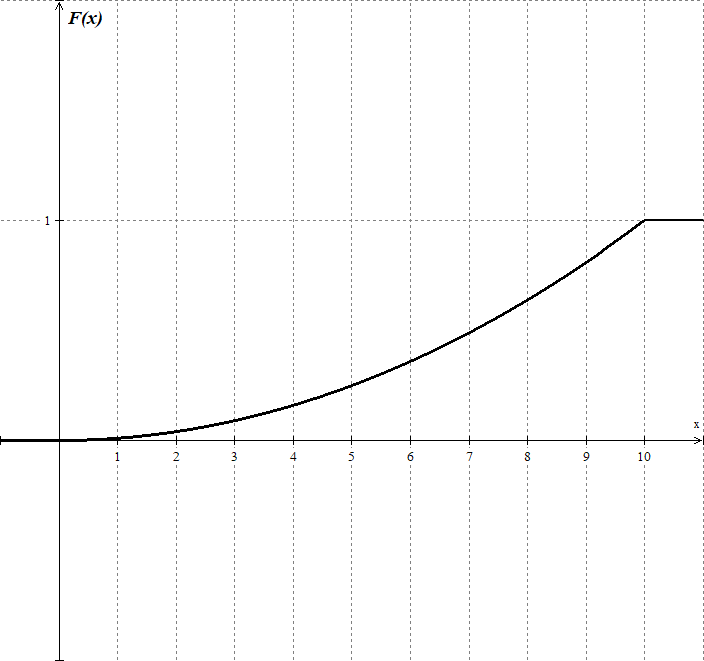 График плотности распределения  : : Найдем математическое ожидание 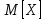 , дисперсию , дисперсию 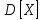 и среднее квадратическое отклонение и среднее квадратическое отклонение 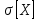 : :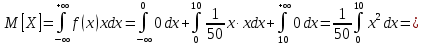 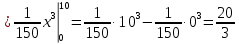 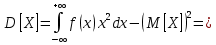 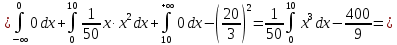 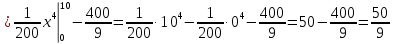 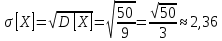 Найдем вероятность попадания случайной величины 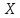 в интервал в интервал 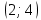 : :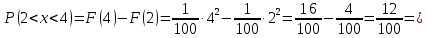 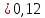 Найдем вероятность попадания случайной величины 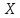 в интервал в интервал 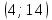 : :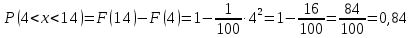 4. Дана нормально распределенная случайная величина с математическим ожиданием 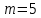 и дисперсией и дисперсией 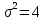 . Найти вероятность попадания данной случайной величины в интервал . Найти вероятность попадания данной случайной величины в интервал 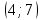 . . Решение: Для нормально распределенной случайной величины: 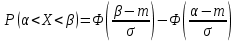 Тогда в нашем случае: 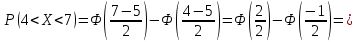 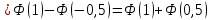 По таблице значений функции 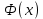 найдем: найдем: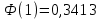 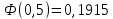 Тогда: 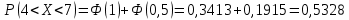 5. Дискретная случайная величина задана выборкой: 1, 2, 3, 3, 3, 3, 3, 1, 1, 1, 2, 3, 3, 1, 1, 1, 1, 3, 3, 1, 1, 1, 2, 3, 1. Построить полигон частот и эмпирическую функцию распределения. Найти выборочное среднее и выборочную дисперсию. Решение: Построим вариационный ряд, т.е. упорядочим выборку по возрастанию: 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3. В заданной выборке объем 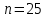 , дискретная случайная величина , дискретная случайная величина 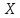 принимает три различных значения: принимает три различных значения: 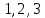 . . При этом значение 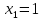 в выборке повторяется 12 раз, т.е. в выборке повторяется 12 раз, т.е. 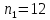 ; значение ; значение 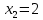 повторяется 3 раз и поэтому повторяется 3 раз и поэтому 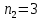 ; значение ; значение 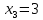 встречается 10 раз и встречается 10 раз и 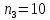 . .Составим статистическое распределение частот:
Построим полигон частот: 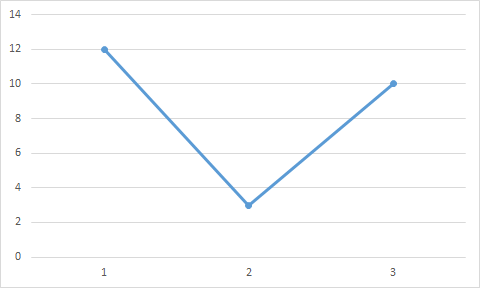 Найдем относительные частоты каждого значения и составим статистическое распределение относительных частот по формуле: 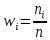 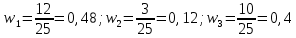
Построим полигон относительных частот: 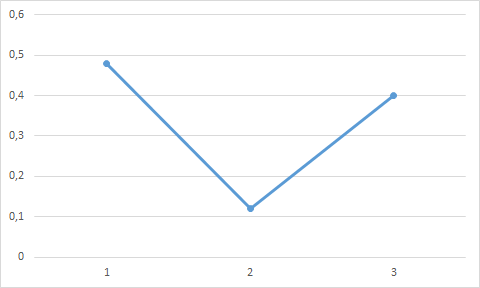 Найдем эмпирическую функцию распределения по формуле: 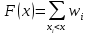 Используя данные таблицы, находим: 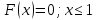 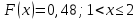 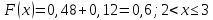 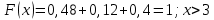 Таким образом, 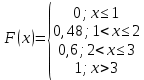 Построим график этой функции: 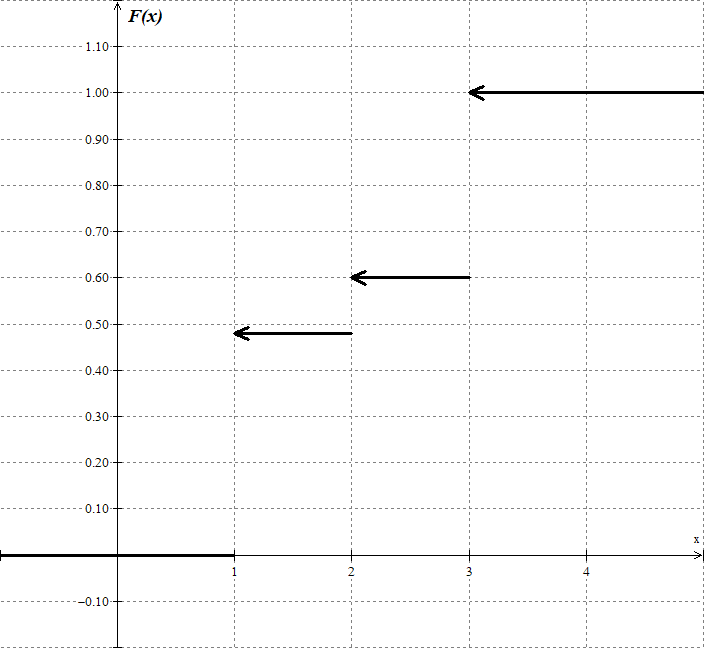 Выборочную среднюю 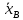 можно найти по формуле: можно найти по формуле: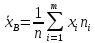 Используя данные таблицы, находим: 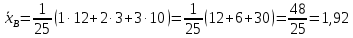 Выборочная дисперсия 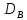 определяется равенством: определяется равенством: 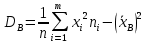 Найдем: 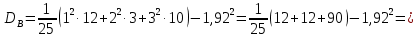 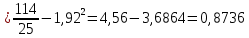 Выборочное среднее квадратическое отклонение: 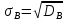 Следовательно, 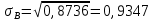 |