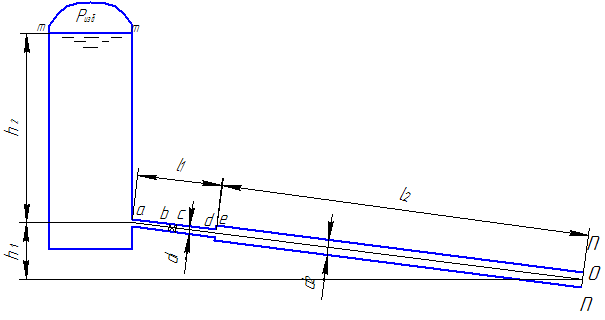
Расчет простого трубопровода. севастополь. Решение Так как по условию течение установившееся, используем уравнение Бернулли (2) и уравнение неразрывности (1)

• Название: Решение Так как по условию течение установившееся, используем уравнение Бернулли (2) и уравнение неразрывности (1)
• Анкор: Расчет простого трубопровода
• Дата: 13.09.2022
• Размер: 109 Kb.
• Имя файла: севастополь.doc
• Тип: Решение; #675775

Определить расход Q, избыточное давление в сечении с - с, построить диаграмму уравнения Бернулли простого трубопровода, считая уровень воды в резервуаре постоянным, абсолютную эквивалентную зернистую шероховатость равной к = 0,5 мм. Температура воды t= 15°C; р_изб= 196 гПа

h₁=3м l₁=20 м d₁=100мм

h₂=10м l₂=100м d₂=200мм

P_изб=196гПа
Решение

Так как по условию течение установившееся, используем уравнение Бернулли

(2)

и уравнение неразрывности

(1).

Ориентировочно полагаем, что режим течения турбулентный, поэтому коэффициенты a₁ и a₂ можно принять равными единице.

1.1. Расчет расхода жидкости.

a) Плоскость сравнения 0 - 0 проводим через наиболее низкую точку потока - через центр выходного сечения п - п.

b) Сечения выбираем так, чтобы в одном из них находились искомые величины, а в другом - максимум известных. Такими сечениями являются: сечение по поверхности воды в напорном баке m - m и сечение на выходе из трубопровода п - п.

c) Составляем таблицу значений z, p и v_cpдля этих сечений:

Сечение	z		P	v cp
m -m	H=h1+h2		Ратм + Ризб	0
n-n	0		Ратм	v2

Уравнение (2) с учетом значений z, р и v_cpпринимает вид

(3)

и показывает, что удельная потенциальная энергия воды в напорном баке



превращается в удельную кинетическую энергию



вытекающей струи и затрачивается на преодоление гидравлических сопротивлений


Далее выражаем потерю напора h_wчерез коэффициенты и скоростные напоры по участкам. В рассматриваемой задаче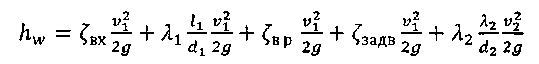

(4)

где

ζ_вх - коэффициент местного сопротивления при входе из бака в трубопровод;

λ₁и λ₂ - коэффициенты гидравлического трения на участках 1 и 2;

ζ_в.р - коэффициент местного сопротивления при внезапном расширении;

ζ_задв^_ коэффициент местного сопротивления в задвижке.

Скорости v₁и v₂связаны уравнением неразрывности (1)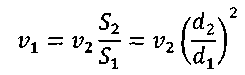



подставляя в уравнение (4) получим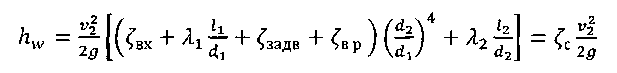

(5)

где выражение в квадратных скобках называется приведенным коэффициентом сопротивления трубопровода и обозначено как ζ_с.

Подставляя выражение (5) в уравнение (3) и решив относительно v₂ , окончательно получим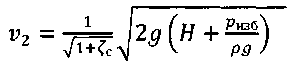

(6)

Искомый расход определится по формуле

(7)

Вычисления по формулам (6) и (7) затрудняются тем, что приведенный коэффициент потери напора трубопровода ζ_с в общем случае зависит от числа Re, т.е. от искомой скорости. Длярешения такого рода задач используем метод последовательных приближений. Задаём в первом приближении расход Q, по нему находим Re, λ и ζ и по формулам (5) - (7) определяют расход Q в следующем приближении.

В первом приближении примем режим, соответствующий квадратичному сопротивлению. Коэффициенты λ₁ и λ₂для него определим по формуле: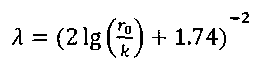



Тогда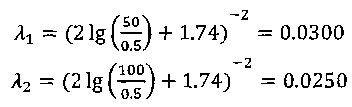



Коэффициент местной потери при входе оценим по формуле, приведенной в

приложении 2 для внезапного сужения потока. При S₂/S₁ → 0 получим



Коэффициент местной потери напора при переходе от диаметра d₁ к d₂определим по формуле из приложения 2 для внезапного расширения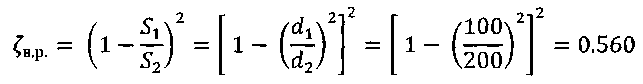



Коэффициент потери напора в задвижке ζ _задв при степени открытия 0.8 может быть принят равным, см. приложение 2:



После этого вычисляем приведенный коэффициент потери напора

⁼

По формуле (6) вычисляем скорость на участке 2: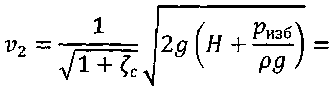





По формуле (7) вычисляем расход





Средние скорости и числа Рейнольдса по участкам при этом расходе равны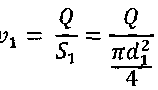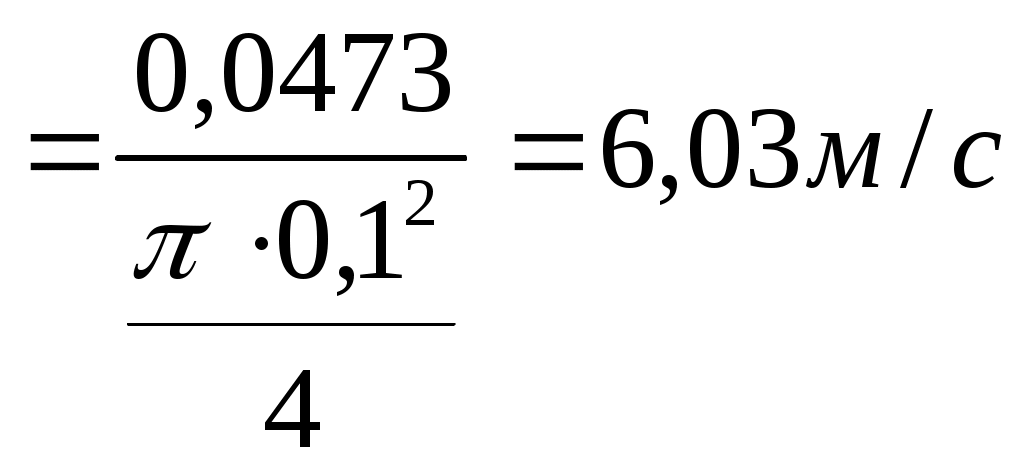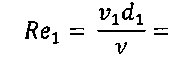













Определяем для второго приближения коэффициенты потери напора на трение λ по упрощенной формуле А.Д. Альтшуля, приняв k₁=0,1k=0.05мм: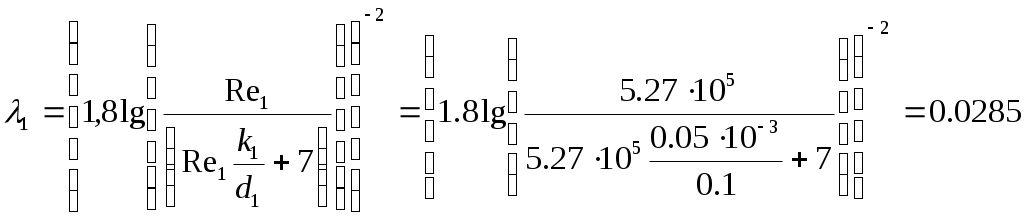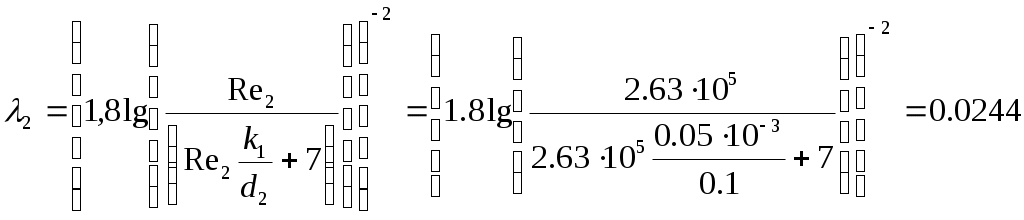




Значения λ₁ и λ₂ для второго приближения отличаются от соответствующих

коэффициентов первого приближения незначительно: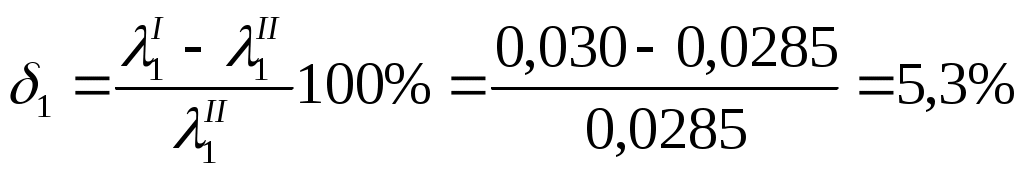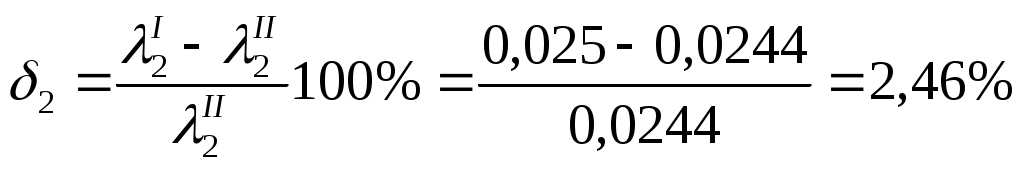





поэтому расчет для второго приближения не выполняем.
1.2. Расчет диаграммы уравнения Бернулли.

Для построения диаграммы вычислим скоростные напоры:





Вычислим потери напора для характерных сечений h_m,i=ζ_m,i h_{i ск} :

- сечение a – a, ζ_m,a=ζ_вх,

h_m,a= ζ_m,a h_ск1= 0,5х1,85=0,925м
- сечение b – b, ζ_m,b=ζ_вх+0.5 λ₁l₁/d₁,

h_m,b= ζ_m,b h_ск1=(0,50+0,5х0,030х20/0,1)1,85=6,475 м
- сечение c – c, ζ_m,c=ζ_вх+0.5 λ₁l₁/d₁ζ_задв,

h_m,c= ζ_m,c h_ск1= (0,50+0,5х0,030х20/0,1+0,20)1,85=6,845м
- сечение d-d,

(0.50 + 0.030х20/0,1 + 0.20)1.85 = 12,395 м,
- сечение е-е,

(0.50 + 0.030х20/0,1 + 0.20 + 0.56)1,85 = 13,431 м,
- сечение п - п,

h_m,n=ζ_mnh_ск2=((0,50+0,030х20/0,1+0,20+0,56)(0,20/0,10)⁴+0,025х100/0,2)0,116=

=14,925м
Проверяем точность результата, подставив численные значения h_mnи h_2tKв исходное уравнение (3)

13+ 2 - 0.116 – 14,925 = -0,041 м.

Погрешность около 0,27%, что соответствует точности исходных данных.

По рассчитанным значениям потерь напора строим диаграмму уравнения Бернулли, см. рис. 1. От уровня напора в баке

15,0 м

для каждого характерного сечения откладываем вниз потерю напора h_mlдо этого сечения. Получаем напорную линию 3. Отложив вниз от нее скоростные напоры, строим пьезометрическую линию 2. Геометрическая линия в рассматриваемом примере - наклонная прямая 4. На участках, где пьезометрическая линия выше геометрической, в трубопроводе давление больше атмосферного (до точки А на рис. 1) Там, где пьезометрическая линия ниже геометрической (от точки А до концевого сечения), в трубопроводе вакуум, т.е. давление меньше атмосферного. Расстояние между пьезометрической и геометрической линиями по вертикали для любого сечения равны избыточному давлению (или вакууму) в метрах столба движущейся жидкости. Для заданного по условию задачи сечения с - с (за задвижкой) (р — р_атм)_с 1 м вод. ст. ≈ 100 гПа