|
|
СОР 4 Координатная система. Решение текстовых задач Цель обучения
ЗАДАНИЯ ПО СУММАТИВНОМУ ОЦЕНИВАНИЮ ЗА 4 ЧЕТВЕРТЬ
Суммативное оценивание за раздел
«Прямоугольная система координат на плоскости»
Тема
|
Метод координат на плоскости
Решение текстовых задач
|
Цель обучения
|
8.1.3.14 вычислять расстояние между двумя точками на плоскости по их координатам
8.1.3.15 находить координаты середины отрезка
8.1.3.17 знать уравнение окружности с центром в точке (a,b) и радиусом r:(𝑥−𝑎)2 + (𝑦−𝑏)2 = 𝑟2
8.1.3.18 строить окружность по заданному уравнению
8.1.3.20 решение простейших задач в координатах
|
Критерий оценивания
|
Обучающийся
Применяет соотношения между координатами середины и координатами концов отрезка
Составляет уравнение окружности
Строит окружность по заданному уравнению
Решает простейшие задачи в координатах
|
Уровень мыслительных навыков
Время выполнения 25 минут
|
Применение
Навыки высокого порядка
|
Задания
1 вариант
Точка Т – середина отрезка МР. Найдите координаты точки Р, если
Т (-3;4) и М (-5; -7). 
2. а) АВ – диаметр окружности с центром О. Найдите координаты центра окружности, если А (7; -2) и В (-1;-4). [2]
В)Запишите уравнение окружности, используя условия пункта а. [2]
3. Дано: 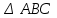 , , 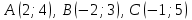 . Напишите уравнение медианы АМ. [3] . Напишите уравнение медианы АМ. [3]
4.Точки А(-4;-3), В(-4;5), С(2;5), D(8;-3) – вершины прямоугольной трапеции с основаниями ВC и АD. Найдите длину средней линии [3]
Схема выставления баллов
Критерий оценивания
|
№
задания
|
Дескриптор
|
Балл
|
Обучающийся
|
Применяет соотношения между координатами середины и коор-тами концов отрезка
|
1
|
выражает координаты конца отрезка через координаты середины и координаты другого конца отрезка
|
1
|
находит координаты точки
|
1
|
Составляет уравнение окружности
|
2а
|
выражает координаты середины отрезка через координаты его концов
|
1
|
находит координаты центра окружности
|
1
|
2b
|
определяет радиус окружности
|
1
|
записывает уравнение окружности
|
1
|
Записывает уравнение прямой
|
3
|
Находит координаты точки М
|
1
|
Записывает уравнение прямой, проходящей через две точки
|
1
|
Записывает уравнение искомой прямой
|
1
|
Решает простейшие задачи в координатах
|
4
|
находит координату середины одной боковой стороны или длину основания трапеции
|
1
|
находит координату середины второй боковой стороны или длину основания трапеции
|
1
|
находит среднюю линию
|
1
|
Всего баллов
|
|
|
12
|
Время выполнения
Задания
|
25 минут
2 вариант
|
Точка Т – середина отрезка МР. Найдите координаты точки Р,
если Т (-2;4) и М (-6; -7). 
2. a)АВ – диаметр окружности с центром О. Найдите координаты центра окружности, если А (9; -2) и В (-1;-6). [2]
b)Запишите уравнение окружности, используя условия пункта а). [2]
3. Дано: 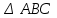 , , 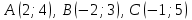 . Напишите уравнение медианы ВМ. [3] . Напишите уравнение медианы ВМ. [3]
4.Точки А(-3;-4), В(5;-4), С(5;8), D(-3;-1) – вершины прямоугольной трапеции с основаниями ВC и АD, АВ┴ ВС. Найдите среднюю линию трапеции. [3]
Схема выставления баллов
Критерий оценивания
|
№
задания
|
Дескриптор
|
Балл
|
Обучающийся
|
Применяет соотношения между координатами середины и коор-тами концов отрезка
|
1
|
выражает координаты конца отрезка через координаты середины и координаты другого конца отрезка
|
1
|
находит координаты точки
|
1
|
Составляет уравнение окружности
|
2а
|
выражает координаты середины отрезка через координаты его концов
|
1
|
находит координаты центра окружности
|
1
|
2b
|
определяет радиус окружности
|
1
|
записывает уравнение окружности
|
1
|
Строит окружность по заданному уравнению
|
3
|
строит первую окружность
|
1
|
строит вторую окружность
|
1
|
делает вывод о взаимном расположении двух окружностей
|
1
|
Решает простейшие задачи в координатах
|
4
|
находит координату середины одной боковой стороны или длину основания трапеции
|
1
|
находит координату середины второй боковой стороны или длину основания трапеции
|
1
|
находит среднюю линию
|
1
|
Всего баллов
|
|
|
12
| |
|
|
 Скачать 35.69 Kb.
Скачать 35.69 Kb.
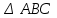 ,
, 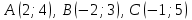 . Напишите уравнение медианы АМ. [3]
. Напишите уравнение медианы АМ. [3] 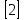
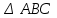 ,
, 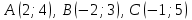 . Напишите уравнение медианы ВМ. [3]
. Напишите уравнение медианы ВМ. [3] 