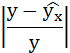физионометрика. Решение типовых задач Задача По территориям региона приводятся данные за 202 г. Таблица Исходные данные

• Название: Решение типовых задач Задача По территориям региона приводятся данные за 202 г. Таблица Исходные данные
• Анкор: физионометрика
• Дата: 25.03.2023
• Размер: 144.11 Kb.
• Имя файла: Zadaniya_dlya_prakticheskih_zanyatij_Parnaya_regressiya_i_korrel.docx
• Тип: Решение; #1014683
• страница: 2 из 4

4. Полученные оценки уравнения регрессии позволяют использовать его для прогноза.

5. Ошибка прогноза составит: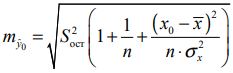

Задача 2. Имеются следующие данные разных стран об индексе розничных цен на продукты питания (х) и об индексе промышленного производства (у).

№ п/п	Индекс розничных цен на продукты питания (х)	Индекс промышленного производства (у)
1	100	70
2	105	79
3	108	85
4	113	84
5	118	85
6	118	85
7	110	96
8	115	99
9	119	100
10	118	98
11	120	99
12	124	102
13	129	105
14	132	112

Требуется:

1. Для характеристики зависимости у от х рассчитать параметры линейной регрессии.

2. Для каждой модели рассчитать показатели: тесноты связи и среднюю ошибку аппроксимации.

3. Оценить статистическую значимость параметров регрессии и корреляции.

Алгоритм решения:

1. Для расчёта параметров линейной регрессии



Решить систему нормальных уравнений относительно a и b: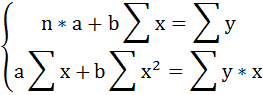



Построить таблицу расчётных данных, как показано в таблице 1.

Таблица 1 Расчетные данные для оценки линейной регрессии

№ п/п	х	у	ху	x 2	y 2
1	100	70
2	105	79
3	108	85
4	113	84
5	118	85
6	118	85
7	110	96
8	115	99
9	119	100
10	118	98
11	120	99
12	124	102
13	129	105
14	132	112
Итого:
Среднее значение:						х	х
			х	х	х	х	х
			х	х	х	х	х

Среднее значение определяет по формуле:

Реклама



Cреднее квадратическое отклонение рассчитывается по формуле: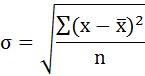



и заносится полученный результат в таблицу 1.

Возведя в квадрат полученное значение получим дисперсию: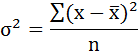



Параметры уравнения можно определить также по формулам: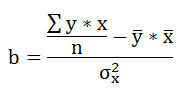





Подставить данные a и b в уравнение регрессии (см.пункт 1)

Рассчитать линейный коэффициент парной корреляции: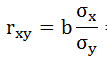



Определить коэффициент детерминации :
Рассчитать среднюю ошибку аппроксимации – среднее отклонение расчётных значений от фактических: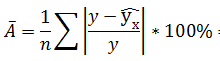



Оценка качества уравнения регрессии проводится с помощью F-теста.

F-тест состоит в проверке гипотезы Н₀ о статистической незначимости уравнения регрессии и показателя тесноты связи. Для этого выполняется сравнение фактического F_факт и критического (табличного) F_табл значений F-критерия Фишера.

F_факт определяется по формуле: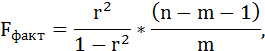



где n – число единиц совокупности;

m – число параметров при переменных х.

Задача 3. По 20 предприятиям региона изучается зависимость выработки продукции на одного работника (тыс.руб.) от ввода в действие новых основных фондов (% от стоимости фондов на конец года) и от удельного веса рабочих высокой квалификации в общей численности рабочих.

Требуется:

• 
  Построить линейную модель множественной регрессии. Записать стандартизированное уравнение множественной регрессии. На основе стандартизированных коэффициентов регрессии и средних коэффициентов эластичности ранжировать факторы по степени их влияния на результат.
  
• 
  Найти коэффициенты парной, частной и множественной корреляции. Проанализировать их.
  
• 
  Найти скорректированный коэффициент множественной детерминации. Сравнить его с нескорректированным (общим) коэффициентов детерминации.
  
• 
  С помощью – критерия Фишера оценить статистическую надежность уравнения регрессии и коэффициента детерминации 
  
• 
  С помощью частных – критериев Фишера оценить целесообразность включения в уравнение множественной регрессии фактора после и фактора после.
  
• 
  Составить уравнение линейной парной регрессии, оставив лишь один значащий фактор.
  

№	Y	X1	X2	№	Y	X1	X2
1	7	3.7	9	11	10	6.8	21
2	7	3.7	11	12	11	7.4	23
3	7	3.9	11	13	11	7.8	24
4	7	4.1	15	14	12	7.5	26
5	8	4.2	17	15	12	7.9	28
6	8	4.9	19	16	12	8.1	30
7	8	5.3	19	17	13	8.4	31
8	9	5.1	20	18	13	8.7	32
9	10	5.6	20	19	13	9.5	33
10	10	6.1	21	20	14	9.7	35