Электротехника задачи. Физика. Решение Угловую скорость находим как производную угла по времени Линейная скорость связана с угловой соотношением

• Название: Решение Угловую скорость находим как производную угла по времени Линейная скорость связана с угловой соотношением
• Анкор: Электротехника задачи
• Дата: 31.10.2021
• Размер: 274 Kb.
• Имя файла: Физика.doc
• Тип: Решение; #259765

1. Определить полное ускорение в момент времени t=3с точки, находящейся на ободе колеса радиусом 0,5м. Уравнение вращения колеса: , где А=2рад/c, В=0,2рад/с³.

Дано: ; ; ; ; .

Определить: .

Решение:

Угловую скорость находим как производную угла по времени :



Линейная скорость связана с угловой соотношением:



Угловое ускорение определяется первой производной от угловой скорости по времени ω′ или 2й производной от угла по времени φ″:



Тангенциальное ускорение связано с угловым соотношением:



По определению нормальное ускорение:



Полное ускорение определяется выражением:



Тогда с учетом вышеизложеных выражений получается:



Подставив числовые данные получим:



Ответ: Полное ускорение равно .
2. Тело скользит по наклонной плоскости, составляющей с горизонтом угол 45. Пройдя путь 36,4 см, тело приобретает скорость 2 м/с. Найти коэффициент трения тела о плоскость.

Дано: ; ; .

Определить: .

Решение: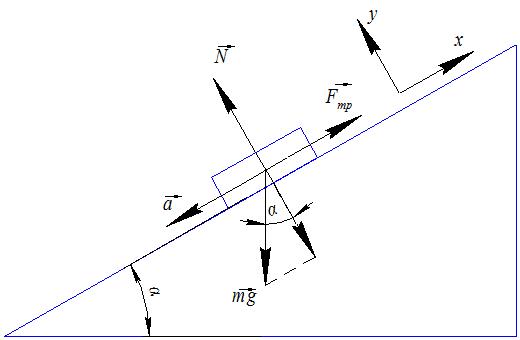



Рисунок – 2.1 – Схема движения тела по наклонной плоскости.

Согласно второму закону Ньютона:



где равнодействующая сила равна:



Проекция на ось х:



Проекция на ось y:



Сила трения:



Зависимость пути от времени для равноускоренного движения:


Из последней формулы можно определить ускорение:

Тогда второй закон Ньютона можно записать в виде:



Откуда можно определить коэффициент трения:





где - ускорение свободного падения.

Ответ: Коэффициент трения равен .


3. Ракета, масса которой вместе с зарядом 250г, взлетает вертикально вверх и достигает высоты 150м. Определить скорость истечения газов из ракеты, считая, что сгорание заряда происходит мгновенно. Масса заряда – 50 г.

Дано: ; ; .

Определить: .

Решение:

По закону сохранения импульса для системы «ракета-газ»:

, где

Откуда можно определить:



Закон сохранения энергии для ракеты:

, откуда
Сопоставив эти уравнения можно определить скорость истечения газов из ракеты: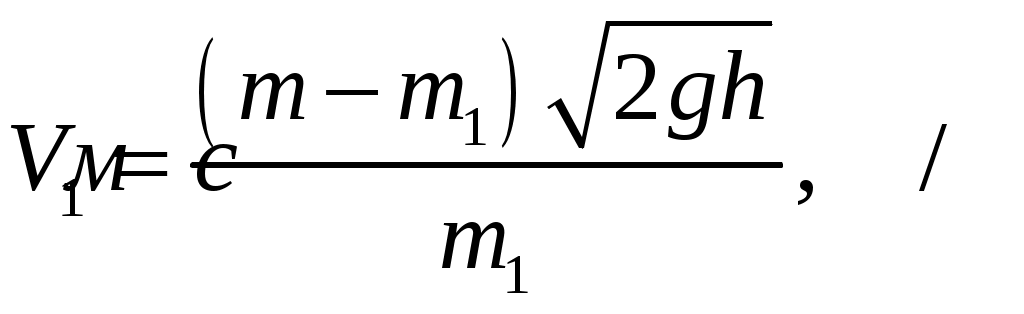





Ответ: Скорость истечения газов из ракеты .

4. Найти работу, которую надо совершить, чтобы увеличить скорость движения тела массой 10кг от 2м/с до 6м/с на пути 10м. На всем пути действует сила трения – 20Н.

Дано: ; ; ; ; .

Определить: .

Решение:

Часть совершенной работы пойдет на приращение кинетической энергии, а другая часть – на преодоление силы трения.



Работа, совершаемая на преодоление сил трения:



Тогда совершенная работа для увеличения скорости движения тела:





Ответ: Совершенная работа для увеличения скорости движения тела .

5. На барабан радиусом 0,5м намотан шнур, к концу которого привязан груз массой 10 кг. Найти момент инерции барабана, если известно, что груз опускается с ускорением 2,04м/с².

Дано: ; ; .

Определить: .

Решение: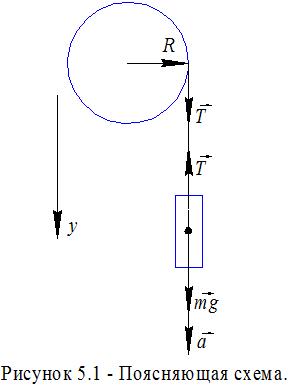




Согласно второму закону Ньютона:



Проекция на ось y:



Сила натяжения нити:



По определению момента силы:



Откуда момент инерции барабана:



Используя связь линейного и углового ускорений , можно определить:





где - ускорение свободного падения.

Ответ: Момент инерции барабана .

6. Кинетическая энергия вала, вращающегося вокруг неподвижной оси с постоянной скоростью, соответствующей частоте n=5 об/с, равна . Найти момент импульса вала.

Дано: ; .

Определить: .

Решение:

Момент импульса – вектор, направление которого по правилу векторного произведения равен: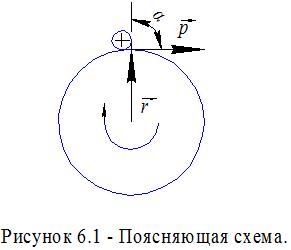



где , а модуль равен

, ,

Кинетическая энергия вала:

Момент инерции:

Угловая скорость:

Решая совместно эти уравнения можно получить:

, откуда

Тогда момент импульса вала равен:

;

Ответ: Момент импульса вала .