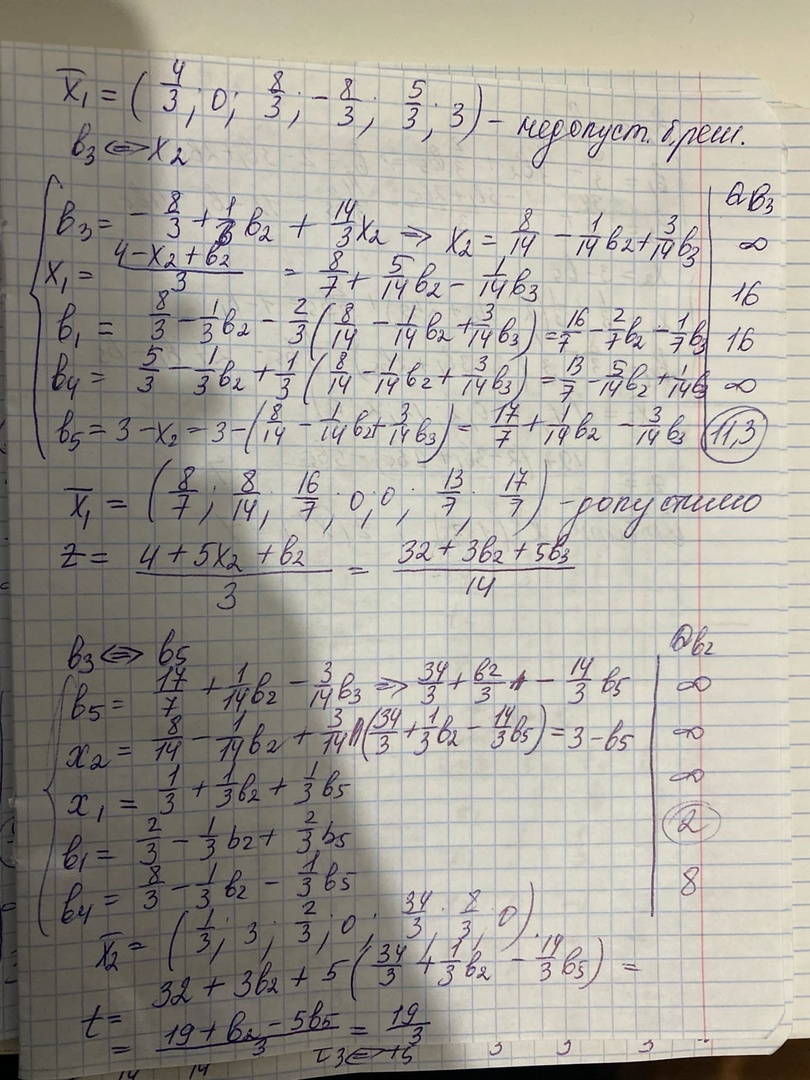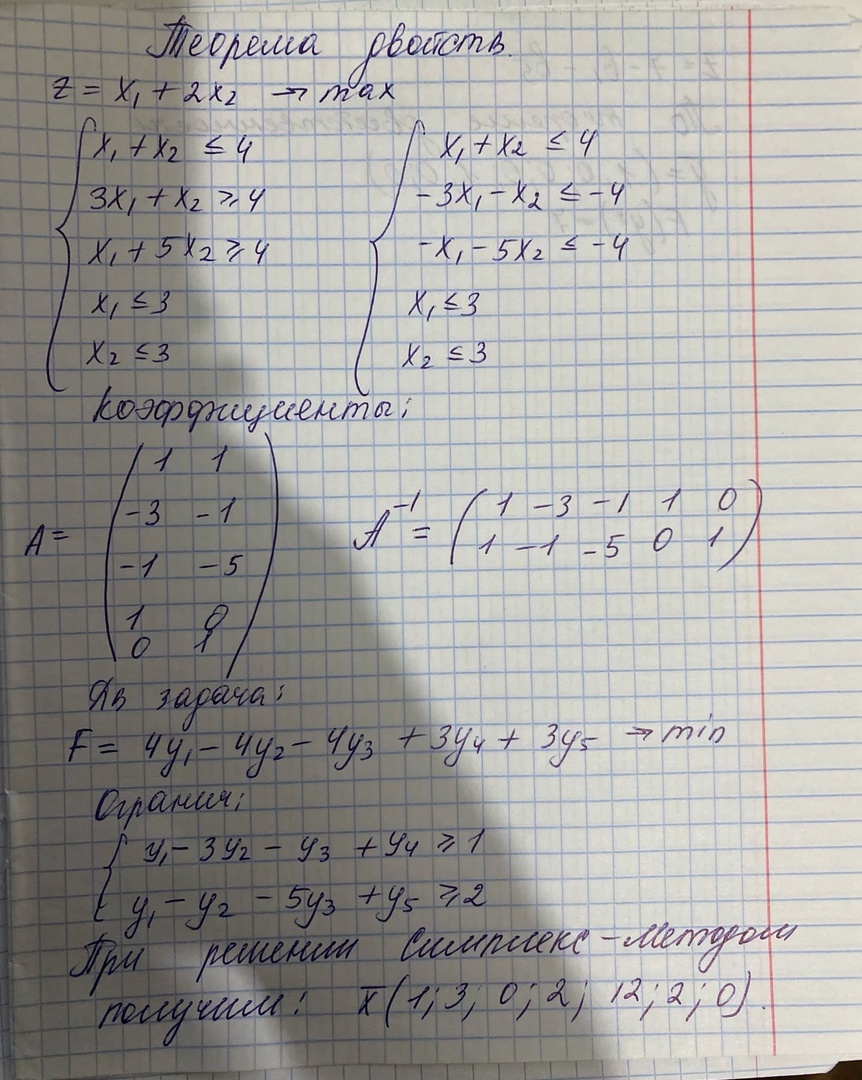|
|
Расчетно-графическая работа по Исследованию Операций Фомичева А.. Решение в Excel 11 Метод ветвей и границ 13 Метод Гомори 15 Решение двойственной задачи 16 Задание 2. 19
МИНОБРНАУКИ РОССИИ
|
Федеральное государственное бюджетное образовательное учреждение
высшего образования
«Нижегородский государственный архитектурно-строительный университет»
(ННГАСУ)
| институт технологий бизнеса Кафедра прикладной информатики и статистики Расчетно-графическая работа Вариант 10 Выполнил студент группы: ПИЭ-20.20 Фомичева А.С. Проверил доцент, к. физ.-мат. н.: Прокопенко Н.Ю. г. Нижний Новгород 2022 г СОДЕРЖАНИЕ
Задание №1. 3
Графический метод 3
Симплекс-метод 5
Табличный симплекс-метод 8
Решение в Excel 11
Метод ветвей и границ 13
Метод Гомори 15
Решение двойственной задачи 16
Задание №2. 19
Транспортная задача 19
Задание №3. 24
Теория игр 24
Задание №1.
Графический метод
Построим график наших ограничений. Отобразим на нем и направление градиента нашей функции.
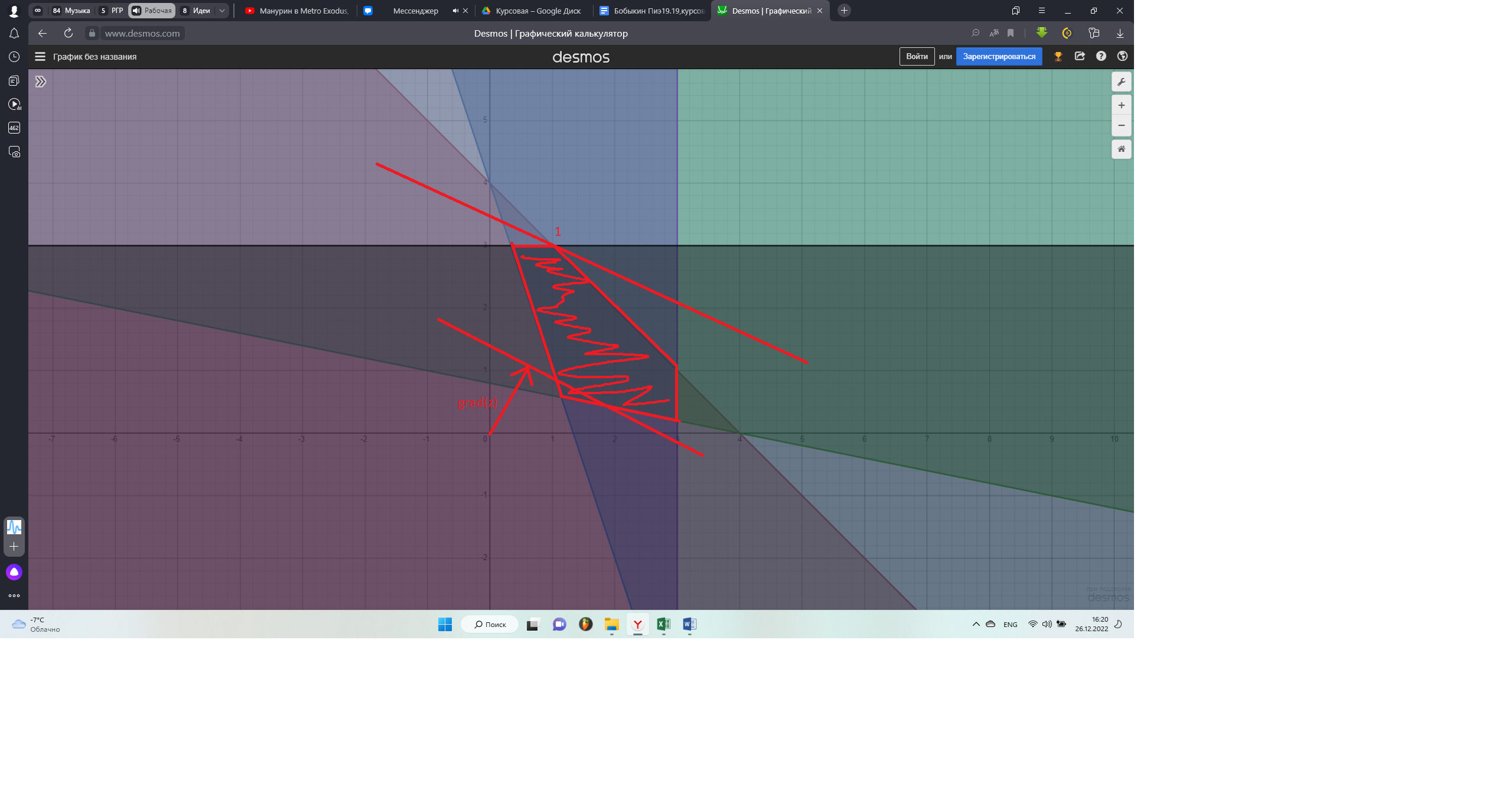

Симплекс-метод

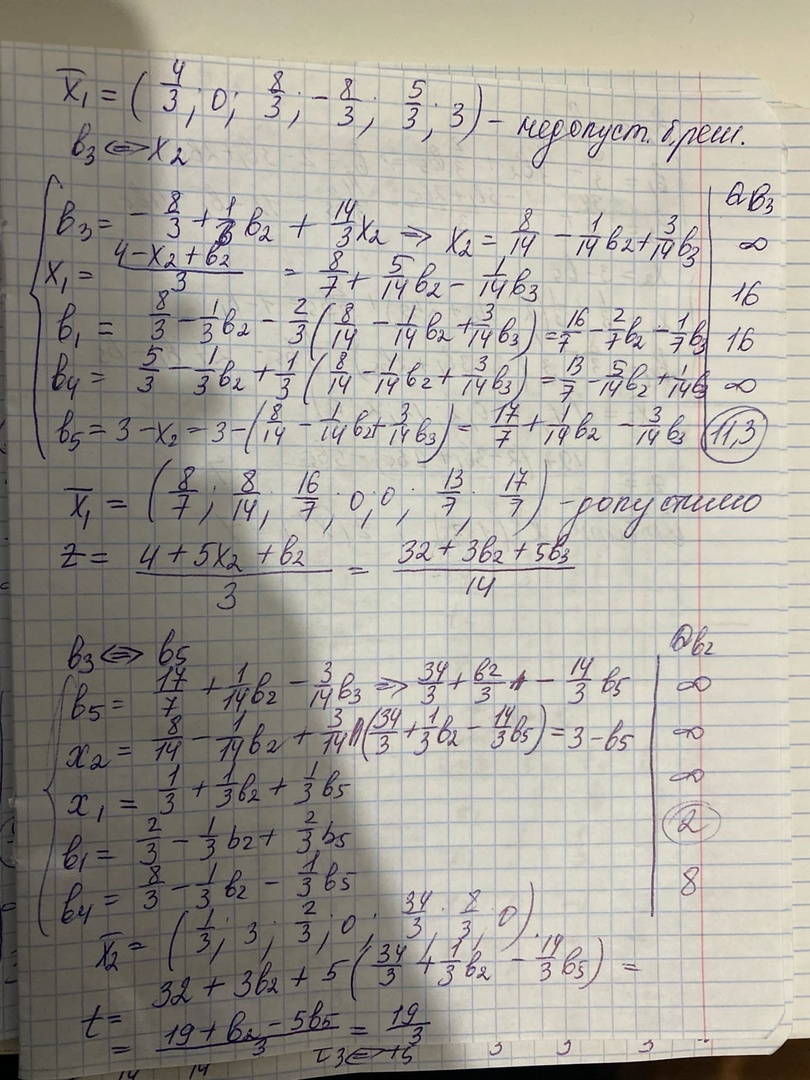

Табличный симплекс-метод
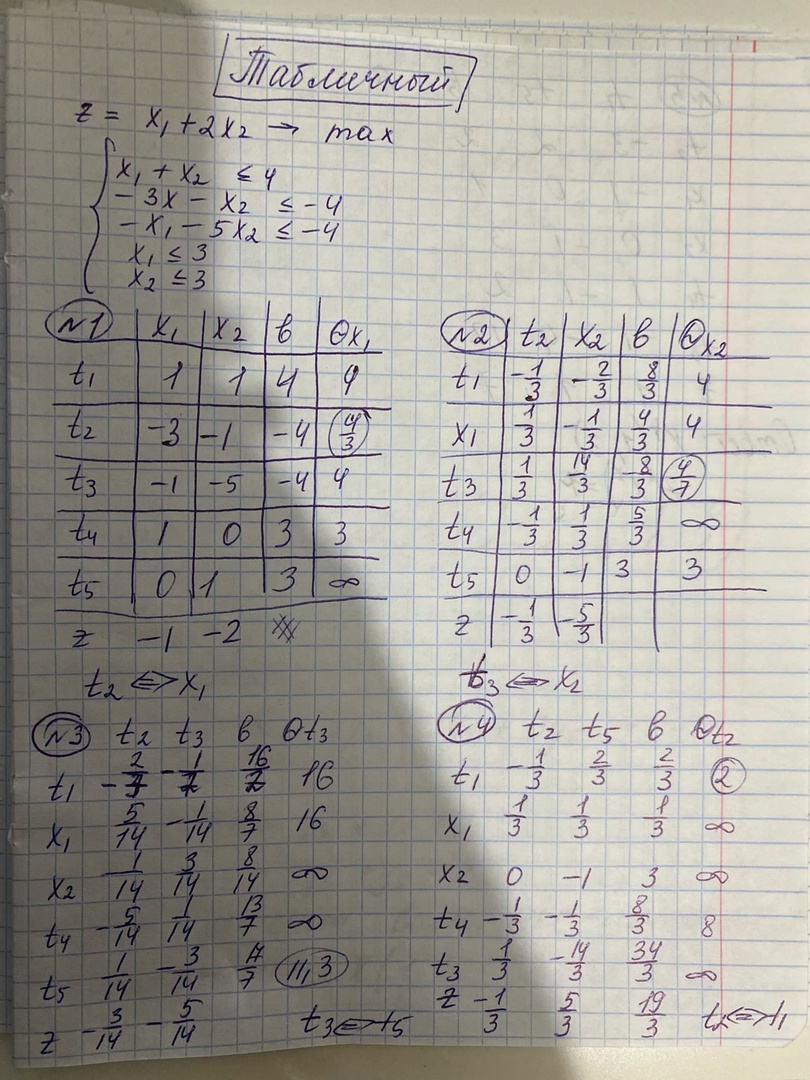

Решение в Excel
Введем наши данные в Excel и с помощью функции “Поиск решения” найдем решение нашей системы.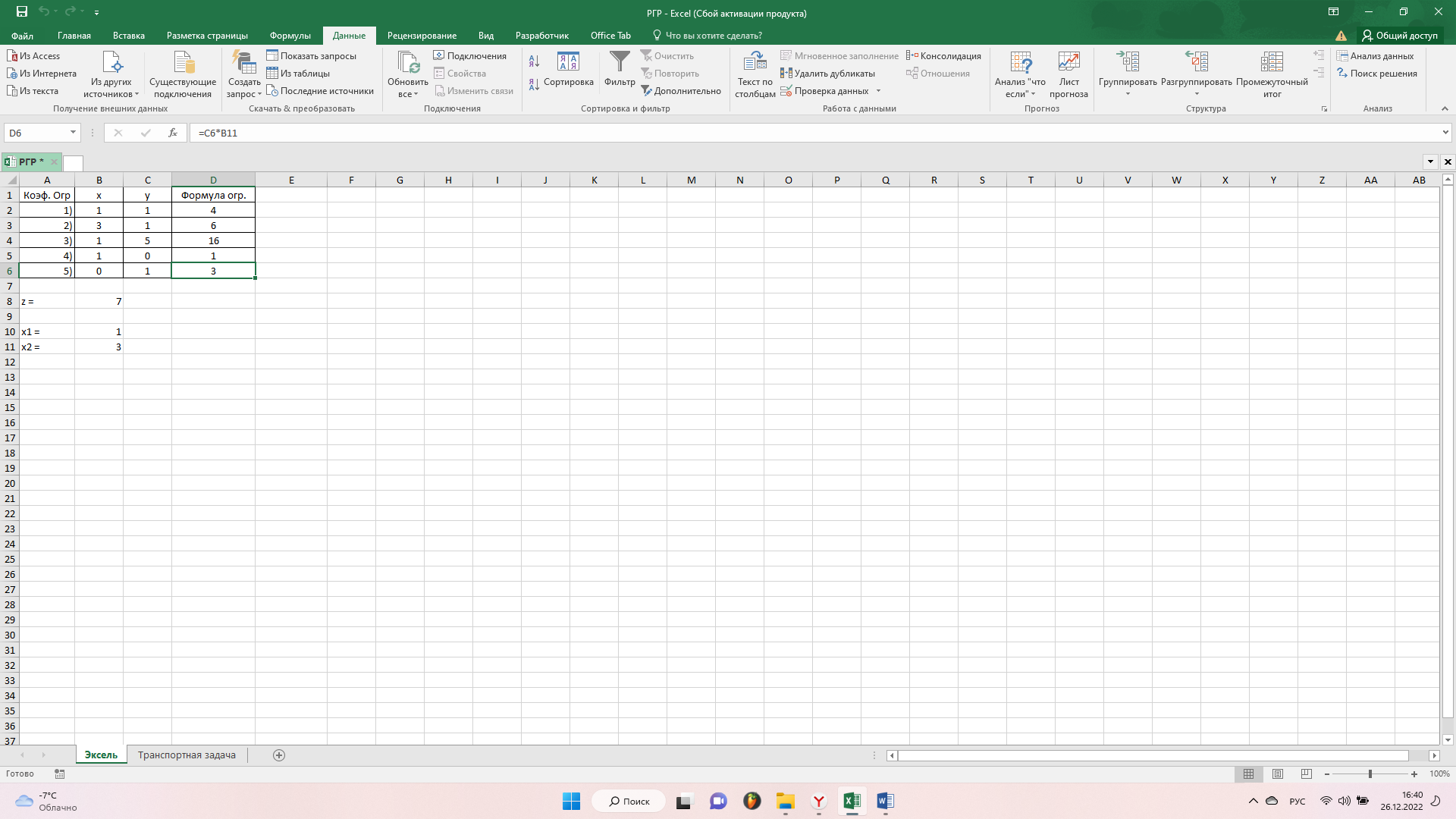
Метод ветвей и границ
Поскольку точка максимума данной функции и так является целочисленной, то решать данную задачу методом ветвей и границ не имеет смысла, поскольку данный метод используется для нахождения целочисленного решения.
Метод Гомори
Поскольку точка максимума данной функции и так является целочисленной, то решать данную задачу методом Гомори не имеет смысла, поскольку данный метод используется для нахождения целочисленного решения.
Решение двойственной задачи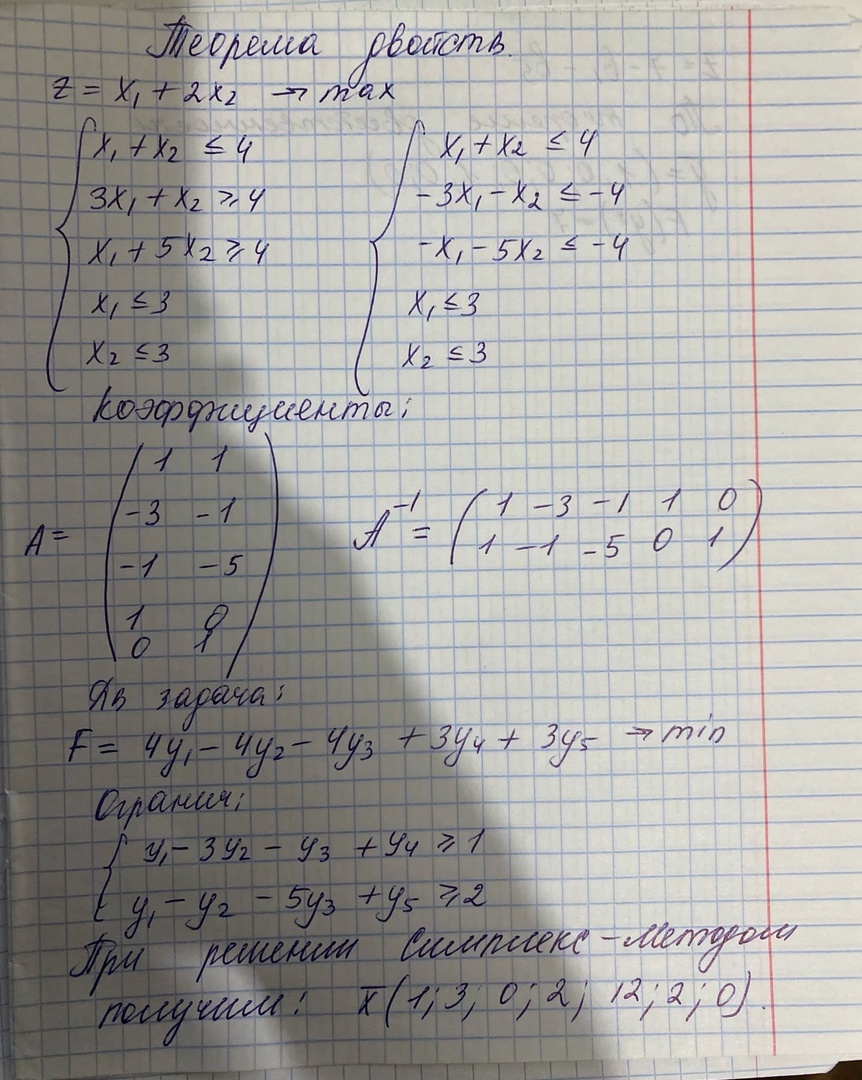

Задание №2.
Транспортная задача
Решать транспортную задачу будем в программе Excel для более удобного графического представления. Опорное решение найдем методом Северо-западного угла. Но для начала проверим необходимое условие решения нашей задачи.
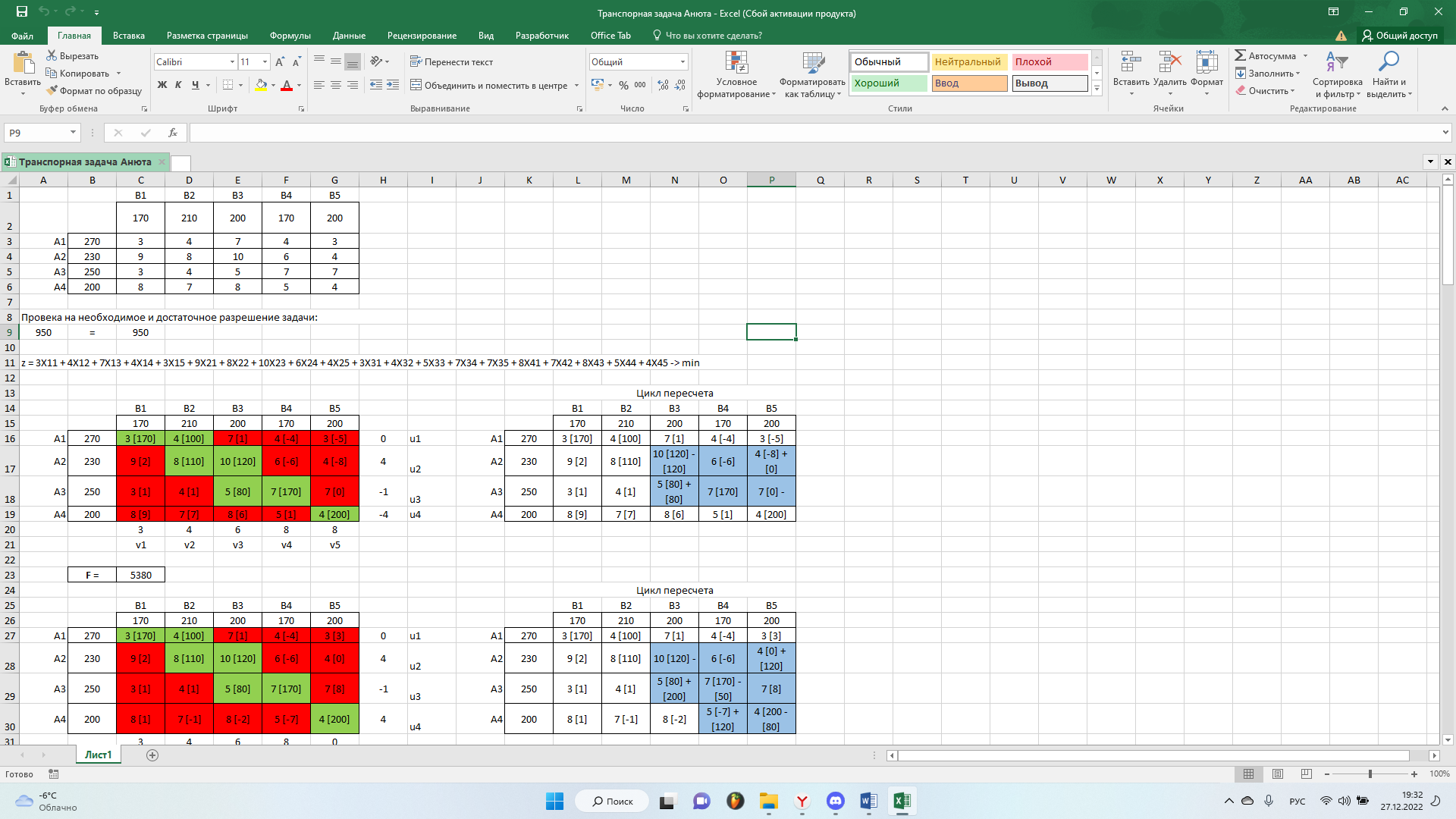
Запишем нашу функцию, которую необходимо минимизировать:
z = 3X11 + 4X12 + 7X13 + 4X14 + 3X15 + 9X21 + 8X22 + 10X23 + 6X24 + 4X25 + 3X31 + 4X32 + 5X33 + 7X34 + 7X35 + 8X41 + 7X42 + 8X43 + 5X44 + 4X45
Найдем опорное решение, теперь проверим результат на оптимальность, с помощью метода потенциалов:
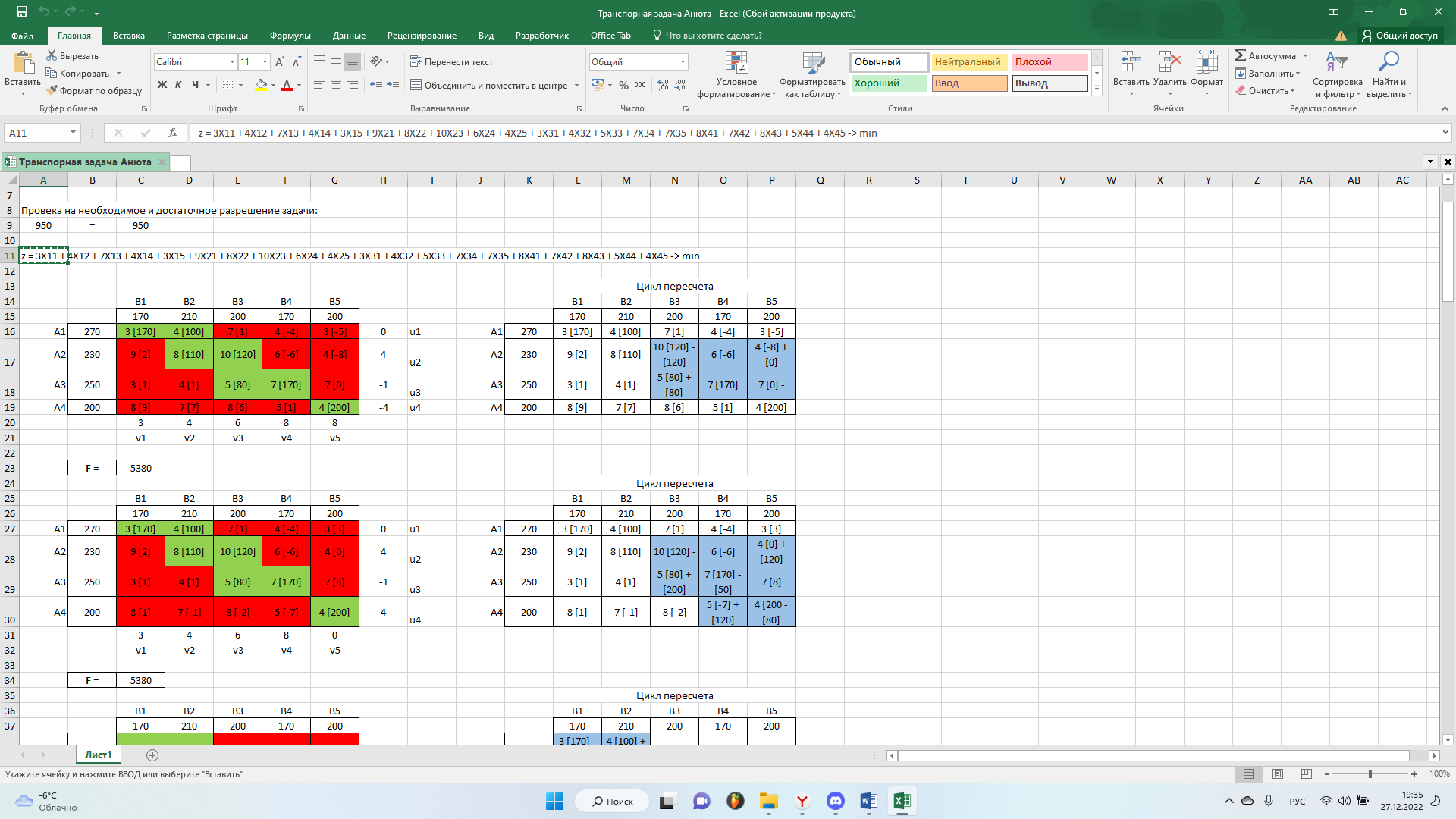
Как мы видим в матрице присутствуют отрицательные значения. Поэтому решение не оптимально. Далее, выполним цикл пересчета. Выберем наименьший отрицательный коэффициент:
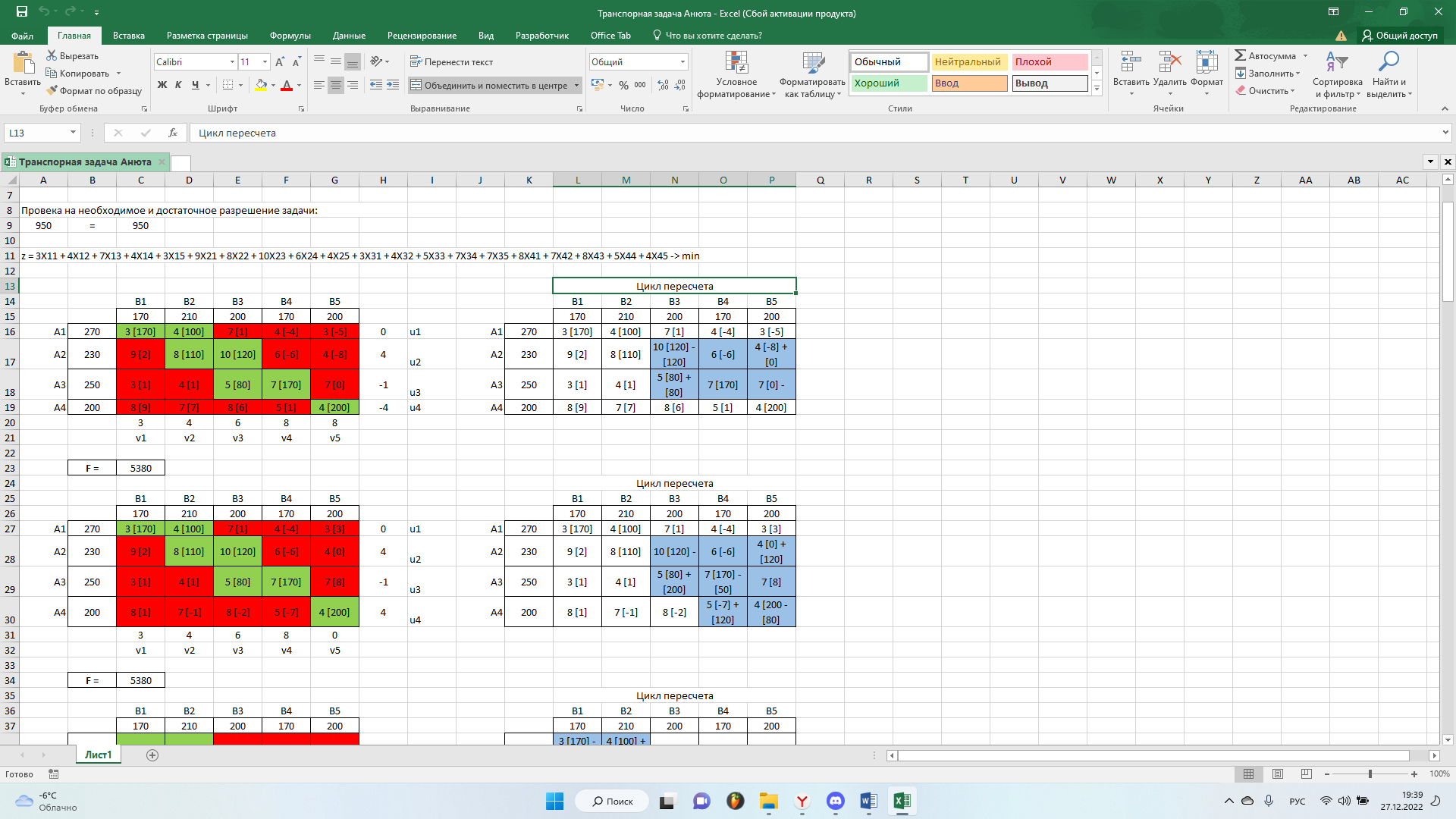
Двигаемся из последней ячейки второго ряда и создаем цикл пересчета. Из ячеек, где присутствует “-“, выбираем наименьшее значение Min(120, 0) = 0. Затем в ячейках, где стоит “+” прибавляем 0, там, где “–“ – отнимаем 6.
Получим новый опорный план:
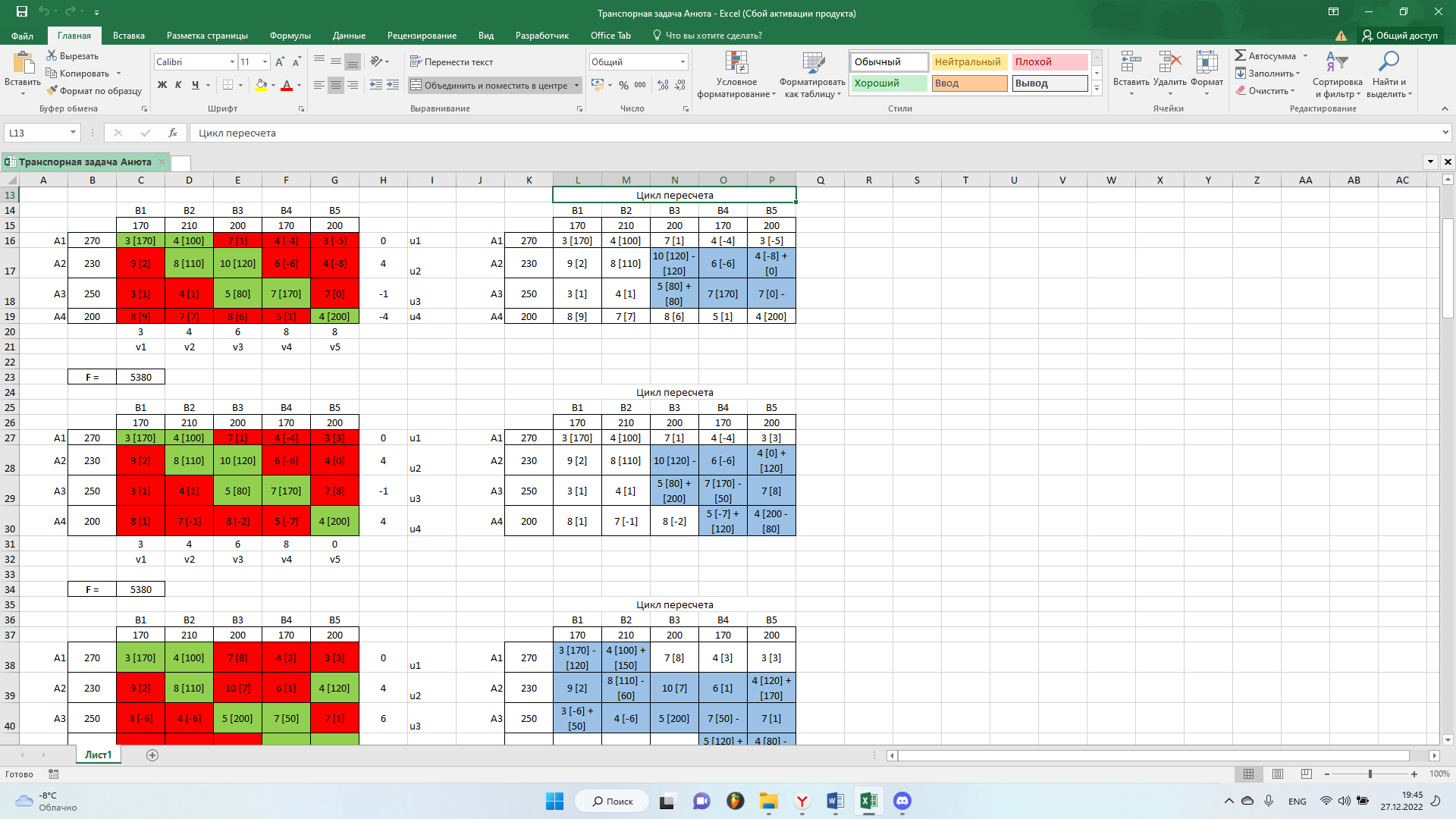
Как мы видим в матрице присутствуют отрицательные значения. Поэтому решение не оптимально. Далее, выполним цикл пересчета. Выберем наименьший отрицательный коэффициент:

Получим новый опорный план:
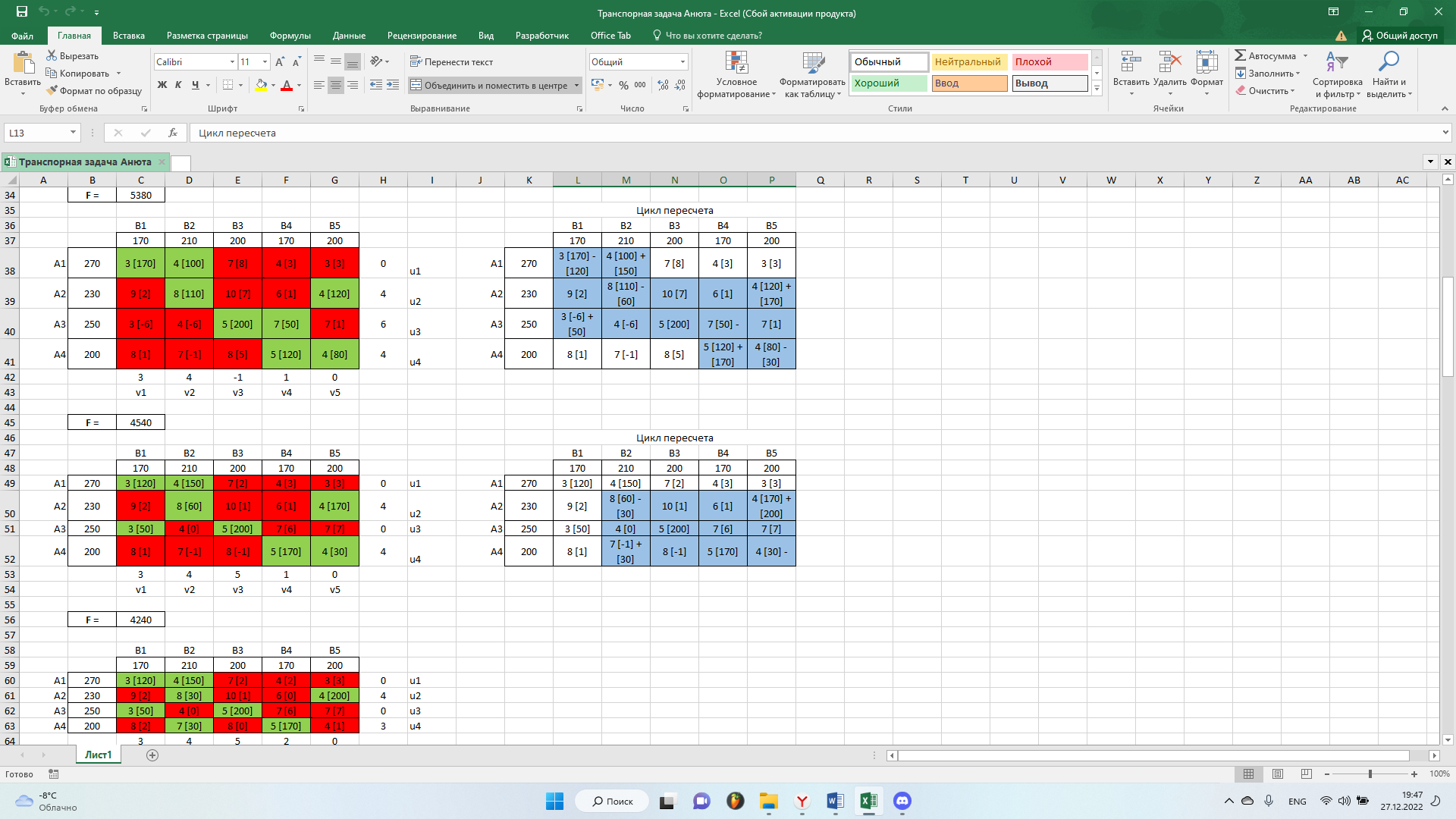
Как мы видим в матрице присутствуют отрицательные значения. Поэтому решение не оптимально. Далее, выполним цикл пересчета. Выберем наименьший отрицательный коэффициент:
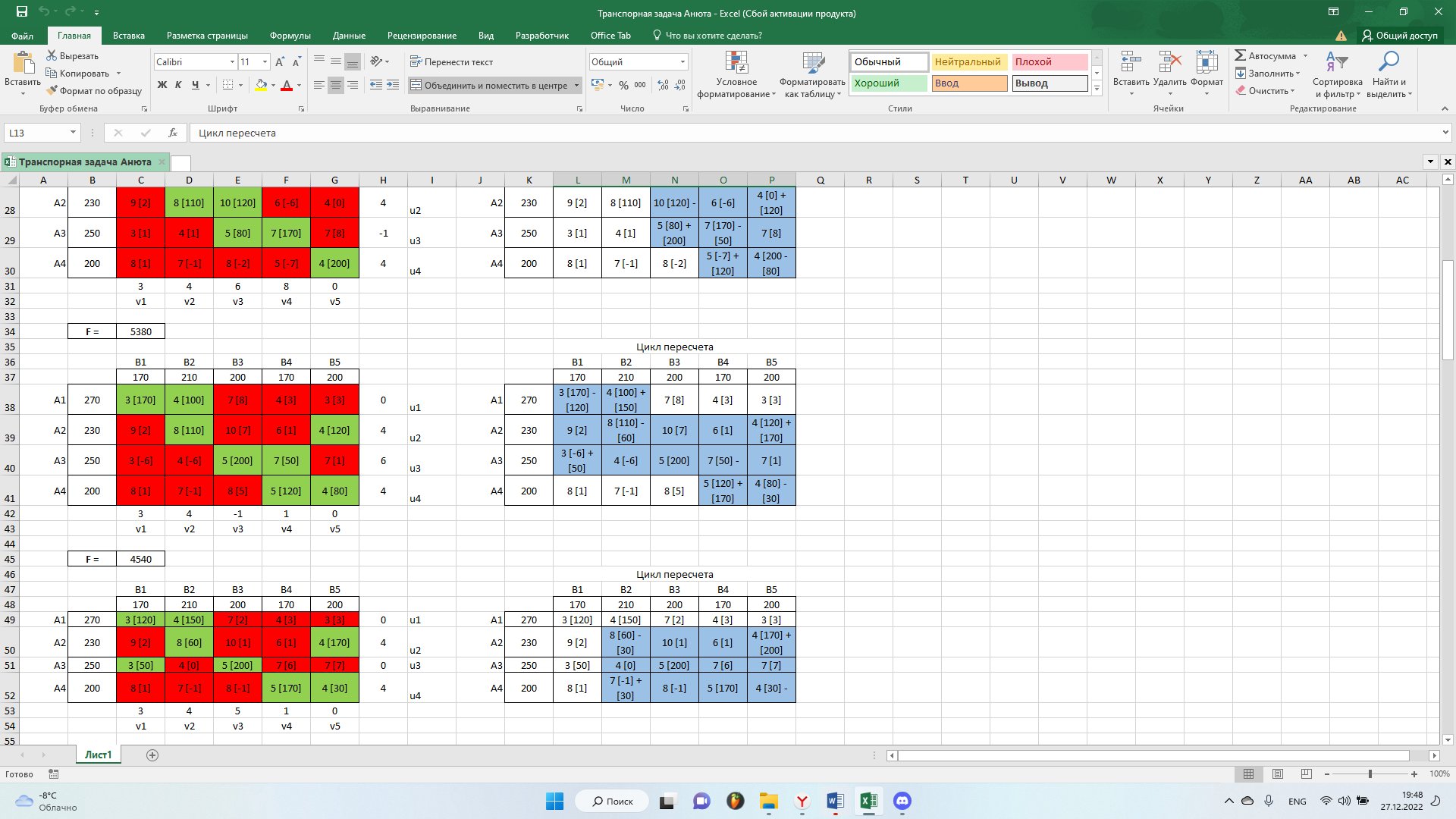
Получим новый опорный план:
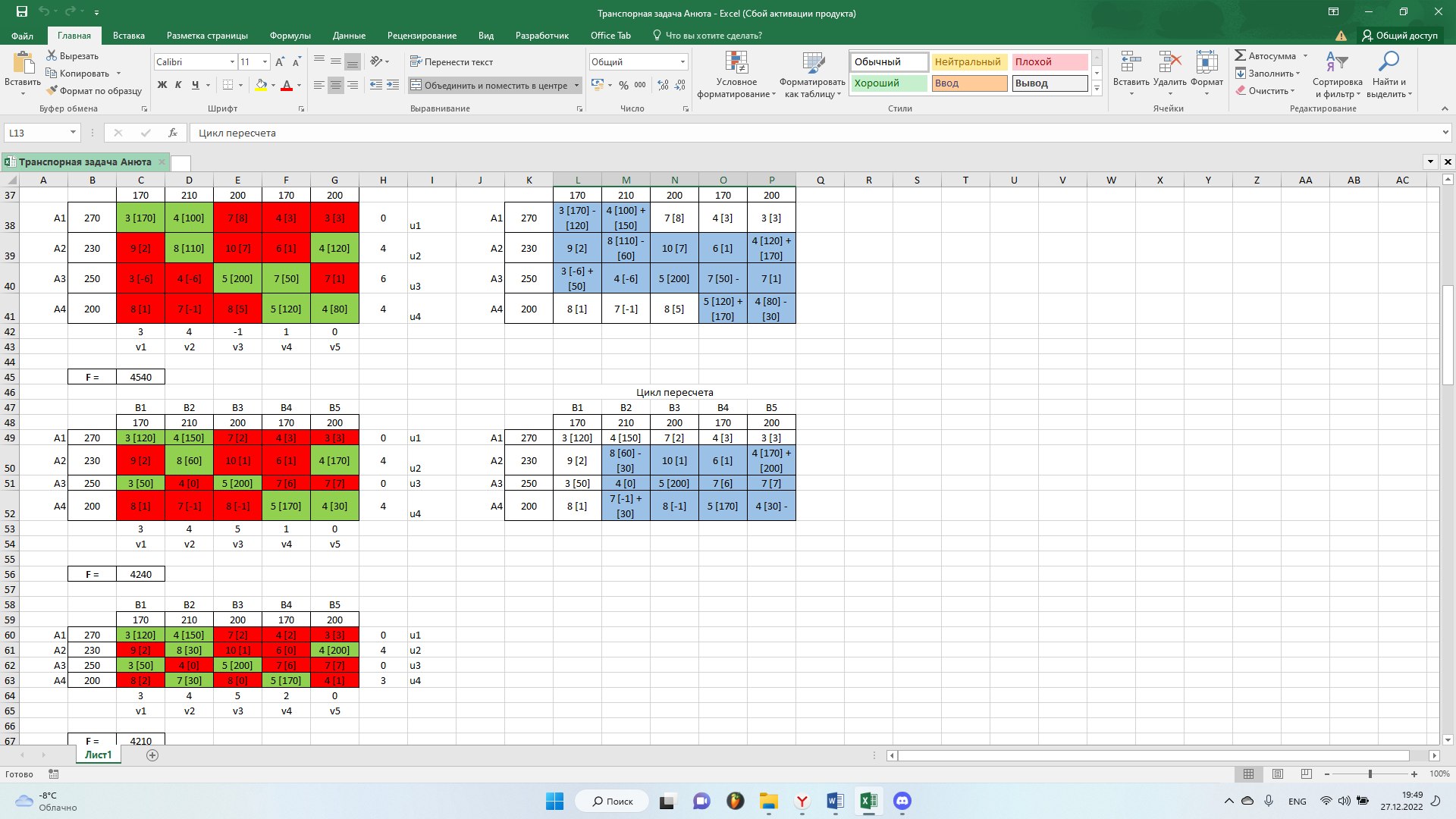
Как мы видим в матрице присутствуют отрицательные значения. Поэтому решение не оптимально. Далее, выполним цикл пересчета. Выберем наименьший отрицательный коэффициент:

Получим новый опорный план:
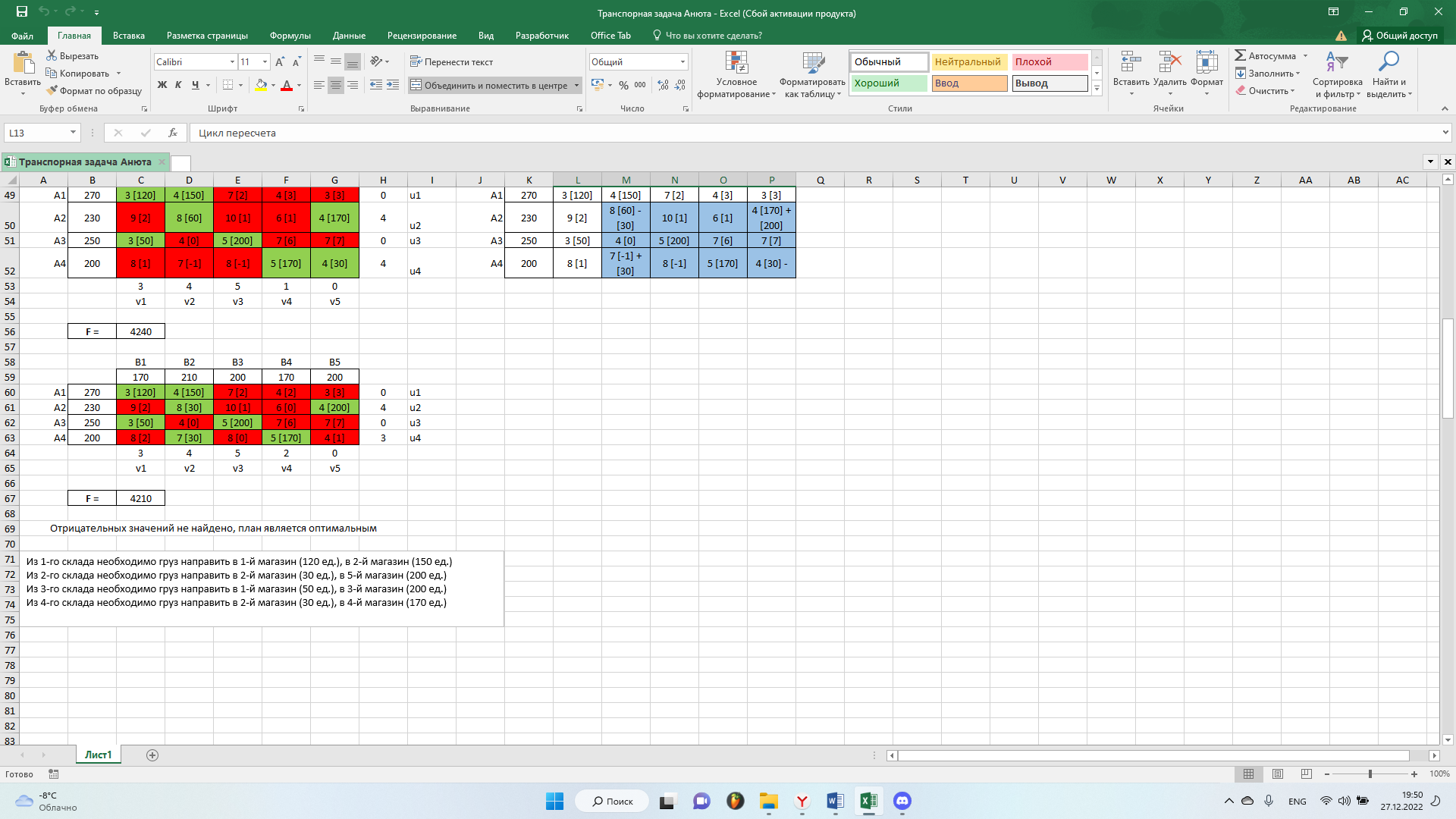
Отрицательных значений не найдено, план является оптимальным.
Из 1-го склада необходимо груз направить в 1-й магазин (120 ед.), в 2-й магазин (150 ед.).
Из 2-го склада необходимо груз направить в 2-й магазин (30 ед.), в 5-й магазин. (200 ед.).
Из 3-го склада необходимо груз направить в 1-й магазин (50 ед.), в 3-й магазин (200 ед.).
Из 4-го склада необходимо груз направить в 2-й магазин (30 ед.), в 4-й магазин (170 ед.).
Задание №3.
Теория игр
K1 K2 K3
П1 3 2 3
П2 1 5 5
П3 3 4 3
α = 3
β = 3
3<=v<=3
Значит цена игры (v) равна 3, следовательно, решение игры в чистых стратегиях. A(3;1) – седловая точка. |
|
|
 Скачать 4.45 Mb.
Скачать 4.45 Mb.