Лабораторная работа по теории надежности. Никишина Е.А. ver.2. Решение в исходной схеме элементы 10 11 и 12 образуют параллельное соединение. Заменяем их эквивалентным элементом для которого необходимо определить вероятность безотказной работы (вбр).
 Скачать 71.01 Kb. Скачать 71.01 Kb.
|
|
Министерство науки и высшего образования Российской Федерации ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ «Тюменский индустриальный университет» Институт геологии и нефтегазодобычи Кафедра кибернетически систем КОНТРОЛЬНАЯ РАБОТА по дисциплине «Надежность систем управления» «СТРУКТУРНО - ЛОГИЧЕСКИЙ РАСЧЕТ НАДЕЖНОСТИ ТЕХНИЧЕСКИХ СИСТЕМ» Вариант 4 Выполнил: студент гр. УТСбп(до)з-18-1 Никишина Е.А. Проверил: ст. препод. каф. КС Лапик Н.В. Тюмень 2023 Задание. Требуется в течение заданной наработки t=1200 ч определить показатели надежности системы по структурной схеме согласно варианту 4: - вероятность безотказной работы системы; - вероятность отказа системы; - γ-процентную наработку системы с вероятностью 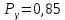 . .Дано: - элементы равно надежные с показателем надежности согласно варианту 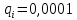 – вероятность отказа. – вероятность отказа.- режим работы всех элементов – нормальная эксплуатация; - на схеме 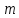 элементов, обведенные пунктиром, из элементов, обведенные пунктиром, из 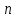 параллельных ветвей, являются минимально необходимыми для обеспечения работоспособности. параллельных ветвей, являются минимально необходимыми для обеспечения работоспособности.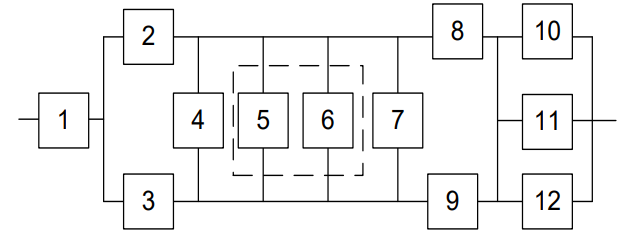 Рисунок 1 – Структурная схема надежности Решение: В исходной схеме элементы 10; 11 и 12 образуют параллельное соединение. Заменяем их эквивалентным элементом 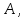 для которого необходимо определить вероятность безотказной работы (ВБР). Учитывая, что для которого необходимо определить вероятность безотказной работы (ВБР). Учитывая, что 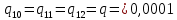 , получим: , получим: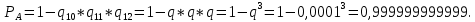 В результате первого этапа преобразований получаем схему, изображенную на рисунке 2. 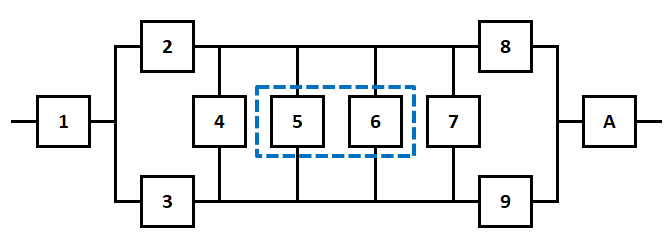 Рисунок 2 – Преобразованная на первом этапе схема В свою очередь, элементы 4, 5, 6 и 7 представляют собой подсистему «2 из 4». Заменим их на эквивалентный элемент 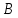 . ВБР такой подсистемы рассчитывается по биномиальному закону c учетом того, что . ВБР такой подсистемы рассчитывается по биномиальному закону c учетом того, что 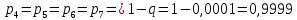 : :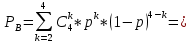 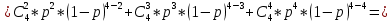 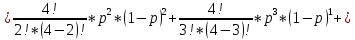 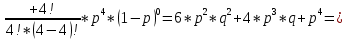 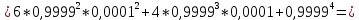 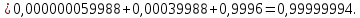 В результате второго этапа преобразований получаем схему, изображенную на рисунке 3. 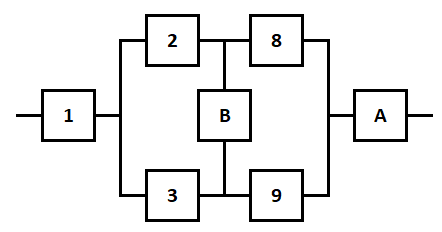 Рисунок 3 – Преобразованная на втором этапе схема В схеме по рисунку 3 элементы 2, 3, 8, 9 и элемент 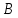 образуют мостиковую схему. Для ее расчета в качестве базового элемента выбираем диагональный элемент образуют мостиковую схему. Для ее расчета в качестве базового элемента выбираем диагональный элемент 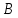 . При . При 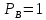 мостиковая схема превращается в параллельно-последовательное соединение (рисунок 4, а), а при мостиковая схема превращается в параллельно-последовательное соединение (рисунок 4, а), а при 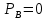 – в последовательно-параллельное (рисунок 4, б). – в последовательно-параллельное (рисунок 4, б).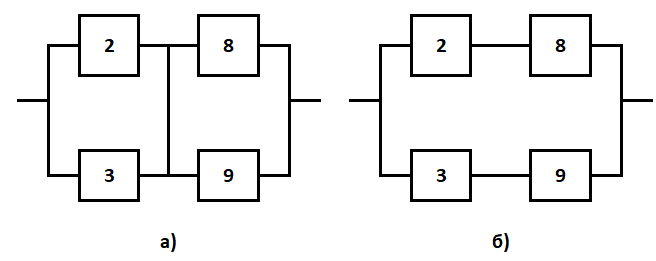 Рисунок 4 – Преобразование мостиковой схемы при работоспособном (а) и отказавшем (б) базовом элементе Тогда для схемы «короткое замыкание» для ВБР можно записать: 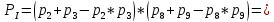 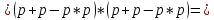 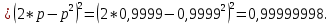 Соответственно для схемы «разрыв цепи» справедлива следующая запись для ВБР: 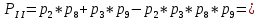 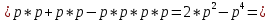 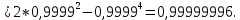 Здесь было учтено: 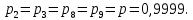 В результате мостиковая схема заменяется эквивалентным элементом 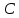 , ВБР для которого определяется следующим образом: , ВБР для которого определяется следующим образом: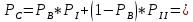 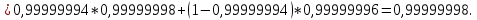 Окончательно получаем следующую расчетную схему: 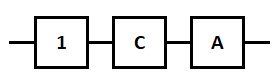 Рисунок 5 – Окончательная расчетная схема В схеме по рисунку 5 имеет место последовательное соединение трех элементов. Поэтому ВБР всей рассматриваемой системы в целом будет равна: 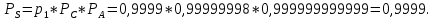 Соответствующая вероятность отказа системы будет равна: 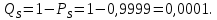 Так как все элементы системы находятся в режиме нормальной эксплуатации, то их ВБР подчинены экспоненциальному закону распределения, и значит, интенсивность отказов системы можно определить следующим образом: 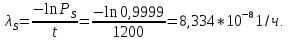 Гамма-процентная наработка на отказ системы определяется выражением: 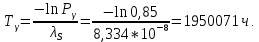 Ответ: вероятность безотказной работы системы – 0,9999, вероятность отказа – 0,0001. Данная система проработает безотказно с вероятностью 0,85 в течение 1950071 часа. СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ 1. Половко А.М.. Гуров С.В. Основы теории надежности. [Текст] - 2- е изд., перераб. и доп.- СПб.: БХВ- Петербург, 2006. 2. Бржозовский Б.М. Диагностика и надежность автоматизированных систем [Текст]: учебник для студентов вузов, обучающихся по направлению подготовки дипломированных специалистов "Автоматизированные технологии и производства"/авт., ред.Б. М.Бржозовский [и др.]; ред. Б. М. Бржозовский. - 3-е изд., перераб. и доп. - Старый Оскол : ТНТ, 2012. 3. Синопальников В.А. Надежность и диагностика технологических систем [Текст] /учебник для студентов вузов/ В. А. Синопальников, С. Н. Григорьев. - М.: Высшая школа, 2005. 4. Дианов В.Н. Диагностика и надежность автоматических систем: Учебное пособие. 2-е изд., стереотипное. – М.:МГИУ, 2005. 5. Половко А.М.. Гуров С.В. Основы теории надежности. Практикум. [Текст]- СПб.: БХВ - Петербург, 2006. |
